Методические указания. При выполнении курсовой работы необходимо:
При выполнении курсовой работы необходимо:
1. Привести примеры авиационного оборудования, в котором применяют следящие системы; 2. Описать работу исследуемой системы и составить функциональную схему; 3. Составить линеаризованное дифференциальное уравнение двухфазного асинхронного двигателя с короткозамкнутым ротором, определить передаточные функции его по управляющему и возмущающему воздействиям, определить параметры и построить структурную схему; 4. Записать линеаризованное уравнение остальных элементов системы и определить их передаточные функции; 5. Составить структурную схему системы; 6. Определить передаточную функцию разомкнутой системы; 7. Определить передаточные функции замкнутой системы относительно управляемой величины по задающему в возмущающему воздействиям; 8. Определить передаточные функции замкнутой системы относительно ошибки и возмущающему воздействиям; 9. Определить устойчивость системы без тахогенератора по критерию Гурвица; 10. Определить критическое или граничное значение коэффициента передачи тахогенератора; 11. Определить установившуюся ошибку замкнутой следящей системы при коэффициенте тахогенератора равном 5Ктг граничное; 12. Определить запас устойчивостисистемы при коэффициенте тахогенератора, равном 5Кт граничное; 13. Определить параметры системы, при которых запасы устойчивости соответствуют требованиям руководящих элементов; 14. Определить параметры системы, при которых величина перерегулирования и время регулирования будут минимальными 15. Построить график переходной характеристики и по нему определите показатели качества системы.
Пример расчета
Составляя уравнение асинхронного двигателя, следует учесть, что переходные процессы в обмотке управления протекают значительно быстрее, чем переходные процессы, характеризующие частоты вращения ротора. В связи с этим дифференциальное уравнение асинхронного двигателя в основном определяется на основании второго закона Ньютона для вращательного движения: Jпр где Jпр - момент инерции всех вращающихся масс, приведенный к валу двигателя. Jпр = J∂в + Ω∂ в - частота вращения вала двигателя; Мв р - вращающий момент; М´н - момент нагрузки, приведенный к валу двигателя и равный Мн/ηι; J∂ в - момент инерции двигателя; Jн - момент инерции нагрузки; ι - передаточное число редуктора; ρ - КПД редуктора.
Вращающий момент создается вращающимся магнитным полем и в общем случае аналитическое выражение для него будет достаточно сложным. Можно записать, что он является функцией напряжения, приложенного к обмотке управления uу, и частоты вращения двигателя Ω∂ в, т.е. Мв р = Мв р (uу, Ω∂ в). Экспериментальным путем получены зависимости Мвр = f1 (uу) и Mвр = f2 (Ω∂в) при Ω∂в= const при uу= const (рис. 2 и 3).
Для установившегося режима Jпр Под действием малых возмущений переменные двигателя отклоняются от установившегося режима на малые величины ΔΩ∂ в, Δuу и уравнение двигателя записывается в виде Jпр Нелинейность для вращающего момента можно разложить в ряд Тейлора и, пренебрегая членами второго и высшего порядка можно записать Мвр = Мвр (uу0, Ω∂ в 0) + Ω∂ в = Ω∂В0 uу = uу0 uу = uу0 Ω=Ω∂ в0 Частные производные момента определяются из рис.3,4 как тангенсы угла наклона касательных, проведенных и соответствующим кривым:
uу = uу0 Ω∂ в= Ω∂ в0 Ω∂ в= Ω∂ в0 uу = uу0 где Cu и Cp определяются параметрами двигателя и обычно задаются. Вычитая из уравнения для двигателя выражение установившегося режима, получаем линеаризованное уравнение: Jпр Разделив все члены уравнения на Ср Сu, будем иметь
Введем обозначения
и окончательно получим линеаризованное дифференциальное уравнение асинхронного двигателя: Т∂в Если выходной величиной двигателя считать угол поворота то учитывая, что ΔΩ∂в= Т∂в Применив преобразование Лапласа, будем иметь следующее алгебраическое уравнение: (Т∂в Р +1) Р φ∂в (Р) = К∂ uу (Р) - Кf М'н (Р)
Из этого уравнения получим передаточные функции двигателя по управлению возмущению W1(P) = W2(P) = Зная передаточные функции, можно построить структурную схему двигателя. Линеаризованное уравнение усилителя зависит от его типа. В курсовой работе уравнение усилителя рекомендуется записать в виде Tу где uу - выходноенапряжение, а Δu1 -входное напряжение.Затем так же, как и для двигателя, следуетполучить выражение передаточной функции. Уравнение для СКВТ, работающих в трансформаторном режиме при малых отклонениях, следует записать в виде uу = К1 (α – β). Выражение для тахогенератора можно, записать в виде uт г = Кт г ΔΩ∂ в, а для редуктора — в виде ΔΩред = После этого можно получить передаточные функции, а затем построить структурную схему следящей системы. Используя правила преобразования структурных схем, получаем все необходимые передаточные функции системы. Критический коэффициент передачи тахогенератора определяют из условия нахождения замкнутой системы на границе устойчивости. Для этого можно воспользоваться критерием Гурвица. Для определения установившейся ошибки следящей системы следует воспользоваться формулой qуст = ℓιm q (t) =ℓιm При этом q (р) = W1 (р) a(р) + W2 (р) М¢н (р) где W1 (р) ‑ передаточная функция замкнутой скорректированной системы относительно ошибки по задающему воздействию, a W2 (р) по возмущающему воздействию: a(p) = Для определения запаса устойчивости системы следует построить АФХ разомкнутой скорректированной (при 5Ктг граничное) системы. График переходной характеристики может быть построен как решение дифференциального уравнения при заданном воздействии в виде единичной ступенчатой функции и нулевых начальных условиях. При этом можно пользоваться классическим методом, преобразованием Лапласа, приближенными методами или аналогичными или цифровыми вычислительными машинами. Приведем методику расчета кривой переходной характеристики на ПВМ. Дифференциальное уравнение исследуемой электромеханической следящей системы имеет вид α0 где коэффициенты αί и в0 имеют численное значение для каждого варианта. Для расчета переходной характеристики задающее воздействие является единичным скачком, т.е. α(t) = 1(t) и начальные условия нулевые. Распространенным методом решения дифференциальных уравнений является их численное интегрирование. Получаемое при этом решение представляет собой последовательность дискретных значений частного интеграла уравнения. Численное интегрирование осуществляется с применением ЦВМ. Для этого дифференциальное уравнение высокого порядка (в нашем случае третьего) необходимо представить в форме нормальной системы уравнений первого порядка (форме Коши). В нормальных системах каждое уравнение разрешено относительно входящей в него производной первого порядка. Для рассматриваемой следящей системы уравнения в форме Коши принимают вид:
где: у1 = β; х = α После этого на алгоритмическом языке составляется программа интегрирования в заданном интервале времени с использованием одного из численных методов. В работе /11, с.277¸284/ приведены программы интегрирования дифференциальных уравнений на алгоритмическом языке ФОРТАН. Литература: / 2, с.16¸20,24¸32,51¸54, 88¸92,114¸160/;/10/.
Список литературы
|



 Рис.2 Рис.3
Рис.2 Рис.3 (uу0, Ω∂ в) - М´Н 0
(uу0, Ω∂ в) - М´Н 0 (uу0 + Δu; Ω∂ в 0 + ΔΩ∂ в)–(М´н0 + М´н)
(uу0 + Δu; Ω∂ в 0 + ΔΩ∂ в)–(М´н0 + М´н)
 = tg α = Сu;
= tg α = Сu;  = tg β = СрСu
= tg β = СрСu = Cu Δuу - Ср Сu ΔΩ∂в - М´н
= Cu Δuу - Ср Сu ΔΩ∂в - М´н
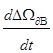 + ΔΩ∂в =
+ ΔΩ∂в =  Δuу -
Δuу -  ΔΜ'н
ΔΜ'н = Т∂в;
= Т∂в;  = Кf
= Кf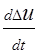 , получаем
, получаем = К∂ Δuу – Кf ΔΜ'н
= К∂ Δuу – Кf ΔΜ'н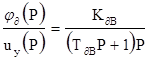


 ΔΩ∂в.
ΔΩ∂в.
 α1
α1  + α2
+ α2  + α3 β(t) = в0 α (t),
+ α3 β(t) = в0 α (t),





