Абсолютные и относительные показатели тенденции
В табл. 3.1 абсолютное изменение уровня не является константой тенденции. Оно со временем возрастает, т.е. уровни ряда изменяются с ускорением. Ускорение - это разность между абсолютным изменением за данный период и абсолютным изменением за предыдущий период равной длительности:
Показатель абсолютного ускорения применяется только в цепном варианте, но не в базисном. Отрицательная величина ускорения говорит о замедлении роста или об ускорении снижения уровней ряда. Как видно из табл. 3.1, ускорение является константой тенденции данного ряда, что свидетельствует о параболической форме этой тенденции.Ее уравнение имеет вид:
где а - средний абсолютный прирост (по всему ряду); b - половина ускорения; ti - номера периодов. По данным табл. 3.1 имеем:
Показатель ускорения абсолютного изменения уровней выражается в единицах измерения уровня, деленных на квадрат длины периода. В нашем случае ускорение составило 4 тыс. т в год за год, или 4 тыс. т-год2. Смысл показателя следующий: объем производства (или добыча угля, руды) имел абсолютный прирост, возрастающий на 4 тыс. т. в год ежегодно. Усвоить рассмотренные показатели поможет следующая аналогия с механическим движением: уровень - это аналог пройденного пути, причем начало его отсчета не в нулевой точке; абсолютный прирост - аналог скорости движения тела, а ускорение абсолютного прироста - аналог ускорения движения. Пройденный телом путь, считая и тот, который уже был пройден до начала отсчета времени в данной задаче, равен:
где s 0 - путь, пройденный до начала отсчета времени; v 0 - начальная скорость; а - ускорение; t - время, прошедшее от начала его отсчета в задаче. Сравнивая с формулой (3.1), видим, что s 0 - аналог свободного члена у 0, v 0 - аналог начального абсолютного изменения a; a /2 - аналог ускорения прироста b. Система показателей должна содержать не только абсолютные, но и относительные статистические показатели. Относительные показатели динамики необходимы для сравнения развития разных объектов, особенно если их абсолютные характеристики различны. Предположим, другое предприятие увеличивало производство аналогичной продукции с тенденцией, выраженной уравнением тренда: у i =20+4t+0,5t2. И абсолютный прирост, и ускорение роста объема продукции во втором предприятии гораздо меньше, чем в первом. Но можно ли ограничиться этими показателями и сделать вывод, что развитие второго предприятия происходит более медленными темпами, чем первого? Меньший уровень еще не есть меньший темп развития, и это покажет относительная характеристика тенденции динамики - темп роста. Темп роста - это отношение сравниваемого уровня (более позднего) к уровню, принятому за базу сравнения (более раннему). Темп роста исчисляется в цепном варианте - к уровню предыдущего года, а в базисном - к одному и тому же, обычно начальному уровню, что иллюстрируется формулой (3.2). Он свидетельствует о том, сколько процентов составляет сравниваемый уровень по отношению к уровню, принятому за базу, или во сколько раз сравниваемый уровень больше уровня, принятого за базу. При этом если уровни снижаются со временем, то сказать, что последующий уровень «больше в 0,33 раза», или составляет 33,3% базового уровня, это, разумеется, означает, что уровень уменьшился в 3 раза. Но будет неверно, если сказать, что «уровень меньше в 0,33 раза». Темп изменения в разах всегда говорит о том, во сколько раз сравниваемый уровень больше. Теперь можно утверждать, что относительная характеристика роста объема продукции на первом предприятии в среднем за год близка к 115% (рост составляет приблизительно 15% в год), и за шесть лет объем продукции увеличился в 2,32 раза, а на втором предприятии, вычислив также шесть уровней параболического тренда, читатель убедится, что в среднем за год объем продукции возрастал примерно на 20%, а за шесть лет он возрос в 3,1 раза. Следовательно, в относительном выражении объем продукции на втором предприятии развивался, возрастал быстрее. Только в сочетании абсолютных и относительных характеристик динамики можно правильно отразить процесс развития совокупности (объекта). Рассмотрим связь абсолютных и относительных показателей динамики. Обозначим темп изменения через k, тогда имеем:
Если сравниваемый уровень выразить через уровень базисного (или предыдущего) периода и абсолютное изменение, получим:
Величина Темп изменения - величина всегда положительная. Если уровень ряда динамики принимает положительные и отрицательные значения, например, финансовый результат от реализации продукции предприятием может быть прибылью (+), а может быть убытком (-), тогда темп изменения и темп прироста применять нельзя. В этом случае такие показатели теряют смысл и не имеют экономической интерпретации. Сохраняют смысл только абсолютные показатели динамики. Рассмотрим соотношения между цепными и базисными показателями на примере данных табл. 3.1: 1) сумма цепных абсолютных изменений равна базисному абсолютному изменению
2) произведение цепных темпов изменения равно базисному темпу изменения
1,12 Неверно, будто сумма цепных темпов прироста равна базисному темпу прироста, %: 12+14,3+15,6+16,2+16,3+16 Значения цепных темпов прироста, рассчитанных каждый к своей базе, различаются не только числом процентов, но и величиной абсолютного изменения, составляющей каждый процент. Следовательно, складывать или вычитать цепные темпы прироста нельзя. Абсолютное значение 1% - ного прироста равно сотой части предыдущего уровня или базисного уровня.
|



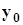 - уровень ряда в начальный (нулевой) период;
- уровень ряда в начальный (нулевой) период;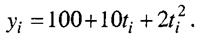



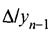 , т.е. отношение абсолютного изменения к уровню предыдущего (или базисного) года, называется относительным приростом (относительным сокращением, относительным изменением, процентным изменением) или темпом прироста. Он равен темпу изменения (роста) минус единица (минус 100%).
, т.е. отношение абсолютного изменения к уровню предыдущего (или базисного) года, называется относительным приростом (относительным сокращением, относительным изменением, процентным изменением) или темпом прироста. Он равен темпу изменения (роста) минус единица (минус 100%).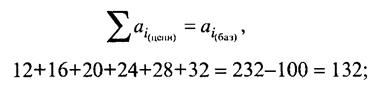

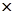 1,143
1,143  132.
132.


