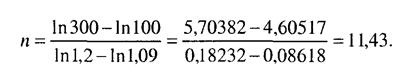Динамика урожайности картофеля в N-й области
По данным табл. 3.2 определим среднегодовые уровни урожайности картофеля по пятилетиям.
Средние уровни принято относить к середине усредняемого отрезка времени, т.е. в нашем примере к средним годам каждого пятилетия. Если, например, с 1-го числа месяца по 18-е число на предприятии работали 45 человек, с 19-го по 27-е - 48 человек, а с 28-го по 31-е число - 54 человека, то среднее списочное число работников за месяц составит:
В моментном ряду смысл среднего уровня заключается в том, что он характеризует уже не состояние объекта в отдельные моменты, а его среднее, обобщенное состояние между начальным и конечным моментами учета. Из этого следует, что уровни, относящиеся к начальному и конечному моментам, играют не ту роль, что уровни, относящиеся к моментам внутри изучаемого отрезка времени. Начальный и конечный уровни находятся на границе изучаемого интервала, они наполовину относятся к предыдущему и последующему интервалам и лишь наполовину к изучаемому. Уровни, относящиеся к моментам внутри усредняемого интервала, целиком относятся только к нему. Отсюда получаем особую форму средней арифметической величины, называемой хронологической средней:
Проблема вычисления среднего уровня моментного ряда при неравных промежутках между моментами является спорной и здесь не рассматривается. Если известны точные даты изменения уровней моментного ряда, то средний уровень определяется как
где ti - время, в течение которого сохранялся уровень. Средний абсолютный прирост (абсолютное изменение) определяется как простая арифметическая средняя из абсолютных изменений за равные промежутки времени (цепных абсолютных изменений) или как частное от деления базисного абсолютного изменения па число усредняемых отрезков времени от базисного до сравниваемого периода:
Например, производство телевизоров в Российской Федерации в 1980 г. составило 4013 тыс. шт., а в 1990 г. - 4717 тыс. шт. Среднегодовой абсолютный прирост производства телевизоров за 10 лет составил:
Для правильной интерпретации показатель среднего абсолютного изменения должен сопровождаться указанием двух единиц времени: 1) времени, за которое он вычислен, к которому относится и которое он характеризует (в нашем примере это десятилетие - 1980-1990 гг.); 2) время, на которое показатель рассчитан, время, входящее в его единицу измерения, - 1 год. Можно рассчитать среднемесячный абсолютный прирост за те же 10 лет - он будет в 12 раз меньше среднегодового прироста. Среднее ускорение абсолютного изменения применяется реже. Для его надежного расчета даже при слабых колебаниях уровней требуется применять методику аналитического выравнивания по параболе II порядка. Не рекомендуется измерять среднее ускорение без абстрагирования от колебаний уровней. Для более грубого, приближенного расчета среднего ускорения можно воспользоваться средними годовыми уровнями, сглаживающими колебания. Например, среднегодовое производство мяса в Российской Федерации составляло:
Абсолютный прирост за второе пятилетие по сравнению с первым составил 0,69 млн. т, за третье по сравнению со вторым 1,59 млн. т. Следовательно, ускорение в третьем пятилетии по сравнению со вторым составило: 1,59 - 0,69 = 0,90 млн. т в год за пять лет, а среднегодовое ускорение прироста равно: 0,90: 5 = = 0,18 млн. т в год за год. Среднее ускорение требует указания трех единиц времени, хотя, как правило, две из них одинаковы: период, на который рассчитан прирост, и время, на которое рассчитано ускорение. Средний темп изменения определяется наиболее точно при аналитическом выравнивании динамического ряда по экспоненте. Если можно пренебречь колеблемостью, то средний темп определяют как геометрическую среднюю из цепных темпов роста за п лет или из общего (базисного) темпа роста за п лет:
Например, стоимость потребительской корзины за год в результате инфляции возросла в шесть раз. Каков средний месячный темп инфляции?
т.е. в среднем за месяц цена увеличивалась на 16% к уровню предыдущего месяца. Средний темп роста так же, как средний прирост, следует сопровождать указанием двух единиц времени: периода, который им характеризуется, и периода, на который рассчитан темп, например, среднегодовой темп за последнее десятилетие; среднемесячный темп за полугодие и т.п. Если исходной информацией служат темпы прироста и нужно вычислить их среднегодовую величину, то предварительно следует все темпы прироста превратить в темпы роста, прибавив 1, или 100%, вычислить их среднюю геометрическую и снова вычесть 1, или 100%. Интересно, что ввиду асимметрии темпа прироста и темпа сокращения при равных их величинах общий темп прироста всегда отрицателен. Так, если за первый год объем производства вырос на 20%), а за второй снизился на 20%> (темпы цепные), то за два года имеем:
Применяя для вычисления среднего темпа среднюю геометрическую, мы опираемся на соблюдение фактического отношения конечного уровня к начальному при замене фактических темпов на средние. В практических задачах может потребоваться вычисление среднего уровня при условии соблюдения отношения суммы уровней за период к уровню, принятому за базу. Например, если общий выпуск продукции за пятилетие должен составить 800% к базисному (среднегодовому за предыдущие 5 лет выпуску), или, что то же самое, среднегодовой уровень должен составить 160% к базовому уровню, каков должен быть среднегодовой темп роста выпуска продукции? В 1974 г. украинские статистики А. и И. Соляники предложили следующую приближенную формулу для среднего темпа роста, удовлетворяющую этому условию:
где т - число суммируемых уровней; У 0 - базисный уровень. Темп роста данного вида называют параболическим (отсюда обозначение
Расчет по этому среднегодовому темпу дает сумму выпуска за 5 лет в 8,069 раза больше базисной, т.е. приближение хорошее. В общем виде проблема параболических темпов исследована саратовским статистиком Л.С. Казинцом [8]. Им составлены таблицы, с помощью которых, зная отношение суммы уровней к базисному уровню и число суммируемых уровней т, можно получить
Для нашего примера таблица Л.С. Казинца дает среднегодовой темп роста 116,1% и сумму выпуска в 8,00016 раза больше базисной. Интересную задачу представляет определение срока, за который ряд с большим средним показателем динамики, но меньшим начальным уровнем догонит другой ряд с большим начальным уровнем, но меньшим показателем динамики. Для абсолютных приростов задача элементарна: имеем один ряд с базисным уровнем
Та же задача может быть решена на основе ускорений. Имеем первый ряд с базисным уровнем
Приравняв правые части уравнений, получим:
Искомый срок п является корнем этого квадратного уравнения. Если, например, имеем:
Второй ряд догонит первый по уровню через 38,4 года; уровнирядов были одинаковы 10,4 года назад. Будущие равные уровнисоставляют 3510, а прошлые были равны 192. Если мы хотим найти срок п, через который уровни рядов сравняются, то эту задачу можно решить на основе темпов изменения. Имеем:
т.е. искомый срок равен частному отделения разности логарифмов уровней рядов в базисном периоде на разность логарифмов темпов изменения, только переставленных при вычитании. Обычно и в числителе, и в знаменателе от большего логарифма вычитается меньший. Например, первый ряд имеет:
Через 11,43 года уровень второго ряда сравняется с первым при сохранении экспоненциальных трендов обоих рядов.
|



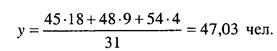
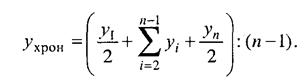
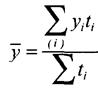

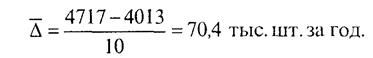

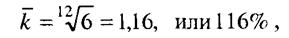
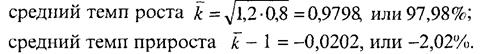
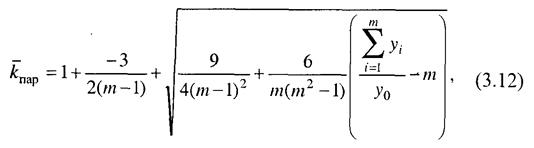
 ), так как он вычисляется по уравнению параболы порядка т. При т. = 5 имеем:
), так как он вычисляется по уравнению параболы порядка т. При т. = 5 имеем:
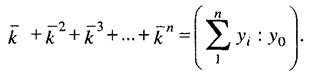
 и средним абсолютным приростом
и средним абсолютным приростом 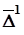 ; второй ряд с показателями соответственно
; второй ряд с показателями соответственно 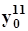 ,
, 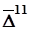 , причем
, причем 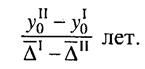
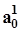 и средним ускорением
и средним ускорением 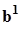 ; второй ряд - с показателями
; второй ряд - с показателями 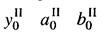 . При каком числе п периодов (лет) после базисного уровни рядов сравняются? Тенденции рядов параболические:
. При каком числе п периодов (лет) после базисного уровни рядов сравняются? Тенденции рядов параболические:
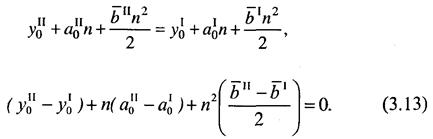
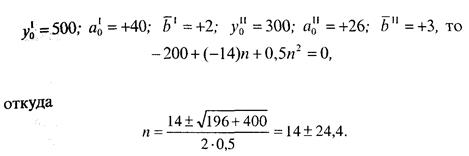
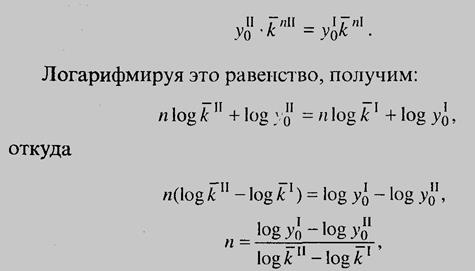
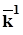 =1,09; второй ряд -
=1,09; второй ряд - 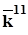 = 1,2, тогда:
= 1,2, тогда: