Решение. Из уравнения Менделеева – Клапейрона
PV= получим плотность:
Откуда, подставив численные значения, имеем:
Пример 3. Найти молярную массу воздуха, считая, что он состоит из одной части кислорода и трех частей азота.
Решение. Воздух, являясь смесью идеальных газов, тоже представляет собой идеальный газ, и к нему можно применить уравние Менделеева–Клапейрона: PV= Для каждого компонента смеси (кислорода и азота) имеем:
где По закону Дальтона Рвозд = Сложив (2) и (3), получим ( или на основании закона Дальтона PV= Сравнив (1) и (5) с учетом того, что mвозд =m
Откуда
Подставив в (6) равенство m
Пример 4. Плотность некоторого газа равна 6·10-2 кг/м3, а среднеквадратичная скорость молекул – 500 м/с. Найти давление, которое газ оказывает на стенку сосуда. Решение. В основном уравнении молекулярно- кинетической теории –
Произведение nm выражает массу молекул, содержащихся в единице объема вещества, и следовательно, равно плотности ρ газа. Таким образом,
Пример 5. 6,5 г водорода, температура которого 270 С, расширяется вдвое при постоянном давлении за счет притока тепла извне. Найти: а) изменение внутренней энергии; б) количество теплоты, сообщенной газу; в) работу расширения. (Мв=2×10-3 кг/моль). Решение. Вычислим значения молярных теплоемкостей водорода, учитывая, что молекулы водорода – двухатомные, а число i степеней свободы равно пяти:
Cр =Cv + R=20,8·103 + 8,31·103 =29,1·103 Дж/моль×К.
|

 RT
RT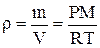 .
. 0,16·10-13 кг/м3.
0,16·10-13 кг/м3. =32×10-3 кг/моль,
=32×10-3 кг/моль,  =28×10-3 кг/моль.
=28×10-3 кг/моль.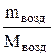 RT. (1)
RT. (1)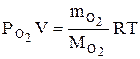 , (2)
, (2)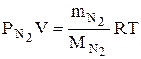 , (3)
, (3)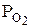 и
и 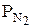 – парциальные давления каждого компонента.
– парциальные давления каждого компонента.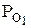 +
+  . (4)
. (4)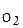 +m
+m 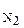 , имеем:
, имеем: . (6)
. (6) =29×10-3 кг/моль.
=29×10-3 кг/моль. .
.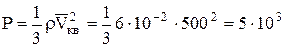 Па.
Па. =20,8·103 Дж/моль×К;
=20,8·103 Дж/моль×К;


