Распределение молекул по скоростям
Молекулы газов движутся с большими скоростями прямолинейно до столкновения. При комнатной температуре скорость молекул воздуха достигает нескольких сотен метров в секунду. Расстояние, которое в среднем пробегают молекулы от одного столкновения до другого, называют средней длиной свободного пробега молекул. У молекул воздуха при комнатной температуре средняя длина свободного пробега порядка 10-7 м. Вследствие хаотичности движения молекулы обладают самыми разными скоростями. Но при данной температуре можно определить скорость, близкой к которой обладает наибольшее число молекул.
Скорость uв, близкой к которой обладает наибольшее число молекул, называется наиболее вероятной скоростью.
Лишь очень малое количество молекул обладает скоростью, близкой к нулю, или близкой к бесконечно большой величине, во много раз превосходящей наиболее вероятную скорость. И, конечно, отсутствуют молекулы, скорость которых равна нулю или бесконечно велика. Зато большинство DN молекул из всех их числа N обладает скоростью, близкой к наиболее вероятной.
 Отношение DN/N представляет собой относительное количество молекул, обладающих теми скоростями, заключенными в интервале скоростей Du. Английский физик Максвелл записал уравнение, позволяющее определить, как зависит относительное число молекул DN/N со скоростями, заключенными в некоторый интервал скоростей Du, от скорости молекул. Графически эта зависимость изображена на рис.. По вертикальной оси здесь отложено относительное количество молекул, скорости которых заключены в интервал Du, а по горизонтальной - любые скорости молекул и от 0 до бесконечно больших величин. Максимальное число молекул обладает скоростями, соответствующими наиболее вероятной скорости uв. График выходит из нуля - это означает, что неподвижных молекул нет. При увеличении скорости кривая графика быстро ниспадает, стремясь к нулю при стремление скорости молекул к бесконечно большим числам. Это свидетельствует о том, что с увеличением скорости количество молекул, обладающих ею, убывает, стремясь к нулю при стремлении скорости к бесконечности.
Отношение DN/N представляет собой относительное количество молекул, обладающих теми скоростями, заключенными в интервале скоростей Du. Английский физик Максвелл записал уравнение, позволяющее определить, как зависит относительное число молекул DN/N со скоростями, заключенными в некоторый интервал скоростей Du, от скорости молекул. Графически эта зависимость изображена на рис.. По вертикальной оси здесь отложено относительное количество молекул, скорости которых заключены в интервал Du, а по горизонтальной - любые скорости молекул и от 0 до бесконечно больших величин. Максимальное число молекул обладает скоростями, соответствующими наиболее вероятной скорости uв. График выходит из нуля - это означает, что неподвижных молекул нет. При увеличении скорости кривая графика быстро ниспадает, стремясь к нулю при стремление скорости молекул к бесконечно большим числам. Это свидетельствует о том, что с увеличением скорости количество молекул, обладающих ею, убывает, стремясь к нулю при стремлении скорости к бесконечности.
С увеличением температуры скорости молекул увеличиваются. Но количество молекул, обладающих скоростью, близкой к наиболее вероятной, уменьшается, так как возрастает разброс в скоростях, возрастает количество молекул, скорости которых существенно отличаются от наиболее вероятной. Число молекул, движущихся с большими скоростями, возрастает, а с меньшими, - уменьшается. Поэтому при повышении температуры максимум кривой распределения молекул по скоростям, получившей название распределения Максвелла, смещается вправо и кривая становится более пологой.
 Из-за огромного количества молекул в любом объеме газа их направления движения вдоль любой оси координат равновероятны, если газ находится в состоянии равновесия, т. е. в нем нет потоков. Это значит, что любому направленному движению одной молекулы соответствует антинаправленное движение другой молекулы с такой же скоростью, т. е. если одна молекула движется, например, вперед, то обязательно найдется другая молекула, которая движется с такой же скоростью назад. Поэтому быстроту движения молекул с учетом их направления нельзя охарактеризовать средней скоростью всех молекул, она всегда будет равна нулю, ведь положительная скорость, сонаправленная с одной из осей координат будет складываться с отрицательной скоростью, антинаправленной этой оси. Если же значения скоростей всех молекул возвести в квадрат, то все минусы исчезнут. Если, затем сложить квадраты скоростей всех молекул, а затем разделить на число молекул N, т. е. определить среднюю, величину квадратов скоростей всех молекул, а затем извлечь квадратный корень из этой величины, то он уже не будет равен нулю и им можно будет охарактеризовать быстроту движения молекул. Корень квадратный из среднего значения квадратов скоростей всех молекул называется их средней квадратичной скоростью
Из-за огромного количества молекул в любом объеме газа их направления движения вдоль любой оси координат равновероятны, если газ находится в состоянии равновесия, т. е. в нем нет потоков. Это значит, что любому направленному движению одной молекулы соответствует антинаправленное движение другой молекулы с такой же скоростью, т. е. если одна молекула движется, например, вперед, то обязательно найдется другая молекула, которая движется с такой же скоростью назад. Поэтому быстроту движения молекул с учетом их направления нельзя охарактеризовать средней скоростью всех молекул, она всегда будет равна нулю, ведь положительная скорость, сонаправленная с одной из осей координат будет складываться с отрицательной скоростью, антинаправленной этой оси. Если же значения скоростей всех молекул возвести в квадрат, то все минусы исчезнут. Если, затем сложить квадраты скоростей всех молекул, а затем разделить на число молекул N, т. е. определить среднюю, величину квадратов скоростей всех молекул, а затем извлечь квадратный корень из этой величины, то он уже не будет равен нулю и им можно будет охарактеризовать быстроту движения молекул. Корень квадратный из среднего значения квадратов скоростей всех молекул называется их средней квадратичной скоростью 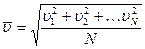 . Из уравнений молекулярной физики следует что
. Из уравнений молекулярной физики следует что  .
.
Опыт Штерна.
Первое экспериментальное определение скорости молекул было сделано в 1920 г. немецким физиком О. Штерном. В нем определялась средняя скорость движения атомов. Схема эксперимента изображена на рис..
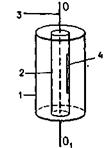
На плоском горизонтальном основании закреплены две коаксиальные цилиндрические поверхности 1 и 2, которые вместе с основанием могут вращаться вокруг вертикальной оси ОО1. Поверхность 1 сплошная, а 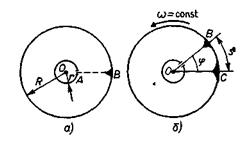 поверхность 2 имеет узкую щель 4, параллельную оси ОО1. Этой осью является платиновая посеребренная проволочка 3, через которую пропускают электрический ток. Вся система находится в камере, из которой откачан воздух (т.е. в вакууме). Проволоку нагревают до высокой температуры. Атомы серебра, испаряясь с ее поверхности, заполняют внутренний цилиндр 2. Узкий пучок этих атомов, прошедший сквозь щель 4 в стенке цилиндра 2, долетает до внутренней поверхности цилиндра 1. Если цилиндры неподвижны, атомы серебра откладываются на этой поверхности в виде узкой полоски, параллельной щели (точка В), (сечение цилиндров горизонтальной плоскостью).
поверхность 2 имеет узкую щель 4, параллельную оси ОО1. Этой осью является платиновая посеребренная проволочка 3, через которую пропускают электрический ток. Вся система находится в камере, из которой откачан воздух (т.е. в вакууме). Проволоку нагревают до высокой температуры. Атомы серебра, испаряясь с ее поверхности, заполняют внутренний цилиндр 2. Узкий пучок этих атомов, прошедший сквозь щель 4 в стенке цилиндра 2, долетает до внутренней поверхности цилиндра 1. Если цилиндры неподвижны, атомы серебра откладываются на этой поверхности в виде узкой полоски, параллельной щели (точка В), (сечение цилиндров горизонтальной плоскостью).
Когда цилиндры приводят во вращение с постоянной угловой скоростью w вокруг оси ОО1 за время t, в течение которого атомы летят от щели до поверхности внешнего цилиндра (т. е. проходят расстояние АВ, равное разности  радиусов этих цилиндров), цилиндры поворачиваются на угол j, и атомы осаждаются в виде полоски в другом месте (точка С, рис. б). Расстояние между местами осаждения атомов в первом и во втором случаях равно s.
радиусов этих цилиндров), цилиндры поворачиваются на угол j, и атомы осаждаются в виде полоски в другом месте (точка С, рис. б). Расстояние между местами осаждения атомов в первом и во втором случаях равно s.
Обозначим 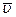 среднюю скорость движения атомов, а v = wR - линейную скорость наружного цилиндра. Тогда
среднюю скорость движения атомов, а v = wR - линейную скорость наружного цилиндра. Тогда  . Зная параметры установки и измерив экспериментально s, по можно определить среднюю скорость движения атомов. В опыте Штерна было установлено, что средняя скорость атомов серебра равна 650 м/с.
. Зная параметры установки и измерив экспериментально s, по можно определить среднюю скорость движения атомов. В опыте Штерна было установлено, что средняя скорость атомов серебра равна 650 м/с.

 Отношение DN/N представляет собой относительное количество молекул, обладающих теми скоростями, заключенными в интервале скоростей Du. Английский физик Максвелл записал уравнение, позволяющее определить, как зависит относительное число молекул DN/N со скоростями, заключенными в некоторый интервал скоростей Du, от скорости молекул. Графически эта зависимость изображена на рис.. По вертикальной оси здесь отложено относительное количество молекул, скорости которых заключены в интервал Du, а по горизонтальной - любые скорости молекул и от 0 до бесконечно больших величин. Максимальное число молекул обладает скоростями, соответствующими наиболее вероятной скорости uв. График выходит из нуля - это означает, что неподвижных молекул нет. При увеличении скорости кривая графика быстро ниспадает, стремясь к нулю при стремление скорости молекул к бесконечно большим числам. Это свидетельствует о том, что с увеличением скорости количество молекул, обладающих ею, убывает, стремясь к нулю при стремлении скорости к бесконечности.
Отношение DN/N представляет собой относительное количество молекул, обладающих теми скоростями, заключенными в интервале скоростей Du. Английский физик Максвелл записал уравнение, позволяющее определить, как зависит относительное число молекул DN/N со скоростями, заключенными в некоторый интервал скоростей Du, от скорости молекул. Графически эта зависимость изображена на рис.. По вертикальной оси здесь отложено относительное количество молекул, скорости которых заключены в интервал Du, а по горизонтальной - любые скорости молекул и от 0 до бесконечно больших величин. Максимальное число молекул обладает скоростями, соответствующими наиболее вероятной скорости uв. График выходит из нуля - это означает, что неподвижных молекул нет. При увеличении скорости кривая графика быстро ниспадает, стремясь к нулю при стремление скорости молекул к бесконечно большим числам. Это свидетельствует о том, что с увеличением скорости количество молекул, обладающих ею, убывает, стремясь к нулю при стремлении скорости к бесконечности. Из-за огромного количества молекул в любом объеме газа их направления движения вдоль любой оси координат равновероятны, если газ находится в состоянии равновесия, т. е. в нем нет потоков. Это значит, что любому направленному движению одной молекулы соответствует антинаправленное движение другой молекулы с такой же скоростью, т. е. если одна молекула движется, например, вперед, то обязательно найдется другая молекула, которая движется с такой же скоростью назад. Поэтому быстроту движения молекул с учетом их направления нельзя охарактеризовать средней скоростью всех молекул, она всегда будет равна нулю, ведь положительная скорость, сонаправленная с одной из осей координат будет складываться с отрицательной скоростью, антинаправленной этой оси. Если же значения скоростей всех молекул возвести в квадрат, то все минусы исчезнут. Если, затем сложить квадраты скоростей всех молекул, а затем разделить на число молекул N, т. е. определить среднюю, величину квадратов скоростей всех молекул, а затем извлечь квадратный корень из этой величины, то он уже не будет равен нулю и им можно будет охарактеризовать быстроту движения молекул. Корень квадратный из среднего значения квадратов скоростей всех молекул называется их средней квадратичной скоростью
Из-за огромного количества молекул в любом объеме газа их направления движения вдоль любой оси координат равновероятны, если газ находится в состоянии равновесия, т. е. в нем нет потоков. Это значит, что любому направленному движению одной молекулы соответствует антинаправленное движение другой молекулы с такой же скоростью, т. е. если одна молекула движется, например, вперед, то обязательно найдется другая молекула, которая движется с такой же скоростью назад. Поэтому быстроту движения молекул с учетом их направления нельзя охарактеризовать средней скоростью всех молекул, она всегда будет равна нулю, ведь положительная скорость, сонаправленная с одной из осей координат будет складываться с отрицательной скоростью, антинаправленной этой оси. Если же значения скоростей всех молекул возвести в квадрат, то все минусы исчезнут. Если, затем сложить квадраты скоростей всех молекул, а затем разделить на число молекул N, т. е. определить среднюю, величину квадратов скоростей всех молекул, а затем извлечь квадратный корень из этой величины, то он уже не будет равен нулю и им можно будет охарактеризовать быстроту движения молекул. Корень квадратный из среднего значения квадратов скоростей всех молекул называется их средней квадратичной скоростью 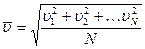 . Из уравнений молекулярной физики следует что
. Из уравнений молекулярной физики следует что  .
. поверхность 2 имеет узкую щель 4, параллельную оси ОО1. Этой осью является платиновая посеребренная проволочка 3, через которую пропускают электрический ток. Вся система находится в камере, из которой откачан воздух (т.е. в вакууме). Проволоку нагревают до высокой температуры. Атомы серебра, испаряясь с ее поверхности, заполняют внутренний цилиндр 2. Узкий пучок этих атомов, прошедший сквозь щель 4 в стенке цилиндра 2, долетает до внутренней поверхности цилиндра 1. Если цилиндры неподвижны, атомы серебра откладываются на этой поверхности в виде узкой полоски, параллельной щели (точка В), (сечение цилиндров горизонтальной плоскостью).
поверхность 2 имеет узкую щель 4, параллельную оси ОО1. Этой осью является платиновая посеребренная проволочка 3, через которую пропускают электрический ток. Вся система находится в камере, из которой откачан воздух (т.е. в вакууме). Проволоку нагревают до высокой температуры. Атомы серебра, испаряясь с ее поверхности, заполняют внутренний цилиндр 2. Узкий пучок этих атомов, прошедший сквозь щель 4 в стенке цилиндра 2, долетает до внутренней поверхности цилиндра 1. Если цилиндры неподвижны, атомы серебра откладываются на этой поверхности в виде узкой полоски, параллельной щели (точка В), (сечение цилиндров горизонтальной плоскостью). радиусов этих цилиндров), цилиндры поворачиваются на угол j, и атомы осаждаются в виде полоски в другом месте (точка С, рис. б). Расстояние между местами осаждения атомов в первом и во втором случаях равно s.
радиусов этих цилиндров), цилиндры поворачиваются на угол j, и атомы осаждаются в виде полоски в другом месте (точка С, рис. б). Расстояние между местами осаждения атомов в первом и во втором случаях равно s.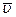 среднюю скорость движения атомов, а v = wR - линейную скорость наружного цилиндра. Тогда
среднюю скорость движения атомов, а v = wR - линейную скорость наружного цилиндра. Тогда  . Зная параметры установки и измерив экспериментально s, по можно определить среднюю скорость движения атомов. В опыте Штерна было установлено, что средняя скорость атомов серебра равна 650 м/с.
. Зная параметры установки и измерив экспериментально s, по можно определить среднюю скорость движения атомов. В опыте Штерна было установлено, что средняя скорость атомов серебра равна 650 м/с.


