Основные типы задач и методы их решения. 1. Нахождение характеристик тепловых и холодильных машин, определение их эффективности.
Классификация. 1. Нахождение характеристик тепловых и холодильных машин, определение их эффективности. Метод решения. 1) Представление тепловой или холодильной машины в виде соответствующего обратимого цикла на диаграмме рV. Определение вида машин; 2). Проведение энергетических расчетов на основе уравнения состояния для рабочего тела и уравнений процессов для участка цикла. 2. Подсчет изменений энтропии при переходе из одного состояния в другое. Метод решения. Использование формулы Следует учитывать, что независимо от процесса, который перевел систему из одного состояния в другое, подсчет изменения энтропии целесообразно проводить по тому пути, который связан с наибольшей простотой расчета. Примеры. Задача 1. Определить КПД цикла, состоящего из двух изобар и двух изохор, если в пределах цикла давление изменяется в n=2 раза, а объем в n=4 раза. Рабочим веществом является один моль идеального газа с показателем адиабаты g. Решение
Интеграл по замкнутому контуру может быть заменен суммой интегралов, либо алгебраической суммой работ на каждом участке. Эта работа положительна, так как
Найдем теплоту, которую получает или отдает рабочее тело на каждом этапе цикла. Этапы 1-2 и 3-4 представляют собой изобарические процессы, поэтому
Для этапов 2-3 и 4-1, являющихся изохорическими, найдем
Температуры нам не заданы, но их легко определить, используя уравнения состояния для идеального газа. Действительно, так как
Таким образом, для данного случая КПД равен
Окончательно, с учетом того, что
Задача 2. Тепловую машину, работающую по циклу Карно с К.П.Д. = 40%, начинают использовать при тех же условиях как холодильную машину. Найти величину холодильного коэффициента и количество теплоты, которое эта машина может перенести за один цикл от холодильника к нагревателю, если к ней за каждый цикл подводится механическая работа, равная 200 Дж. Решение.
где При этом
Записав уравнения адиабат для процессов 1-2 и 3-4
С учетом того, что T1=T4 и T2=T3 получим
Тогда
Работа внешних сил за цикл
Таким образом, С другой стороны, при осуществлении прямого цикла Карно
где
Подстановка числовых значений дает:
Задача 3. Найти изменение энтропии при переходе 6 г водорода от объема в 20 л под давлением 1,5×105 Па к объему в 60 л под давлением в 1×105 Па. Решение. По первому закону термодинамики
Применяя уравнение Менделеева-Клапейрона
получим
Из уравнения Менделеева-Клайперона
С учетом последнего соотношения
где теплоемкости при постоянном объеме и постоянном давлении для водорода соответственно равны
Подставив числовые значения, получим
Задача 4. Кислород, масса которого 0,2 кг нагревают от температуры Т1 = 300 К до Т2 = 400 К. Найти изменение энтропии, если известно, что начальное и конечное давление одинаковы. Решение.
Найти изменение энтропии можно по формуле
Легко проверить, что результат не изменится и при переходе 1-3-2
где Для изотермического процесса
Учитывая, что Т3 = Т1, V3 = V2, а также получим Для кислорода i = 5, и
|

 .
. Представим данный цикл на рV – диаграмме (рис.2). При данной последовательности состояний (обход контура происходит по часовой стрелке) система работает как тепловая машина с КПД
Представим данный цикл на рV – диаграмме (рис.2). При данной последовательности состояний (обход контура происходит по часовой стрелке) система работает как тепловая машина с КПД 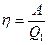 . Полная работа А, совершенная рабочим телом, за цикл определяется выражением
. Полная работа А, совершенная рабочим телом, за цикл определяется выражением
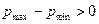 ,
,  .
.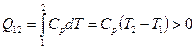 ,
,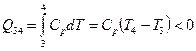 .
. ,
,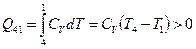 .
.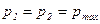 , имеем
, имеем  или
или 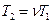 и аналогично
и аналогично  . С другой стороны, для
. С другой стороны, для 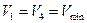 имеем
имеем  или
или  и аналогично
и аналогично  . Общее количество теплоты, получаемое от нагревателей, равно
. Общее количество теплоты, получаемое от нагревателей, равно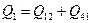 .
.
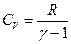 получим
получим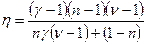 .
. В данном случае холодильная машина будет работать по обратному циклу Карно (рис.3). Эффективность такой машины можно охарактеризовать отношением отнятой у холодильника теплоты
В данном случае холодильная машина будет работать по обратному циклу Карно (рис.3). Эффективность такой машины можно охарактеризовать отношением отнятой у холодильника теплоты 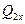 к совершаемой для этого работе внешних сил А*:
к совершаемой для этого работе внешних сил А*: 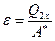 . Эту величину принято называть холодильным коэффициентом. Полная работа за цикл, согласно первому началу термодинамики, примененному к циклическому процессу, равна полному количеству теплоты, получаемой и отдаваемой за цикл:
. Эту величину принято называть холодильным коэффициентом. Полная работа за цикл, согласно первому началу термодинамики, примененному к циклическому процессу, равна полному количеству теплоты, получаемой и отдаваемой за цикл: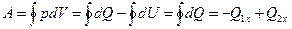
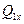 - количество тепла, переданного окружающей среде.
- количество тепла, переданного окружающей среде.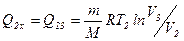 ,
,  .
. ,
, .
. .
. .
.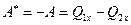
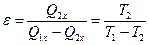 .
. ,
, - количество тепла, полученного от нагревателя,
- количество тепла, полученного от нагревателя, 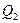 - количество тепла, переданного холодильнику. Поскольку машина обратима, она забирает от холодильника столько же теплоты, сколько передает ему при прямом цикле. Отсюда
- количество тепла, переданного холодильнику. Поскольку машина обратима, она забирает от холодильника столько же теплоты, сколько передает ему при прямом цикле. Отсюда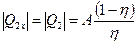 ,
, .
. 300 Дж, e = 1,5
300 Дж, e = 1,5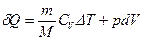 .
.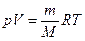 ,
,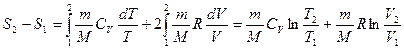 .
. .
. .
. ,
,  .
.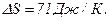
 Изменение энтропии системы при переходе из одного состояния в другое определяется только параметрами этих состояний и не зависит от характера процесса.
Изменение энтропии системы при переходе из одного состояния в другое определяется только параметрами этих состояний и не зависит от характера процесса.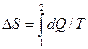 , рассматривая произвольный обратимый процесс, например, изобарический переход 1-2 или изотермическое расширение с последующим изохорным нагревом 1-3-2 (рис.4). Найдем изменение энтропии процесса 1-2.
, рассматривая произвольный обратимый процесс, например, изобарический переход 1-2 или изотермическое расширение с последующим изохорным нагревом 1-3-2 (рис.4). Найдем изменение энтропии процесса 1-2. ,
, 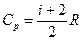
 .
.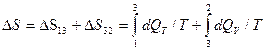 ,
,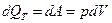 ,
, 
 ,
, ,
,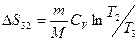 .
.

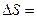 52 Дж/К.
52 Дж/К.


