Процессы в газах
Уравнение процесса задается функциональной связью двух макроскопических параметров, описывающих систему. На соответствующей координатной плоскости (PV, TV или PT) уравнение процесса наглядно представляется в виде графика (кривой процесса). Уравнение определенного процесса может быть получено с помощью первого начала термодинамики, а также информации о процессе и системе: U(T,V), p(T,V), Сα(Т). Важный класс процессов составляют политропические процессы. Политропическим называется процесс, проходящий при постоянной теплоемкости С. Кривая, изображающая политропический процесс, называется политропой.
Задачи 1.1. Найти уравнение политропы для идеального газа, теплоемкость Cv которого не зависит от температуры. Рассмотреть частные случаи: а) С= Cv, б) С= Cp, в) С=0, г) С=∞;; построить соответствующие графики процессов.
1.3. При каких значениях показателя политропы n идеальный газ при сжатии нагревается, а при каких охлаждается? Нагревается или охлаждается идеальный газ и какова его молярная теплоемкость, если он расширяется по закону: а) pV²=const; б) p²V=const?
1.4. Найти уравнение процесса для идеального газа, при котором теплоемкость газа меняется с температурой по закону С= αТ, где α – постоянная. 1.5 Состояние идеального газа изменяется по политропе а) p=kV, б) pVn=const.. Найти работу, совершаемую молем газа при повышении его температуры от T1 до T2. 1.6. Процесс перехода моля идеального газа из состояния А с параметрами p1,V1 в состояние В с параметрами p2, V2 представлен графически в переменных pV прямой линией АВ. Молярная теплоемкость Cv в данных условиях не зависит от температуры (рис.3). Найти уравнение процесса АВ, определить молярную теплоемкость в этом процессе. 1.7. Записать условиеперехода процесса АВ (рис.3) в политропический. Вычислить молярную теплоемкость для полученного политропического процесса. Ответы 1.1. TVn-1=const, pVn=const, где 1.2. а) V=const, б) p=const, в) pVγ=const, г) pV=const. 1.3. Нагревается при n>1, охлаждается при n<1 а) охлаждается, С=Сv-R, б) нагревается, С=Сp+R. 1.4. 1.5. а) 1.6.
|


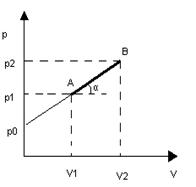 1.2. Выразить С политропического процесса через постоянные R, γ, n. Изобразить политропы для
1.2. Выразить С политропического процесса через постоянные R, γ, n. Изобразить политропы для 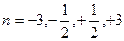 . Рассчитать соответствующие теплоемкости.
. Рассчитать соответствующие теплоемкости.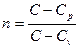 ;
;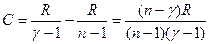 ;
;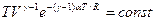 ,где
,где 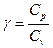 ;
;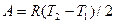 ;б)
;б) 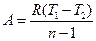 ;
;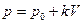 ;
; 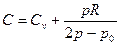 ; где k=tgα, p0- const.
; где k=tgα, p0- const.


