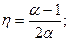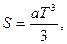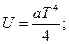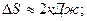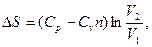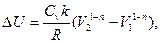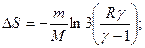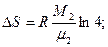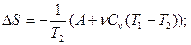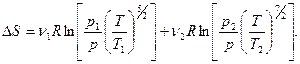Семинар 3. Второе начало термодинамики. Энтропия
Второе начало термодинамики имеет особый статус не только фундаментального закона физики, но и универсального принципа естествознания в целом. Второе начало дает информацию о направлении процессов, которые могут происходить в действительности. Оно, совместно с первым началом, позволяет установить множество точных количественных соотношений между различными макроскопическими параметрами тел в состоянии термодинамического равновесия. Это оказывается возможным благодаря определению такой величины как энтропия через теплоту. Энтропия (греч. – поворот, превращение) служит мерой преобразования или эволюции системы. Существует несколько десятков различных формулировок второго начала. В большинстве из них термин «энтропия» не используется (см. формулировки Кельвина, Клаузиуса и Оствальда).
Такие процессы невозможны. Они запрещены вторым началом.
Часть первая. Каждая термодинамическая система обладает функцией состояния, называемой энтропией. Энтропия вычисляется следующим образом. Система переводится из произвольно выбранного начального состояния в соответствующее конечное состояние через последовательность состояний равновесия. Вычисляются все подводимые при этом к системе порции тепла
Часть вторая. При реальных (не идеальных) процессах энтропия замкнутой системы возрастает.
Содержание второй части формулировки А.Зоммерфельда в большинстве учебников рассматривается как самодостаточная формулировка второго начала, или как закон возрастания энтропии:
Энтропия не убывает только в процессах изолированной системы, в неизолированной системе энтропия может и возрастать, и убывать, и оставаться неизменной. Рост энтропии в изолированной системе означает приближение системы к состоянию термодинамического равновесия; в этом состоянии S – максимальна, а dS=0. Расчет изменения энтропии в различных процессах изучаемых систем зачастую является актуальной внутренней подзадачей разнообразных задач термодинамики, химии биологии, лингвистики. В частности, изменение энтропии служит мерой изменения качества энергии. Важнейшим условием для тепловых машин, работающих по произвольному циклу, является условие их максимально допустимой эффективности:
Большинство процессов, происходящих в природе, необратимы, например: диффузия, расширение, растворение. Для таких процессов вычисление энтропии основывается на том, что S – функция состояния. Если система перешла из одного состояния в другое необратимым образом, то можно мысленно заменить необратимый процесс обратимым, причем начальное и конечное состояния этого процесса должны быть равновесны, рассчитанное в этом случае изменение энтропии будет равно изменению энтропии при реальном необратимом процессе.
Задачи
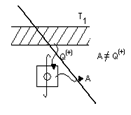
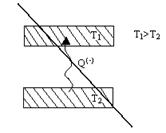
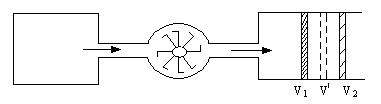
3.3. Найти приращение энтропии алюминиевого бруска массы m=3.0кг при нагревании его от Т1=300˚К до Т2=600˚К, если в этом интервале температур удельная теплоемкость алюминия с=а+bТ, где а=0,77Дж/гК, b=0.46мДж/гК2. 3.4. Вычислить изменения внутренней энергии и энтропии одного моля идеального газа при расширении по политропе pVn=const от объема V1 до объема V2. рассмотреть частные случаи изотермического и адиабатического процессов. 3.5. Гелий массы m=1,7г адиабатически расширили в n=3 раза и затем изобарически сжали до первоначального объема. Найти приращение энтропии газа в этом процессе. 3.6. В двух сосудах одного и того же объема находятся различные идеальные газы. Масса газа в первом сосуде М1, во втором М2, давления газов и их температуры одинаковы. Сосуды соединили друг с другом и начался процесс диффузии. Определить суммарное изменение ∆S энтропии рассматриваемой системы, если относительная молекулярная масса первого газа μ1, а второго μ2. 3.7. Идеальный одноатомный газ в количестве υ=10 молей, находящийся при температуре Т1=300˚К, расширяется без подвода и отдачи тепла в пустой сосуд через турбину, необратимым образом совершая работу (рис.16) После установления равновесия температура газа понижается до Т=200˚К.
После этого газ квазистатически сжимается: сначала изотермически, а затем адиабатически, возвращаясь в первоначальное состояние. При этом сжатии затрачивается работа А=15кДж. Найти изменение энтропии газа при расширении. 3.8. Вычислить изменение энтропии при смешении одноатомного идеального газа массы m1, имеющего начальную температуру Т1 и давление p1, и двухатомного газа массы m2, имеющего начальные температуру Т2 и давление p2. Молярные массы смешиваемых газов М1 и М2.
Ответы 3.1. 3.2. 3.3. 3.4. где k=const; 3.5. 3.6. 3.7. 3.8.
|

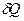 , делятся каждая на соответствующую ей абсолютную температуру Т и все полученные таким образом значения суммируются.
, делятся каждая на соответствующую ей абсолютную температуру Т и все полученные таким образом значения суммируются.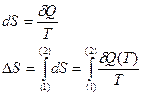 (13)
(13)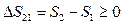 (14)
(14)
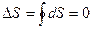 (за цикл) (15)
(за цикл) (15)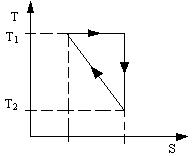
 3.1. Произвольное рабочее вещество совершает цикл, в пределах которого абсолютная температура изменяется в α раз. Цикл имеет вид изображенный на рис.15: T – температура, S – энтропия. Найти КПД цикла.
3.1. Произвольное рабочее вещество совершает цикл, в пределах которого абсолютная температура изменяется в α раз. Цикл имеет вид изображенный на рис.15: T – температура, S – энтропия. Найти КПД цикла.