Семинар 4. Реальные газы
Существует множество уравнений реальных газов, адекватно описывающих их свойства, включая превращение в жидкость. Это уравнения Ван-дер-Ваальса, Дитеричи (16), Бертло (17), Клаузиуса (18). Наиболее популярные в современной научной практике уравнения Редлиха-Квонга, Пенга-Робинсона, Камерлинг-Оннеса, или вириальное уравнение (19). Уравнение Ван-дер-Ваальса имеет наиболее простую и физически ясную структуру, позволяющую сравнительно легко получать решение в аналитической форме. По этим причинам на семинаре мы ограничимся рассмотрением именно этого уравнения. Исторически это было первое уравнение состояния неидеального газа, поэтому наш выбор отражает также и почтение к его автору. Взаимодействие молекул на далеких и близких расстояниях удобно характеризовать потенциальной энергией взаимодействия
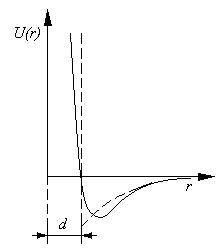
Функция имеет минимум, в котором силы притяжения уравновешиваются силами отталкивания. Аналитический вид функции
В теории Ван-дер-Ваальса используется упрощенная модель межмолекулярного взаимодействия, часть кривой
где
Такая температура и соответствующая ей изотерма называются критическими. Критическая изотерма всюду монотонно опускается вниз, за исключением одной точки – критической.
точке давление pk, объем Vk и температура Tk также называются критическими.
|

 Уравнение состояния газа Клапейрона-Менделеева имеет ограниченную область применимости, поскольку не учитывает межмолекулярные взаимодействия. В реальных газах есть дальнодействующие силы притяжения и короткодействующие силы отталкивания. Взаимодействие в газах приводит к количественным и качественным отклонениям от поведения, предсказываемого уравнением Клапейрона-Менделеева.
Уравнение состояния газа Клапейрона-Менделеева имеет ограниченную область применимости, поскольку не учитывает межмолекулярные взаимодействия. В реальных газах есть дальнодействующие силы притяжения и короткодействующие силы отталкивания. Взаимодействие в газах приводит к количественным и качественным отклонениям от поведения, предсказываемого уравнением Клапейрона-Менделеева.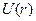 , функцией расстояния r между центрами молекул (рис.17).
, функцией расстояния r между центрами молекул (рис.17).
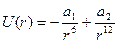 - потенциал Леннарда-Джонса (20)
- потенциал Леннарда-Джонса (20)
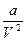 – поправка на давление, т.е. дополнительное «внутреннее» давление за счет взаимного притяжения; b – поправка на объем молекул, учитывающая силы отталкивания.
– поправка на давление, т.е. дополнительное «внутреннее» давление за счет взаимного притяжения; b – поправка на объем молекул, учитывающая силы отталкивания.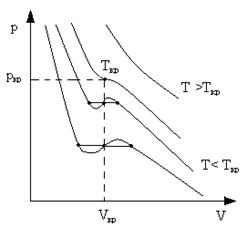 Наиболее содержательные результаты получаются из уравнения Ван-дер-Ваальса путем анализа его изотерм. Если в уравнении (19) принять Т = const, то изотерма этого уравнения в плоскости p, V пересекается прямой линией p = const либо в одной точке, либо в трех точках (рис.18). При некоторой промежуточной температуре Ткр три корня V1, V2, V3 становятся равными.
Наиболее содержательные результаты получаются из уравнения Ван-дер-Ваальса путем анализа его изотерм. Если в уравнении (19) принять Т = const, то изотерма этого уравнения в плоскости p, V пересекается прямой линией p = const либо в одной точке, либо в трех точках (рис.18). При некоторой промежуточной температуре Ткр три корня V1, V2, V3 становятся равными.


