РИСК И ВОЗНАГРАЖДЕНИЕ

 

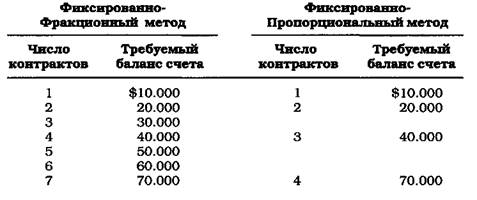
Правильное управление капиталом в первую очередь затрагивает два аспекта торговли: риск и вознаграждение. Трейдер не может решить вопрос о риске, не уделив должного внимания вопросу о вознаг­раждении, и при этом ожидать какого-либо дохода от управления ка­питалом. Это - одна из основных проблем Фиксированно-Фракционно­го метода. Любая вариация этого метода либо предполагает рост при­были без учета общих рисков (как, например, оптимальная фракция), либо занимается исключительно управлением рисками (как, напри­мер, риск в размере менее 3% по каждой сделке), все это невольно при­водит к тому, что прибыль не может подняться до необходимого уров­ня, подобно птице с одним крылом. Делались попытки совместить уп­равление риском и вознаграждением, используя нечто среднее между вариантом "ставка риска, не превышающая 3%", и оптимальной фрак­цией. Однако эффективность такого метода не подтвердилась. Поэто­му в рамках Фиксированно-Фракционного метода задачи, связанные с риском и вознаграждением, адекватно решить не получается.

Цель разработки нового метода управления капиталом состояла в том, чтобы получить возможность учитывать как риски, так и вознаг­раждение в управлении капиталом вообще. Как уже указывалось вы­ше, в ситуации с положительным исходом может применяться только один тип управления капиталом, а именно: "Анти-Мартингейл". Это означает, что по мере роста собственного капитала размер инвестиций или же объем сделки должен также иметь тенденцию к увеличению. По мере снижения оборотных средств величина инвестиций и размер тор­говой сделки также должны уменьшаться. Этот тип методов противо­положен "Мартингейлу", в котором по мере снижения собственных средств объем торговли увеличивается. Поэтому должен использовать­ся тот же тип управления капиталом, к которому принадлежит и Фиксированно-Фракционный метод. Опираясь на эти соображения, я со­ставил список доводов "за" и "против" использования метода "Анти-Мартингейл". Этот список выглядит следующим образом:

"За";:

1. Геометрический рост может достигаться с помощью более вы­соких процентных долей.

2. Риск может сдерживаться менее значительными процентными долями.

"Против";:

1. Использование более высоких процентных долей подвергает счет катастрофическому риску.

2. Использование все меньших процентных долей требует слишком много времени, чтобы реализовать задуманные стратегии, поэтому этот путь становится неэффективным.

3. Использование промежуточных процентных долей не позволя­ет установить правильную пропорцию между имеющимися по­тенциалами вознаграждения и риска.

После некоторого размышления над доводами "за" и "против" я ре­шил, что корень проблемы заключается в том, что по мере расширения торговли требуются разные объемы прибыли. Согласно Фиксирован­но-Фракционному методу, вначале необходимо обеспечить большие прибыли, а по мере роста капитала норма прибыли уменьшается. Это, по-моему, неразумно. Я считаю, что все должно быть наоборот. Пра­вильный метод управления капиталом предполагает меньшие прибы­ли в начале торговли (и, как следствие, более стойкие результаты) и большие прибыли по мере роста капитала (что решает проблему риска).

Сначала я провел испытание различных способов увеличения суммы капитала, необходимой для приобретения новых контрактов, и эти способы показались мне не вполне надежными. Тогда мне стало яс­но, что необходимо выявить соотношение между числом торгуемых контрактов и суммой прибыли, которая необходима для того, чтобы увеличить число контрактов на одну единицу. Это должна быть посто­янная величина. Допустим, если управление капиталом предполагает 10.000 долларов прибыли для перехода от торговли одним контрактом к торговле двумя контрактами, то для увеличения торгуемых контрак­тов до трех нужно планировать 20.000 долларов прибыли. Именно так должна действовать постоянная пропорция между контрактами и тре­буемым размером прибыли, иными словами, фиксированная пропор­ция, которую я положил в основу нового метода управления капита­лом.

Единственная переменная величина в методе фиксированных пропорций называется дельта. Эта переменная просто обеспечивает математическую формулировку метода, а также определяет, насколько агрессивно или консервативно следует вести управление. Чем меньше значение переменной, тем более агрессивным должно быть управле­ние ресурсами. Чем больше величина переменной, тем более консерва­тивно управление. Кривая Гаусса в Фиксированно-Пропорциональном методе не используется.

Следующее сравнение Фиксированно-Фракционного и Фиксиро­ванно-Пропорционального метода показывает, где находятся уровни увеличения и как они соотносятся друг с другом:

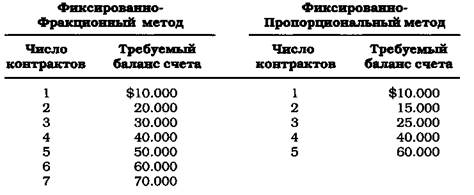
Согласно методу фиксированной пропорции, по мере роста числа контрактов сумма, необходимая для приобретения очередного количе­ства контрактов, увеличивается пропорционально. В результате риск оказывается значительно ниже тех уровней, которые характерны для Фиксированно-Фракционного метода. Кроме того, эта шкала показы­вает, что геометрический рост прибыли происходит значительно быс­трее, чем может позволить Фиксированно-Фракционный метод. Дей­ствительно, если исключить эффект асимметричного действия рыча­га, то при использовании Фиксированно-Фракционного метода потре­буется 19.375 долларов из расчета на один контракт, чтобы достичь ве­личины счета в размере 70.000 долларов. При использовании Фикси­рованно-Пропорционального метода, предполагающего торговлю од­ним контрактом на 10.000 долларов прибыли, потребуется 40.000 дол­ларов, чтобы достичь уровня в 70.000 долларов. Это в два раза больше, чем в случае с Фиксированно-Фракционным методом.

Величина соотношения меньше, поскольку метод фиксированной пропорции значительно снижает риск. Одна из проблем Фиксирован­но-Фракционного метода состоит в том, что он требует слишком много времени на прирост капитала до суммы, которой можно управлять. Метод фиксированной пропорции уменьшает риск в масштабах всего процесса торговли, поэтому управление капиталом включается уже на начальных этапах. Сравнение методов фиксированной пропорции и фиксированной фракции при меньшей величине дельты (или по-иному - фиксированной пропорции):

В этом случае Фиксированно-Фракционный метод работает по схеме "один контракт на каждые 10.000 долларов на счете", а дельта метода фиксированной пропорции равна 5.000 долларов. В результате для достижения уровня в 60.000 долларов потребовалось всего 20.000 долларов вместо 40.000 долларов для достижения 70.000 долларов. Да­лее, еще 5.000 долларов прибыли позволят увеличить размер счета до 85.000 долларов. Как видим, геометрическое увеличение счета в этом случае идет очень интенсивно.

Формула для расчета уровней возможного увеличения числа кон­трактов (опционов или акций) выглядит следующим образом:

Капитал

предыдущего + (число контрактов х дельта) = следующий уровень

Начальный баланс =$10.000 (капитал первоначального уровня)

Число контрактов = 1

Дельта = $5.000

$10.000 + (1 х $5.000) = $15.000 чтобы увеличить число контрактов на 1

Если баланс счета превысит 15.000 долларов, то $15.000 станет исходным требуемым уровнем в уравнении:

$15.000 + (2 х $5.000) = $25.000 $25.000 + (3 х $5.000) = $40.000 $40.000 + (4 х $5.000) = $60.000 $60.000 + (5 х $5.000) = $85.000

Дельта лежит в основе изменений. Это - единственная варьируе­мая константа в уравнении, которую пользователь свободно изменяет в соответствии со своим методом и/или стилем торговли. Также дельта может изменять динамику исхода. Общее правило такое: чем меньше дельта, тем более агрессивным может быть управление капиталом, а чем дельта больше, тем более консервативным становится метод.

В основу Фиксированно - Пропорциональной торговли заложена взаимосвязь требуемой суммы и числа контрактов, торгуемых для до­стижения этой суммы. Это соотношение 1:1. Помножьте число кон­трактов и сумму, которая необходима для увеличения числа контрак­тов на одну единицу, на одно и то же число. Если соотношение равно 1:5.000 долларов, то для увеличения числа торгуемых контрактов с 10 до 11 вам потребуется получить прибыль в размере 50.000 долларов:

1x10= 10 $5.000x10 = $50.000

Это число не совпадает с требуемым балансом счета. Эта величи­на является суммой дополнительной прибыли, необходимой для того, чтобы перейти на следующий уровень увеличения.

Благодаря этому соотношению в системе возникают другие соот­ношения, которые позволяют нам извлекать дополнительную при­быль. Во-первых, используя это соотношение, мы можем оценить ре­зультат работы любой торговой системы или стратегии просто с помо­щью статистики. Если после 100 торговых сделок на рынке бондов трейдер получает 50.000 прибыли, то средняя сделка дает 500 долла­ров ($50.000 / 100 = $500). Сумма средств, необходимая для наращива­ния числа контрактов, строго пропорционально зависит от числа тор­гуемых контрактов. Значит, средняя сделка дает нам 500 долларов при дельте в 5.000 долларов и мы имеем возможность увеличивать количе­ство торгуемых контрактов в среднем через каждые 10 сделок. Если для увеличения числа контрактов с одного до двух требуется провести 10 сделок, то 10 сделок потребуется и для того, чтобы увеличить число контрактов с 10 до 11 (в среднем):

Прибыль, требуемая для

увеличения числа контрактов до 2= $5.000

$5.000 / $500 =10 (среднее количество сделок)

Чтобы увеличить число контрактов 10 до 11, потребуется 50.000 прибыли:

10 контрактов х $5.000 = $50.000

Поскольку мы торгуем 10 контрактами, то наша прибыль, получа­емая от средней сделки, также должна быть умножена на 10. Поэтому уравнение будет иметь следующий вид:

$50.000 / $5.000 = 10 сделок

Таким образом, через 100 торговых сделок, в соответствии с наши­ми предположениями, у нас будет 10 контрактов. Если продолжить таблицу с дельтой в 5.000 долларов до 10 контрактов, она покажет, что $50.000 прибыли на один контракт должны дать приблизительно 225.000 долларов:

$85.000 + (6 х $5.000) = $115.000 $115.000 + (7 х $5.000) = $150.000 $150.000 + (8 х $5.000) = $190.000 $190.000 + (9 х $5.000) = $235.000

Вычтите начальное сальдо в 10.000 долларов и вы получите 225.000 прибыли! Очевидно, что все сделки не принесут одинакового дохода. Первые 50 сделок могут дать 35.000 долларов прибыли (в сред­нем 700 долларов на одну сделку), в то время как последующие 50 сде­лок дают 15.000 долларов прибыли (300 долларов на сделку). Нас не интересует точная сумма прибыли на сделку в среднем. Просто чем боль­ше средняя прибыль на сделку, тем быстрее растет число контрактов.

Тем не менее это только приблизительные вычисления. И они не могут быть точнее, поскольку мы не можем учитывать асимметричное действие рычага. Консервативные расчеты, производимые с учетом эффекта рычага, помогают определить приблизительно 90% предпола­гаемых прибылей. Для асимметричного рычага не существует матема­тической формулы, потому что он определяется исключительно на ос­новании последовательности сделок, как показано во второй главе.

После получения 100.000 долларов прибыли при помощи дельты 5.000 долларов мы можем увеличить число торгуемых контрактов до 20. Минимальный уровень прибыли для торговли 20 контрактами ра­вен 1.000.000 долларов. Таким образом, то, что за 4 года может прине­сти 225.000 долларов прибыли, может принести еще 750.000 долларов в последующие 4 года. Обратите внимание, что ставка сложных про­центов оставалась относительно неизменной: 225.000 долларов - это на 450% больше, чем тот доход, который можно было бы получить, тор­гуя одним контрактом в течение четырех лет. В то же время 1.000.000 долларов - это 400% от суммы в 225.000 долларов, если мы продолжим использовать этот метод в течение еще четырех лет. Общее увеличение по сравнению с результатами торговли, основанной на одном контрак­те, составляет 1.000%, или в 10 раз больше!

Мы обсудили потенциал прибыли, а теперь давайте рассмотрим фактор риска. При размере счета, равном 240.000 долларов и 10 торгу­емых контрактах, если произойдет убыток в сумме 5.000 долларов, то величина счета уменьшится до 194.000 долларов, или на 19%:

$240.000 при торговле 10 контрактами с $1.000 убытков = -$10.000

$240.000 - $10.000 = $230.000 при торговле 9 контрактами 9х(-$1.000) =-$9.000

$230.000 - $9.000 = $221.000 при торговле 9 контрактами 9х(-$1.000) =-$9.000

$221.000 - $9.000 = $212.000 при торговле 9 контрактами 9х(-$1.000) =-$9.000

$212.000 - $9.000 = $203.000 при торговле 9 контрактами 9х(-$1.000) =-$9.000

$203.000 - $9.000 = $194.000 при торговле 9 контрактами и при этом дальнейшее снижение счета остановлено

Если бы те же самые потери приходились на один контракт, то убыток по счету составил бы 8,3% от общей суммы счета. Таким обра­зом, прибыли возросли на 450%, в то время как риск вырос всего на 11%! Сопоставив размеры счета, чем бы вы рискнули: 10% от $60.000 или же 20% от $240.000? Понеся убытки, в первом случае вы бы сохра­нили 55.000 долларов, торгуя одиночным контрактом, а во втором -190.000 долларов после торговли по методу фиксированной пропор­ции. Все равно получается 350% роста.

Однако, в конечном счете, сравнение с Фиксированно-Фракцион­ным методом неизбежно. В этом сравнении используется схема торгов­ли "один контракт на каждые 10.000 долларов". При таком сценарии после получения 50.000 долларов прибыли на один контракт метод фиксированной пропорции обеспечивает рост до 830.000 долларов при 83 контрактах. После первого убытка в размере 1.000 долларов сумма счета уменьшилась бы на 83.000 долларов или до 747.000 долла­ров. После убытка по контракту на все 5.000 долларов сумма счета уменьшилась бы до 490.000 долларов. Это все же значительно больше, чем позволяет получить консервативный Фиксированно-Фракцион­ный метод, но тем не менее составляет 41% от предполагаемой суммы. Помимо этого, потери по контракту в размере 10.000 долларов приве­дут к "проседанию" счета до 291.000 долларов. Вы можете себе пред­ставить, что прибыль уменьшается с 830.000 долларов до 291.000 дол­ларов лишь из-за того, что цена торгуемого контракта уменьшилась на 10.000 долларов. Перспектива роста счета составила бы 52% величи­ны счета, а перспектива риска - 65%. Такое соотношение между рис­ком и вознаграждением явно не в пользу торгующего.

Кроме того, при 40.000 долларов прибыли (вместо 50.000) в тор­говле было бы занято 30 контрактов при размере счета всего 300.000 долларов. Это означает, чтопоследние 64% прибыли были получены только за счет предыдущих 20% прибыли. Если бы "проседание" счета в расчете на контракт произошло в этот момент, а не тогда, когда уро­вень прибыли достиг 50.000 долларов, то размер счета упал бы до 180.000 долларов и никакого роста бы не произошло.

Возможно, вы можете возразить, что 800.000 долларов стоят того, чтобы использовать Фиксированно-Фракционный метод, и вы готовы понести 41% потери при падении стоимости контракта на 5.000 долла­ров или принять 65% убыток при падении стоимости контракта на 10.000 долларов. Конечно же, верно, что при использовании Фиксиро­ванно-Фракционного метода вы можете получить более значительные прибыли за более короткий срок. Если вы преследуете именно эту цель, тогда торгуйте с использованием оптимальной фракции. Однако я го­ворил со многими трейдерами и выяснил, что никто не использует ме­тод оптимальной "ф" из-за убытков, которые он создает. Большинство просто не желают приближаться к 1.000.000 долларов, чтобы затем снова расстаться с 65% при падении. Помимо этого, выбранная дельта слишком консервативна для того, чтобы использовать ее при учете не­большого негативного развития цены в размере 5.000 долларов на кон­тракт. Уменьшив размер дельты до 2.500 долларов, те же самые 50.000 долларов дадут 485.000 долларов при торговле 20 контрактами, при­чем риск будет составлять всего 20% от этой суммы. После достижения 30.000 прибыли Фиксированно-Фракционный метод может принести всего 100.000 долларов, в то время как Фиксированно-Пропорциональ­ный метод при дельте 2.500 долларов при таких же условиях приносит 175.000 долларов. Негативное развитие ситуации в пределах 5.000 долларов на контракт при Фиксированно-Фракционном методе приве­дет к снижению счета до 60.000 долларов, а при методе фиксирован­ной пропорции величина счета уменьшилась бы до 122.500 долларов -почти вдвое больше!

Как видите, определенные компромиссы вполне возможны. Одна­ко принимая во внимание и риск, и вознаграждение, метод фиксиро­ванных пропорций предлагает баланс между этими двумя величина­ми. Убытки неизбежны, и они часто определяют, может трейдер про­должать торговлю или нет. Трейдер, который не может выдержать убытки, не сможет добиться высоких прибылей. Можно изменить стра­тегию, но это не поможет перейти из убытка в прибыль. Вы должны учитывать и риск, и вознаграждение при любом методе управления ка­питалом.

Это приводит нас еще к одному соотношению в рамках метода фиксированной пропорции. Как между дельтой и убытком, так и между дельтой и средней прибылью существует пропорциональная связь. На­пример, если дельта равна $5.000, а ожидаемое падение цены контрак­та составляет $10.000, то дельта будет пропорциональна убытку в соот­ношении 1:2. Производя изменения в одной части этого соотношения, необходимо произвести такие же изменения и в другой. Если вы поде­лите убыток на дельту (в этом случае получится 2), то это соотношение будет сохраняться всегда, вне зависимости оттого, каким числом кон­трактов будет исчисляться убыток. Сумма потерь на счете от убыточ­ной торговли будет равняться двум дельтам (или двум контрактам). Ес­ли я достигаю 10-контрактного уровня, используя дельту $5.000, а по­том теряю на "проседании" по $10.000 на контракт, то размер счета не упадет ниже, чем на два контрактных уровня. Поэтому после потерь я окажусь на уровне 8 контрактов. Если я торгую 10 контрактами с дель­той, равной 2.500 долларов, а "проседание" на контракт составляет $10.000, то в результате потерь величина счета упадет не ниже уровня 6 контрактов:

$10.000 снижение стоимости / $2.500 дельта = 4 дельта-уровня (контракта)

10-4 =6

Основное преимущество этой пропорций заключается в том, что вы знаете не только на каком уровне находитесь в данный момент вре­мени, но и размеры потенциального убытка в зависимости от исполь­зуемой вами дельты. Приводимая ниже формула определяет изменение уровня контрактов, лишая вас утомительной необходимости состав­лять таблицы:

[(число контрактов х число контрактов - число контрактов)/2] х дельта = минимальный уровень прибыли

Если число торгуемых контрактов равно 10, а дельта составляет 5.000 долларов, то минимальный уровень необходимой прибыли со­ставит 225.000 долларов:

10x10 = 100

100 - 10 = 90

90 / 2 = 45

45 х $5.000 =$225.000

На уровне прибыли в 225.000 долларов я могу перейти от 9 кон­трактов к 10 или от 10 к 9 контрактам в зависимости от того, в какую сто­рону изменится размер моего счета: увеличится или сократится.

Если вместо "- число контрактов" я подставлю "+ число контрак­тов", то получу верхний уровень для торговли 10 контрактами. Именно такая сумма позволит увеличить число контрактов от 10 до 11 или же, наоборот, уменьшить их с 11 до 10, в зависимости оттого, в какую сто­рону изменится размер моего счета:

10x10 = 100 100+ 10 =110

110/2 =55

55 х $5.000 =$275.000

Теперь я знаю нижний (225.000 долларов) и верхний (275.000 дол­ларов) уровни прибыли для 10-контрактной торговли. Их также можно рассматривать как верхний предел для торговли 9 контрактами и ниж­ний - для торговли 11 контрактами. Поскольку я могу рассчитать эти уровни, а также максимальную сумму "проседания" счета в случае убытков, то я знаю точную сумму риска в долларах на данный конкрет­ный момент времени. Если я торгую на уровне 250.000 долларов при­были, то мне известно, что если каждый контракт принесет потерь на 10.000 долларов, то размер моего счета не упадет ниже 8 контрактов.

8x8 =64

64-8 =56

56/2 =28

28 х $5.000 =$140.000

Это минимальный уровень прибыли, если счет "просядет" на 10.000 долларов в расчете на контракт. Однако если бы я хотел полу­чить более точные расчеты, то мне пришлось бы еще вычислить расстояние между 10- и 11-контрактным уровнями. Тогда я оказался бы в такой же ситуации выбора и в случае с 8 и 9 контрактами.

 

Сумма 250.000 долларов находится точно посередине между ниж­ним уровнем 225.000 долларов и верхним 275.000 долларов. Средняя величина между верхним и нижним уровнями торговли 8 контрактами составляет 160.000 долларов. Именно в этой точке мы окажемся в слу­чае падения счета в расчете на контракт:

10 х 10 / 2 х $5.000 = $250.000 8х8/2х$5.000 =$160.000

Подставляя в формулу "- число контрактов", мы вычислим нижний уровень. Подставляя "+ число контрактов", вычисляем верхний уро­вень. Поэтому, убирая из выражения "+" или "-", можно точно опреде­лить середину между двумя соседними уровнями. Опираясь на эти три точки, легко рассчитать размер счета на данный момент времени по сравнению с какой-либо иной величиной. Например, размер счета 230.000 долларов составляет 20% от точной середины. Поэтому следу­ет вычесть 80% от уровня торгуемых контрактов. Расчеты выглядят следующим образом:

10x0,80 =8 [(10хЮ-8)/2]х$5.000 =

46 х $5.000 =$230.000

Соответствующий убыток после развития цены в неблагоприят­ном направлении:

8x0.80 =6.4 [(8х8-6.4)/2]х$5.000 =

28 х $5.000 =$144.000

Этот метод позволяет вам точно рассчитать, каких убытков можно ожидать от.нескольких неудачных сделок подряд. А возможность пре­дугадать исход сражения - это уже половина победы.