Решение. Каждую вершину сети разбиваем на четыре сектора
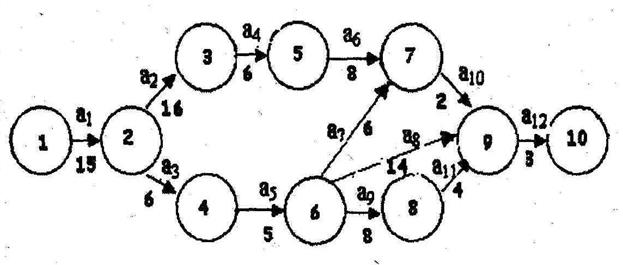
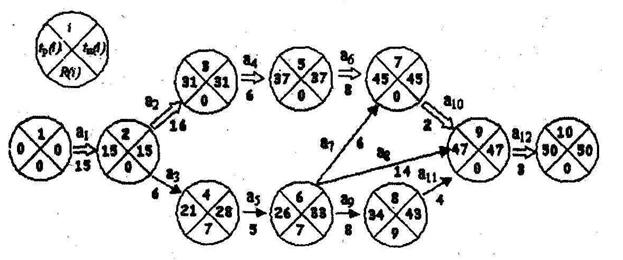
Каждую вершину сети разбиваем на четыре сектора. В верхней части сектора отмечается номер события i, в левой – ранний срок свершения события i, в правой – поздний срок свершения события i, в нижней – резерв времени этого события (рис. 8). Сначала по формуле (1) находим ранние сроки свершения события i и заносим их в левые секторы сетевого графика. Имеется:
Рисунок 7
Рисунок 8 tР (1)=0; tР (2)=0+15=15; tР (3)=15+16=31; tР (4)=15+6=21; tР (5)=31+6=37; tР (6)=21+5=26; tР (7)=max{37+8;26+6}=45; tР (8)=26+8=34; tР (9)= max{45+2;26+14;34+4}=47; tР (10)=47+3=50. Теперь рассчитываются поздние сроки свершения событий. Расчет начинается с последнего события и затем, «пятясь», двигается к первому событию. Для i=10 поздний срок свершения события tП (10)= tР (10)=47+3=50. Далее по формуле (2) имеется: tП (9)=50-3=47; tП (8)=47-4=43; tП (7)=47-2=45; tП (6)=min{45-6;47-14;43-8}=33; tП (5)=45-8=37; tП (4)=33-5=28; tП (3)=37-6=31; tП (2)= min{31-16;28-6}=15; tП (1)=15-15=0. Результаты расчета заносят в правые секторы вершин сети. По формуле (3) рассчитывают резервы времени каждого события и заносят их в нижние секторы вершин. Например: R(1) =0-0=0; R(2) =15-15=0; R(3) =31-31=0; R(4) =28-21=7 и т.д. Чтобы рассчитать критический путь фиксируются события, не имеющие резервов времени. Это события 1,2,3,5,7,9,10. Следовательно, путь 1→2→3→5→7→9→10 является критическим. Длина критического пути tКР= tР (10)=50. Критический путь отмечается на сетевом графике двойной стрелкой.
|