Решение. Чтобы найти указанные параметры работ, используем формулы (1) – (10), также результаты решения предыдущего примера

Чтобы найти указанные параметры работ, используем формулы (1) – (10), также результаты решения предыдущего примера, оформленные в виде сетевого графика (рис.8).

Результаты расчетов сведены в (табл. 2).

Графа 3 (табл. 2) заполняется с помощью сетевого графика (рис.8). Последовательно выписываются числа, стоящие в левых секторах кружков. Графу 4 (табл. 2) заполняют, складывая числа граф 2 и 3. Затем заполняется графа 6, выбирая последовательно числа из правых секторов кружков сетевого графика. Графа 7 равна разности граф 6 и 4. Графа 8 заполняется на основе формулы: R_С (i, j) = t_Р (j)- t_РО (i, j). Здесь числа t_Р (j) берутся из левых кружков графика 8, а t_РО (i, j) – из графы 4. Для работы а₁=(1,2). Она оканчивается в секторе кружка, моделирующего событие 2, поэтому t_Р (2) =15. Из графы 4 имеется t_РО (1,2)=15. Значит R_С (1,2) = 15-15=0. Для работы а₇=(6,7) имеется t_Р (7)=45; t_РО (6,7)=32. Поэтому R_С (6,7) = 45-32=13 и т.д. Выявляют всевозможные полные пути для выполнения работ комплекса, находят их длину, резервы времени.

Таблица 2 – Результаты расчетов сетевого графика

 

Работа	Продолжительность t (i, j)	Сроки выполнения	Резервы времени работ
Ранние	Поздние
Начало tРН (i, j)	Окончание tРО (i, j)	Начало tПН (i, j)	Окончание tПО (i, j)	Полный RП (i, j)	Свободный RС (i, j)
а1= (1,2)
а2= (2,3)
а3= (2,4)
а4= (3,5)
а5= (4,6)
а6= (5,7)
а7= (6,7)
а8= (6,9)
а9= (6,8)
а10= (7,9)
а11= (8,9)
а12= (9,10)

 

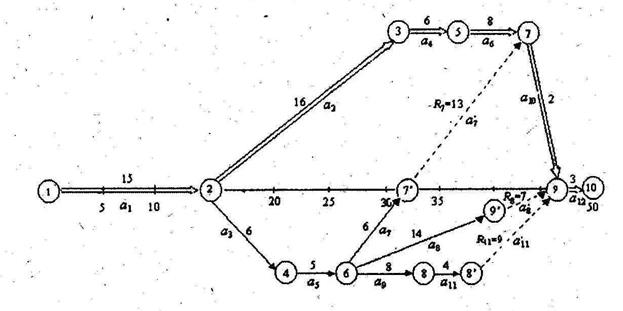
L₁:1→2→3→5→7→9→10 – критический путь

L₂: 1→2→4→6→7→9→10

L₃: 1→2→4→6→9→10

L₄: 1→2→4→6→8→9→10

Длина этих путей:

T₁=t(L₁)=t_КР = 15+16+6+8+2+3=50 дней

T₂=t(L₂)=15+6+5+6+2+3=37 дней

T₃=t(L₃)=15+6+5+14+3=43 дня

T₄=t(L₄)=15+6+5+8+4+3=41 день.

Таким образом, длительность максимального пути равна 50 дням, за это время все работы комплекса будут выполнены, то есть 50 дней – это минимальное время для выполнения всех работ комплекса.

Определяются резервы времени по выявленным путям, используя формулу (8):

R(L₁)= t_КР – T₁=0 дней;

R(L₂)= t_КР – T₂=50-37=13 дней

R(L₃)= t_КР – T₃=50-43=7 дней

R(L₄)= t_КР – T₄=50-41=9 дней.

В пределах имеющихся резервов времени общий срок выполнения работ не увеличивается, если не увеличилась длительность выполнения любой из работ критического пути.

Для наглядности выявления резервов времени строится график работ (рис.7) в масштабе времени. Построение начинается с критического пути L₁ в соответствие с правилами сетевого моделирования с учетом изображения длительности работ t₁ в масштабе времени по оси абсцисс. По оси ординат длина стрелок выбирается из соображений удобства восприятия сети в целом. Этим объясняется, например, большая длина стрелки работы а₁₀ по сравнению с а₆, хотя по масштабу времени t₆> t₁₀. В результате получается сетевой график (рис.9).

 

Рисунок 9 – Сетевой график работ в масштабе времени

При построении сетевого графика в масштабе времени сталкиваются с необходимостью введения фиктивных работ 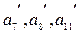(пунктирные стрелки) и фиктивных событий . Время выполнения этих фиктивных работ равно нулю, а их структура показывает расположение свободных резервов времени:

R₇= R_С(6,7)=13 дней

R₈= R_С(6,9)=7 дней

R₁₁= R_С(8,9)=9 дней.