Решение задачи минимизации общей продолжительности проекта
Сетевой график составляется после распределения всех ресурсов по каждой работе. Эти ресурсы определяют время выполнения работ. На сетевом графике не все работы критические. Поэтому можно уменьшить время Обозначим ресурсы по работам а1, а2…., соответственно b1, b2 …. Пусть работа аi со временем ее выполнения ti, лежит на критическом пути, а аk – некоторая работа, лежащая на некритическом пути, и время ее выполнения – tk. Механизм перераспределения средств включает уменьшение средств работы аk на некоторую величину xi< bk, что приводит к увеличению ее времени выполнения Средства xk, вложенные в работу аi, то есть xk= xi, приводят к уменьшению времени ее выполнения: В практике выполнения расчетов φ(xk) и
Обозначают Тогда формулы (14) примут вид:
При таких операциях должно выполняться условие: сумма снятых с некритических работ средств должна равняться сумме вложенных средств на критические работы: Общий срок выполнения всего комплекса работ определяется целевой функцией:
Здесь i – номера тех работ критического пути, средства которых не изменились. Требуется так перераспределить средства с некритических работ на критические, чтобы функция (15) приняла наименьшее значение. Сколько средств можно взять с некритической работы? Ясно, что все взять нельзя. Снимаемые средства определяют наличием резервов времени. Пусть свободный резерв времени работы аk равен RC (аk). Тогда должно выполняться условие tk xkск ≤ RC (аk), откуда xk≤ Замечание. Если снимаются средства с работы аk, лежащей на пути L, то нельзя вкладывать данные средства в другую работу, лежащую на этом пути, которая является также частью критического пути. Решение задачи оптимизации состоит в последовательном переносе средств с некритических работ на критические, переходе от одного пути к другому до тех пор, пока все работы не будут находиться на критических путях и иметь резервы. В этом случае длительность всех путей станет одинаковой. Пример Провести оптимизацию сетевого графика (рис.9) по критерию минимума времени выполнения всех работ комплекса; построить оптимальный сетевой план работ; определить экономию. При условии, что с1= 0,1; с2= 0,2; с3= 0,3; с4= 0,4; с5= 0,5; с6= 0,6; с7= 0,7; с8= 0,9; с9= 0,8; с10= 1,0; с11= 1,1; с12= 1,2.
|

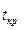 за счет резервов на некритические работы, можно уменьшить время их выполнения и тем самым получить новый срок выполнения работ, меньший
за счет резервов на некритические работы, можно уменьшить время их выполнения и тем самым получить новый срок выполнения работ, меньший 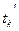 = φ(xk)> tk.
= φ(xk)> tk.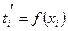 < tk.
< tk.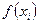 обычно представляют приближенными линейными выражениями вида:
обычно представляют приближенными линейными выражениями вида: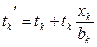 ;
;  (14)
(14)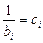 - коэффициент пересчета.
- коэффициент пересчета.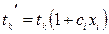 ;
; 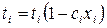
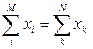 , где М – число работ, на которые средства вкладывались, а N – число работ, с которых средства снимались.
, где М – число работ, на которые средства вкладывались, а N – число работ, с которых средства снимались.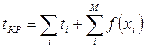 (15)
(15) - ограничение на снимаемые с работы аk средства.
- ограничение на снимаемые с работы аk средства.


