Решение. Максимальный путь, проходящий через работу а5= (4,6), - это путь
Максимальный путь, проходящий через работу а5= (4,6), - это путь L4: 1→2→4→6→8→9→10 t(LMAX)= t(L4)=43 дня. Несовпадающие отрезки этого пути и критического пути заключены между событиями 2 и 9. Для пути L4 – это отрезок 2→4→6→9; а для критического пути – отрезок 2→3→5→7→9. Отрезок пути L4, совпадающий с критическим путем, - это отрезки 1→2 и 9→10, длина Кi (i, j)= КН (i, j)= Коэффициент напряженности КН (i, j) может изменяться в пределах от 0 (для работ, у которых отрезки максимального из путей, не совпадающие с критическим путем, состоят из фиктивных работ нулевой продолжительности) до 1 (для работ критического пути). Чем ближе к 1 коэффициент напряженности, тем сложнее выполнять данную работу в установленные сроки, а чем ближе он к нулю, тем большим относительным резервом обладает максимальный путь, проходящий через данную работу. Работы могут обладать одинаковыми полными резервами, но разной степенью напряженности. И наоборот, различным полным резервам могут соответствовать одинаковые коэффициенты напряженности. Из формулы (13) видно, что величина коэффициента напряженности зависит от RП и
|

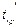 которого равна
которого равна  =50. Подставив найденные значения в формулу (12):
=50. Подставив найденные значения в формулу (12):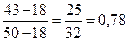 .
.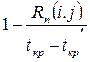 (13)
(13) . Чем полный резерв времени RП больше выполнения некоторой работы и
. Чем полный резерв времени RП больше выполнения некоторой работы и  , (то есть чем меньше
, (то есть чем меньше 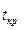 -
-  - отрезок времени максимального пути, проходящего через эту работу и не совпадающего с критическим путем), тем больше будет дробь, стоящая в правой части формулы (13), и тем меньше коэффициент напряженности этой работы, тем легче будет ее выполнить. В общем случае указанная дробь определяет удельный вес полных резервов времени работ в продолжительности отрезков максимальных путей, не совпадающих с критическим путем. Чем больше этот удельный вес, тем меньше коэффициент напряженности.
- отрезок времени максимального пути, проходящего через эту работу и не совпадающего с критическим путем), тем больше будет дробь, стоящая в правой части формулы (13), и тем меньше коэффициент напряженности этой работы, тем легче будет ее выполнить. В общем случае указанная дробь определяет удельный вес полных резервов времени работ в продолжительности отрезков максимальных путей, не совпадающих с критическим путем. Чем больше этот удельный вес, тем меньше коэффициент напряженности.


