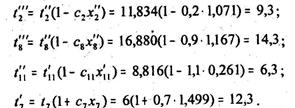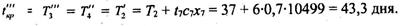Решение. Выявленные свободные резервы позволяют провести оптимизацию сетевого графика, связанную с лучшим перераспределением выделенных ресурсов
Выявленные свободные резервы позволяют провести оптимизацию сетевого графика, связанную с лучшим перераспределением выделенных ресурсов, и построить план выполнения всего комплекса работ за меньшее время, то есть более экономный. Оптимизацию сетевого графика проводят путем переноса части средств с некритических работ на критические, фиксируя при этом номера работ, с которых средства снимаются и на которые переносятся. Переносятся резервы с некритических работ на критические, будут увеличивать некритический путь и уменьшать критический до тех пор, пока не совпадут длительность всех путей. Располагают длительность всех путей последовательно в порядке увеличения их резервов и начинают оптимизацию с первой пары путей L1,L3. На первом этапе оптимизации переносим резервы с некритического пути L3 некритические работы а8, имеющей свободный резерв времени R8=RC (а8)=7. Берется часть средств x8 работы а8 и переносятся на работу а2 критического пути. Эти средства на работе а2 обозначим x2. Тогда длительность новых критических путей: Величину переносимых средств x8 можно определить, решив систему:
При ограничении По условию: T1= 50; T3= 43; с2= 0,2; t2 =16; с8= 0,9; t8 =14; R8= 7. Поэтому система (16) примет вид:
Отсюда: x8 =0,443. Ограничение Новое время выполнения работ а8, а2 находятся по формулам: Имеется:
На втором этапе рассматривается следующий ближайший некритический путь L4, на котором у работы а11 имеется свободный резерв времени:
Снимаемая с работы а11 часть средств x11 должна удовлетворять условию: Средства x11 переносятся на работу а2 в количестве Для нахождения величин переносимых средств составляют систему уравнений:
Подставив в систему (17): с2 =0,2; Имеют:
Следовательно, x11 = 1,098; Ограничение Новое время выполнения работ а2, а8, а11 находим по формулам:
Имеют:
Новый критический путь:
На третьем этапе рассматривают на последнем пути L2 наличие резерва времени у работы а7. Свободный резерв времени у работы а7 равен:
Снимают средства x7 и записывают условие допустимости
Решая эту систему при числовых данных: с2 =0,2; с8 =0,9; с11 =1,1; с7 =0,7; t7 = 6; Получается:
Ограничение Новое время выполнения работ а2, а8, а11, а7 вычисляется по формулам:
Новый критический путь:
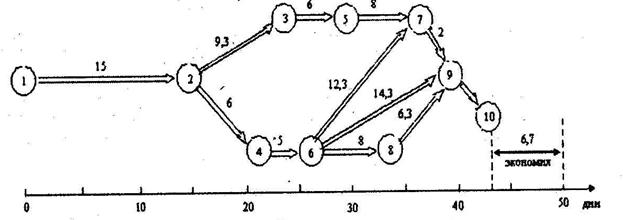
Экономия 50 – 43,7 = 6,7 дня. Строят оптимальный план работ (рис.10).
Рисунок 10 – Оптимальный календарный план
|

 <
< 
 (16)
(16)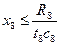

 выполнено.
выполнено.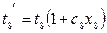 ;
;  ; новый критический срок
; новый критический срок  .
.

 .
.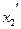 и на работу а8 в размере
и на работу а8 в размере  для ускорения выполнения работ первого и третьего путей.
для ускорения выполнения работ первого и третьего путей.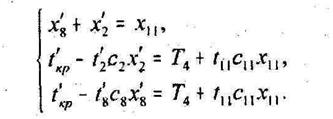 (17)
(17) 14,592; с8 =0,9;
14,592; с8 =0,9; 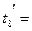 19,582;
19,582;  48,583; T4 = 41; с11 = 1,1; t11 = 4.
48,583; T4 = 41; с11 = 1,1; t11 = 4.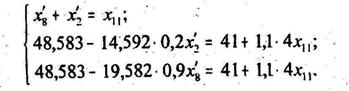
 0,154;
0,154;  0,944.
0,944. =
= 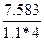 >1,098= x11 выполнено.
>1,098= x11 выполнено.



 . Переносим резервы x7 некритической работы а7 на работы а2, а8, а11 остальных критических путей в размерах
. Переносим резервы x7 некритической работы а7 на работы а2, а8, а11 остальных критических путей в размерах  ,
,  ,
,  соответственно и составляют систему уравнений:
соответственно и составляют систему уравнений: (18)
(18) 11,834;
11,834; 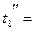 16,880;
16,880;  8,816;
8,816; 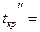 45,831; T2 = 37.
45,831; T2 = 37.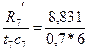 >1,499= x7 выполнено.
>1,499= x7 выполнено.