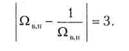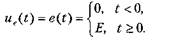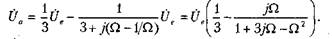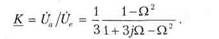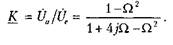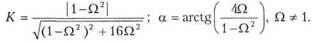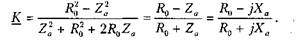ПРИМЕЧАНИЕ
Дифференцирующая цепь позволяет сформировать импульс отрицательного напряжения в цепи, где действуют исключительно источники положительных напряжений. Чтобы в этом убедиться, представьте форму напряжения на выходе RC-ueim при подаче на ее вход прямоугольного импульса положительной полярности. Неискажающий делитель напряжения Задумаемся над тем, как избежать искажения сигналов интегрирующими цепями. Дело в том, что в электронике цепи, способные при определенных условиях проинтегрировать сигнал, образуются естественным образом, поскольку в реальности двум проводникам или двум выводам всегда присуща некая емкость — межэлектродная, или монтажная, или емкость соединительного кабеля. Эта емкость может оказаться настолько малой, что постоянная времени образованной при ее участии цепи будет заметно меньше характерного времени измерений. Тогда емкостную реакцию в расчет не принимают. Если она и скажется на сигнале, это, как выше указывалось, проявится в малой задержке. В обратном случае, когда характерное время изменения сигнала соизмеримо с постоянной времени цепи, искажения сигнала становятся весьма заметными. С подобной проблемой сталкиваются при электротехнических измерениях. Входные зажимы (клеммы) любого измерителя характеризуются емкостной реакцией. Например, эквивалентную схему входа осциллографа, применяемого для наблюдения процессов, частота колебания которых не превышает несколько мегагерц, можно представить параллельным соединением двух элементов: сопротивления, приблизительно равного 1 МОм, и емкости 20-30 пФ. Если для подключения осциллографа используют коаксиальный кабель длиной около одного метра, к входной емкости осциллографа добавляется еще и емкость кабеля. Ее значение может составлять 200-300 пФ. В результате измеритель, который в идеале не должен влиять на процессы в исследуемых цепях, может исказить (проинтегрировать) быстро меняющий сигнал. И на экране отобразится ложная информация. ПРИМЕР В цифровой электронике при быстрых переключениях сталкиваются с появлением в проводах помехи, имеющей форму очень узких импульсов. Настолько узких, что в обиходе их называют «иголками». Такая иголка может нарушить логику работы устройства. Например, ее сосчитает счетчик, приняв за информационный импульс. Проблема состоит в том, что обнаружить иголку с помощью не приспособленного для высокочастотных измерений осциллографа непросто. Предположим, что длительность иголки заметно меньше постоянной времени цепи, образованной соединительным кабелем и входными клеммами осциллографа. Иголка «проинтегрируется» входной цепью осциллографа, и в результате на его экране появится едва заметный треугольник, который может затеряться на фоне «дрожащего» луча. Можно подключать измерительный прибор через низкоомный делитель на резисторах (см. рис. 3.12, а), такой, что сопротивление, параллельное проводникам соединительного кабеля (R2 на рис. 3.12, а), окажется на рабочих частотах существенно меньше емкостного сопротивления входных контактов осциллографа. И тогда влияние входной емкости будет ослаблено. Другой прием, позволяющий уменьшить искажения сигналов паразитными емкостями, состоит в использовании при высокочастотных измерениях неискажающего делителя напряжения (рис. 3.23). Его называют также компенсированным делителем напряжения. Ранее указывалось, что коэффициент передачи такой схемы не зависит от частоты при условии, что комплексные сопротивления Z, и Z2 (см. рис. 3.12, б) на любой частоте находятся в соотношении: Z2 = Z,y, где у является постоянным числом. Отсюда вытекает формула, связывающая значения элементов делителя, показанного на рис. 3.23: C{R\ = C2R2 или CJC2 = RJR2- Входное сопротивление такого делителя (ZBX) оказывается равным:
Эта формула дает основание представить входные контакты делителя эквивалентным двухполюсником, образованным параллельно соединенными элементами: сопротивлением /?, (1 + у) и емкостью С,/(1 + у). Таким образом, неискажающий делитель напряжения позволяет увеличить эквивалентное входное сопротивление и уменьшить эквивалентную входную емкость измерителя.
ПРИМЕР К входу осциллографа подключен коаксиальный кабель длиною 1 м. Эквивалентная схема контактов кабеля представляется параллельным соединением сопротивления 1 МОм и емкости 270 пФ. Смонтируем на конце кабеля щуп, соединив параллельно резистор, имеющий сопротивление 9 МОм, и конденсатор, имеющий емкость 30 пФ. В результате образуется делитель (см. рис. 3.23) с элементами: С, = 30 пФ, R, = 9 МОм, С2 = 270 пФ, R2= 1 МОм, и коэффициентом у = 1/9. Коэффициент деления напряжения оказывается равным: у/(1+у) = 0,1. Поскольку для элементов делителя выполняется условие C,-R, = C2R2, сигнал не должен искажаться. Эквивалентная схема входа осциллографа, оборудованного кабелем со щупом, состоит теперь из параллельно соединенных элементов: сопротивления R,(l + у) = 10 МОм и емкости С,/(1 + у) = 27 пФ. Таким образом, влияние контактов осциллографа на исследуемую цепь в заметной степени ослаблено. Но делитель ослабит и сигнал, поступающий на вход осциллографа, поэтому придется увеличить коэффициент усиления канала осциллографа. Однако на форме сигнала это уже не скажется. Частотные свойства полосового RC-фильтра Цепь, построенная по схеме, приведенной на рис. 3.24, является полоснопропускающим фильтром (сокращенно — ППФ). Чтобы в этом убедиться, получим выражения для коэффициента передачи и построим частотные характеристики данной цепи. На схеме замещения для комплексных амплитуд эта цепь выглядит как делитель, составленный из комплексных сопротивлений Zt и Z2 (см. рис. 3.12, б), причем: 1 /? /.. — Кл -----: z о =-----------. 1 j&C 1 + jaRC
Следовательно, для коэффициента передачи К =Ua/Ue получаем выражение:
Формулы для модуля коэффициента передачи и его аргумента (а значит, и для АЧХ и ФЧХ) имеют следующий вид:
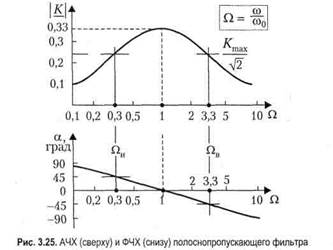
Для упрощения вычислений удобно перейти к новой переменной Q = &RC. По сути она является нормированной (отнесенной к 1/(RC)) частотой. В результате преобразований приходим к следующей формуле для коэффициента передачи: Из этих формул видно, что при Q -» 0 и при Q -> оо выходное напряжение ослабляется, поскольку |Q-1/Q|—>со. При П=1, то есть при со = l/(i?C) знаменатель выражения для К становится минимальным, и это означает, что на частоте со = 1/(RC) модуль коэффициента передачи максимален и равен 1/3. На этой частоте аргумент коэффициента передачи а = 0. Следовательно, выходное напряжение при со = 1/(RC) синфазно входному. Данную частоту (далее будем обозначать ее со0) называют квазирезонансной. Теперь видно, что D. — есть частота, нормированная к квазирезонансной частоте: Q = со/со0. Введем обозначение для нормированной квазирезонансной частоты: Q0 = Q(co0). Понятно, что Q0= 1. На рис. 3.25 приведены графики АЧХ и ФЧХ рассматриваемой схемы. Вид АЧХ наглядно демонстрирует, что схема, изображенная на рис. 3.24, является полосно-пропускающим фильтром. Границы полосы пропускания — верхнюю (Ц,) и нижнюю (Q„) частоты среза — найдем на основании формулы: К(с1ви) = /Cmax/v2 = = (1/3)/V2, из которой следует:
Отсюда находим значения границ полосы пропускания: QH= 0,3; Qn= 3,3 или со„= 0,3со0; сов = 3,3со0. Вычислим также относительную ширину полосы пропускания — характеристику, по значению которой оценивают избирательность цепей. Она получается равной: (ю„- со,,)/со0 = 3.
По «радиотехническим меркам» относительная ширина полосы пропускания полосового ЛС-фильтра получилась очень большой. Приходится заключить, что такой фильтр не обладает достаточно высокой избирательностью, требуемой для решения многих практических задач. В частности, для избирательного приема радиостанций FM-диапазона, несущие частоты которых могут располагаться с интервалом (минимально допустимым) 120 кГц, требуется обеспечивать намного более высокую избирательность радиоприемных устройств. Относительная ширина полосы пропускания входных трактов радиоприемников должна составлять доли процентов. И в этой связи, казалось бы, полосовой 7?С-фильтр должен иметь узкую область применения. Однако схема, содержащая только сопротивления и емкости, весьма привлекательна при создании устройств на базе интегральных технологий. Встраивание подобных ДС-фильтров в интегральные транзисторные цепи позволяет создавать на их основе устройства, характеризуемые высокой избирательностью. Переходная характеристика полосового RC-фильтра Подключим к полосовому.RC-фильтру (см. рис. 3.24) источник ЭДС, вырабатывающий в нулевой момент времени напряжение в форме ступенчатого скачка:
Будем считать, что напряжение на емкостях в исходном состоянии равно нулю. Поскольку форма входного напряжения отвечает функции Хевисайда, выходное напряжение ua(t) воспроизведет переходную характеристику цепи, так как: h(t) = ua(t)/E.
Получим уравнение, которому должно удовлетворять напряжение иа. Для тока i (см. рис. 3.24) можно записать: i = Си' + и JR. (Здесь и далее используется об-
1 "1 - К = К + ~р^иа + CRu"a + иа. Учитывая, что при t > 0 и'е = О, приходим к дифференциальному уравнению второго порядка для функции ua(t):
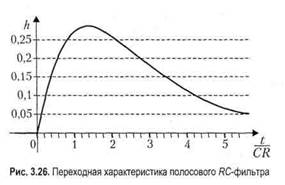
и"а +2Ъи'а +(о20иа = 0. (3.5) Его следует снабдить двумя начальными условиями, которые формулируются на основании непрерывности напряжений на емкостях. В данном случае это означает, что сразу после скачка входного напряжения (в момент времени t = +0) напряжения на емкостях останутся нулевыми. Отсюда следует: ua(t + 0) = 0; u'a(t + Q) = E/(CR). С учетом первого начального условия общее решение уравнения (3.5) можно искать в виде:иа = Л(ем - е7"2'). Коэффициенты Х1 и Х2 являются корнями характеристического уравнения: A.2 + 2S;v+co2 = 0. Они получаются такими: ^12=-8±V52-^ = -5±5у; у =jl-(o>J8)2. Теперь решение дифференциального уравнения принимает вид: ua(t) = 2Ae'&'sh(5yt). Выражение для коэффициента А найдем, воспользовавшись вторым начальным условием: и'а (+0) = (25уЛе"5' ch(8yO)( = (2/3) 8Е. Здесь использовано то, что со0/5 = 2/3. Поскольку у = л/5~/3, получаем: А = E/JE. Теперь ясно, как должно выглядеть выражение для выходного напряжения иа. Переходная характеристика полосового 7?С-фильтра имеет такой вид:
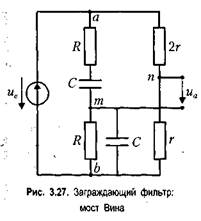
Заграждающий RC-фильтр (мост Вина) Заграждающий фильтр можно построить на базе полосового фильтра. Таковой является цепь, изображенная на рис. 3.27. Структурно эта схема относится к мостовым, отсюда ее название — мост Вина (в некоторых источниках — мост Вина—Робинсона). Источник входного напряжения включают в одну диагональ моста, выходное напряжение снимают с другой диагонали.
Левые плечи моста на рисунке представляют собой полосовой 7?С-фильтр, правые — делитель на сопротивлениях с коэффициентом передачи 1/3. Поскольку при гармоническом воздействии на квазирезонансной частоте со0 = 1/(RC) выходное напряжение полосового ЙС-фильтра синфазно входному и ослаблено в три раза, потенциалы полюсов тип «выходной» диагонали моста на этой частоте будут одинаковы. Так как выходное напряжение фильтра равно разнице этих потенциалов, оно станет нулевым. Это означает, что гармоническое напряжение, имеющее частоту со0 = 1/(RC), будет подавлено. Рассмотрим подробно свойства моста Вина в частотной области, а именно перейдем к комплексным амплитудам, вычислим передаточную функцию, построим АЧХ и ФЧХ. Для упрощения вычислений перейдем к нормированной частоте: Q = coRC = (u/a0. Выходное напряжение моста Вина равно разнице напряжений на выходе делителя и на выходе полосового ДС-фильтра. Следовательно, для комплексных амплитуд, воспользовавшись (3.4), можно записать:
Формулы для модуля коэффициента передачи и его аргумента (для АЧХ и ФЧХ) имеют следующий вид:
На рис. 3.28 приведены графики АЧХ и ФЧХ моста Вина. Форма АЧХ демонстрирует, что данная цепь является полоснозаграждающим фильтром.
Не составляет большого труда получить переходную характеристику моста Вина. Она, как можно увидеть из схемы цепи (см. рис. 3.27), находится вычитанием
переходной характеристики полосового.RC-фильтра из такой же характеристики делителя на сопротивлениях, равной 1/3: 3 V5 [2 RC) График этой функции приведен на рис. 3.29. Поскольку в нулевой момент времени переходная характеристика изменяется скачком, импульсная характеристика этой цепи не существует.
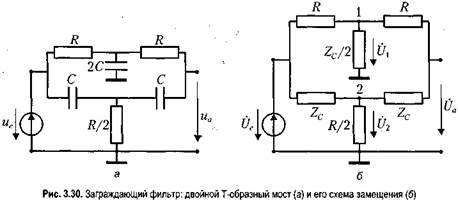
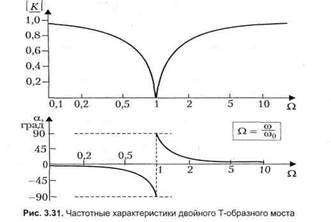
Заграждающий RC-фильтр (двойной Т-образный мост) Заграждающие фильтры можно строить по схеме, называемой двойным Т-образным мостом (рис. 3.30, а). На очень высокой частоте (как далее будет показано, значительно превышающей частоту со0 = 1/(RC)) гармонические колебания практически без ослабления пройдут на выход по «емкостному мостику» (нижнему на рисунке). На очень низкой частоте (со <к со,,) гармонические колебания также пройдут на выход, но уже по другому «мостику» (верхнему на рисунке). Гармоническое напряжение, имеющее частоту со0 = 1/(RC), будет подавляться. Чтобы в этом убедиться, перейдем к схеме замещения для комплексных амплитуд (рис. 3.30, б), вычислим передаточную функцию, построим АЧХ и ФЧХ. Нужно иметь в виду, что на схеме замещения Zc — комплексное сопротивление емкости С, равное: Zc = -j/(&C). Введем также нормированную частоту: Q = &RC = со/со0.
Комплексная амплитуда выходного напряжения связана с £7, и й2 выражением:
После их решения обратимся к формуле Ua = U2 + (£/, - U2)/(l + jd.) и найдем коэффициент передачи К = Ua /Ue. Он оказывается равным:
Формулы для модуля коэффициента передачи и его аргумента (для АЧХ и ФЧХ) имеют следующий вид:
Заграждающие фильтры используют не только для подавления колебаний некоей полосы частот. Как это ни покажется странным, на их основе строят и частотно-избирательные цепи, выполняющие функцию полоснопропускающих фильтров. Фазосдвигающие цепи, фазовый корректор Существуют линейные цепи, которые сдвигают по фазе гармоническое напряжение, не изменяя при этом его амплитуду. Такими свойствами обладает мостовой (другое наименование — скрещенный) симметричный четырехполюсник, схемы замещения которого в разных вариантах начертания показаны на рис. 3.32. Выясним, какие элементы следует включить в плечи моста, чтобы цепь выполняла заданный сдвиг фазы, но не изменяла при этом амплитуду напряжения, подаваемого на вход.
При описании свойств линейных четырехполюсников в частотной области используют (см. например [14]) понятие характеристического сопротивления (обозначим его Z0). Оно обладает такой особенностью: если выходные полюсы симметричного четырехполюсника нагрузить сопротивлением, равным характеристическому, входное сопротивление нагруженного таким образом четырехполюсника окажется равным этому же значению (Z0). Четырехполюсник, к выходу которого подключено сопротивление, равное характеристическому, называют согласованным. Характеристическое сопротивление симметричного четырехполюсника определяют по результатам расчета (или измерения) входного импеданса при двух разных состояниях выходных полюсов — короткозамкнутом и разомкнутом. Пусть ZKi — сопротивление между полюсами (входными) одной диагонали симметричного моста при коротком замыкании полюсов (выходных) другой, a Zxx — входное сопротивление в режиме холостого хода на выходе. Характерис тическ ое сопротивление связано с импедансами ZK3 и Zxx соотношением: Z0 = *JZKiZ^. Для моста, представленного на рис. 3.32, несложно вычислить ZKi, Zxx и далее Z0:
Отсюда следует, что модуль передаточной функции равен 1 и не зависит от частоты:
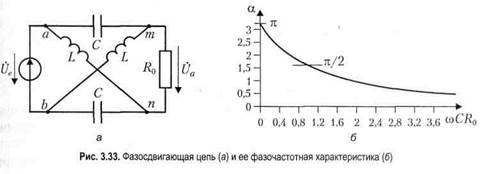
Конкретизируем схему — считаем, что Ха = -1/(соС), a Xb = со! (рис. 3.33, а). Тогда характеристическое сопротивление получается таким: R0 = -JbfC. Поскольку оно не зависит от частоты, не составит особой проблемы реализовать режим согласования, подключив к полюсам выходной диагонали моста резистор, имеющий именно такое сопротивление. При этом модуль передаточной функции на всех частотах будет равен единице, а для аргумента получаем формулу:
Фазочастотная характеристика, соответствующая данному примеру, показана на рис. 3.33, б. Подбирая значения элементов схемы С и L, можно обеспечить требуемый фазовый сдвиг на заданной частоте.
|