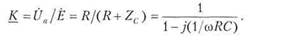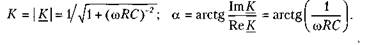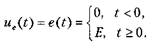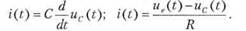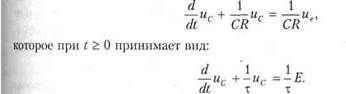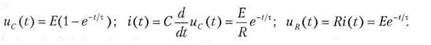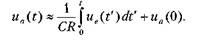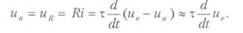ПРИМЕЧАНИЕ. Соединение двух асимптот фазочастотной характеристики наклонной прямой так, как показано на рис
Соединение двух асимптот фазочастотной характеристики наклонной прямой так, как показано на рис. 3.14 (тонкая линия), дает ошибку, не превышающую 6°.
Для колебаний, частоты которых находятся в полосе подавления, причем на значительном удалении от частоты среза сос, комплексные амплитуды выходных напряжений равны: Ua = ЁК» -Eja>c /со. Возврат к гармоническим функциям дает такую связь входного и выходного напряжений: Несложно увидеть, что выходное напряжение оказалось пропорционально интегралу от входного напряжения. Это обстоятельство дает основание называть.RC-цепь, у которой выходное напряжение снимается с емкости, интегрирующей цепью. Частотные свойства RC-цепи, включенной по схеме фильтра верхних частот
Выясним фильтрующие свойства цепи, схема которой приведена на рис. 3.15, а. Она также состоит из сопротивления R и емкости С, однако выходным напряжением иа здесь является напряжение на сопротивлении. Снова считаем, что источник ЭДС, подключенный к входу цепи, вырабатывает гармоническое напряжение: e(t) = E cos ((at). Его комплексная амплитуда равна: Ё = Е Схема замещения цепи (рис. 3.15, а) структурно представляет собой делитель на сопротивлениях. Коэффициент передачи (передаточная функция) этой цепи находится по формуле: Для модуля и аргумента коэффициента передачи получаем формулы:
Видим, что при со -> 0 выходное напряжение ослабляется пропорционально частоте (К(ю) «a>RC) и приобретает положительный квадратурный фазовый сдвиг. На высоких частотах (при со — > <») выходное напряжение не ослабляется (К» 1) и совпадает по фазе с входным (а» 0). Таким образом, данная цепь пропускает без ослабления колебания высоких частот и подавляет колебания низких частот. Следовательно, она является фильтром верхних частот. Основываясь на формуле К((йс) = Km.dX /v2 = 1/V2» 0,707, найдем границу (частоту среза со,), разделяющую полосы пропускания и подавления: сос = 1/(RC). На частоте среза фазовый сдвиг выходного напряжения по отношению к входному составляет л/4: а = arctg(l) = л/4. Перепишем полученные ранее выражения, введя в них сос:
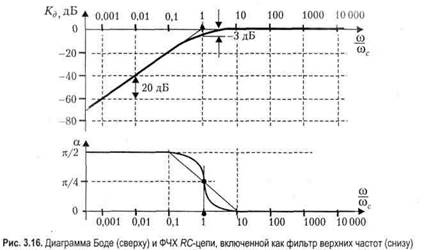
По этим формулам можно построить АЧХ — график функции К(а>), и ФЧХ — график функции а(со). Отметим характер асимптотического поведения АЧХ и ФЧХ в полосе подавления (при ю/сос «1) и в полосе прозрачности (при со/сос» 1): К» jco/cor, К ~ со/сос, а «л/2 при со/сос «1; На рис. 3.16 построены диаграмма Боде и ФЧХ данного фильтра верхних частот. Отметим, что в полосе пропускания асимптота коэффициента передачи проходит по оси абсцисс, а в полосе подавления асимптотой является прямая, имеющая наклон 20 дБ/дек (дек — декада) или 6 дБ/окт (окт — октава). Пересекаются асимптоты на частоте среза, на которой Кд = -3 дБ.
Переходные характеристики RC-цепи, импульсная характеристика Вычислим переходные характеристики.RC-цепи (рис. 3.17). Полагая, что напряжение на емкости в исходном состоянии отсутствует, рассмотрим воздействие на цепь в нулевой момент времени ЭДС в форме ступенчатого скачка:
Найдем ток в цепи (г) и напряжения на элементах (uR и ис). Поделив эти величины на Е, получим соответствующие переходные характеристики цепи.
Ток в рассматриваемой цепи связан с напряжениями на элементах следующими формулами:
Из них вытекает, что напряжение на емкости ис удовлетворяет дифференциальному уравнению:
Соответствующие переходные характеристики получаются такими:
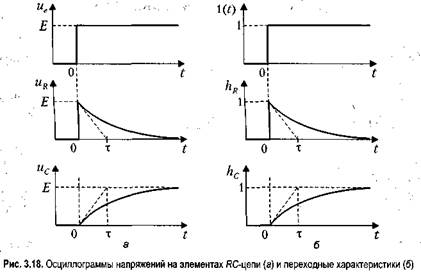
Поскольку импульсная характеристика находится дифференцированием переходной характеристики, констатируем, что таковая в данной цепи существуег1 только для емкости. Она равна: На рис. 3.18, а приведены графики поведения во времени входного напряжения ие, а также напряжений на емкости и сопротивлении. Кривую uR можно считать графиком тока, поскольку ток изменяется так же, как uR. По сути приведенные кривые являются графиками разных переходных характеристик. Они показаны на рис. 3.18, б.
Величина т задает скорость изменения переходных характеристик во времени. Эту величину называют постоянной времени. Ее можно найти из осциллограмм напряжений на элементах. На рис. 3.18, а проведена касательная функции uR при t = + 0. Она отсекает на оси абсцисс отрезок, длина которого как раз равна постоянной времени т. При t = т напряжение на выходе отличается от предельного значения, к которому стремится соответствующий отклик, примерно на 37 %. При описании цепи во временной области постоянная времени играет ту же роль, что и граничная частота при описании цепи в частотной области. Они связаны очевидным соотношением: т = 1/сас. Таким образом, по найденному из осциллограмм значению постоянной времени можно вычислить частоту среза. И это означает, что поведение цепи в частотной области можно описать по результатам измерений во временной области. В том числе можно построить АЧХ и ФЧХ цепи. И наоборот, зная частотные характеристики, можно предсказать поведение осциллограмм тока в цепи и напряжений на элементах. Когда ЙС-'цепь описывалась в частотной области, обращалось внимание на сугубо разную реакцию в зависимости от соотношения граничной частоты (частоты среза) и частоты внешнего воздействия. Подобный анализ, выявляющий влияние значения т на временные отклики цепи, стоит провести и в данном случае. Для этого введем некий условный временной параметр Т, который будем называть характерным временем наблюдаемого (измеряемого) процесса. Его можно ассоциировать, например, с периодом развертки осциллографа или, выражаясь иначе, с временем движения пятна луча по горизонтали. А можно в качестве характерного времени наблюдения Т рассматривать период колебаний, поступающих на вход цепи. Соотнося значения Гит, удается предсказывать эволюцию сигнала, прошедшего через цепь. Об этом идет речь далее.
Интегрирующая цепь Рассмотрим вариант использования в качестве выходных полюсов ЯС-цепи контактов емкости (рис. 3.19, а). В данном случае выходное напряжение иа совпадает с напряжением на емкости ис, а переходная характеристика цепи имеет вид: h(t) = 1-е~'/х. Предположим, что на вход цепи подается прямоугольное колебание — периодическая (с периодом Т) последовательность прямоугольных импульсов длительностью Т/2. В зависимости от соотношения постоянной времени т = RC и периода Т напряжение на выходе цепи будет существенно различаться по форме.
На рис. 3.19, б приведены осциллограммы напряжений иа для разных случаев. Видно, что при т «Т выходное напряжение мало отличается по форме от входного. Можно считать, что в случае малой по сравнению с характерным временем процесса постоянной времени т напряжение, поступающее на вход, практически не искажается. В другом крайнем случае, а именно при т» Т, цепь практически преобразует прямоугольное колебание в треугольное. Этот эффект можно пояснить, обратившись к выражению для напряжения на емкости. Поскольку в пределах половины периода колебаний входного напряжения справедливо неравенство t/x «1, при вычислении выходного напряжения допустимо пользоваться приближенным представлением экспоненциальной функции. В результате получаем: иа (О = Е(1 - е~ф) «£(1 -1 + t/x) = Et/x. Такая реакция — линейный отклик на ступенчатый перепад — дает основание называть рассматриваемую цепь интегрирующей. К тому же, если перейти к частотным характеристикам, из соотношения т» Т получаем: сос <к 2п/Т. Это означает, что частота следований входных импульсов, равная 1/Г, находится на оси частот правее частоты среза АЧХ. Следовательно, все гармоники, из которых состоит Из нее следует, что выходное напряжение является интегралом входного:
входное воздействие, попадают в полосу заграждения фильтра нижних частот и ослабляются. На этом основании можно считать выходное напряжение малым по сравнению с входным: иа <к ие. В результате приходим к приближенной формуле: График этой функции показан на рис. 3.20.
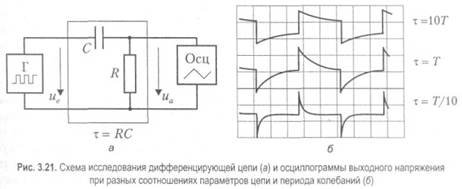
Временные рамки, в пределах которых рассматриваемая RC-цепь является интегрирующей, можно выявить, изучая реакцию цепи на линейно растущее входное напряжение. Пусть ие= at, где а — константа. Воспользовавшись интегралом Дюамеля, найдем выражение для выходного напряжения: Если т» t, получаем: ua(t) = at-ax(\-e~'lx)» at -at+ 0,5 at2/г = 0,5at2/x. Видно, что выходное напряжение пропорционально интегралу входного напряжения. В другом крайнем случае при т «: t получаем: ua(t)» a(t-x). Выходное напряжение повторяет входное с задержкой на интервал т. Таким образом, для малых по сравнению с т значений времени цепь можно считать интегрирующей. По мере увеличения времени точность интегрирования падает, и при t, заметно превосходящем т, влияние цепи коренным образом меняется — она задерживает входное напряжение. Дифференцирующая цепь Теперь рассмотрим вариант RC-цетт, у которой выходными полюсами являются контакты сопротивления, то есть цепь включена по схеме фильтра верхних частот (рис. 3.21, а). В данном случае выходное напряжение ua = uR,a переходная характеристика цепи имеет вид: h{t) = e't/x. При подаче на вход цепи прямоугольного колебания с периодом Г форма выходного напряжения на сопротивлении эудет зависеть от соотношения Т и t = RC. На рис. 3.21, б приведены осциллограммы напряжений иа для разных случаев. По сравнению с интегрирующей цепью ситуация на выходе при разных соотношениях Гит будет обратной. А именно, при х» Т выходное напряжение мало отличается по форме от входного. Можно считать, что при большом по сравнению с характерным временем процесса произведении RC напряжение, поступающее на вход, практически не искажается. В другом крайнем случае, а именно при х «Т, цепь радикально меняет форму входного напряжения — скачок входного напряжения «прозрачно» передается на выход, а затем выходное напряжение экспоненциально убывает и по истечении времени, равного нескольким х, становится нулевым. (При t=3x оно составляет менее 5 % входного скачка.)
Если обратиться к частотному описанию цепи, из соотношения х «к Т получаем, что частота среза АЧХ рассматриваемой цепи (а она является фильтром верхних частот) значительно превышает частоту повторения входных скачков (2тг/7), то есть сос» 2п/Т. Это означает, что гармоники, составляющие входное воздействие, в основном попадают в полосу заграждения фильтра верхних частот. На этом основании можно считать, что по истечении времени, заметно превышающего х, выходное напряжение будет мало по сравнению с входным: иа<а ие. Отсюда вытекает приближенная формула:
Такая связь входного и выходного напряжений дает основание называть рассматриваемую цепь дифференцирующей. Временные рамки, в пределах которых RC-цепъ, характеризуемую определенным значением х, допустимо считать дифференцирующей, можно выявить, изучая реакцию цепи на линейно растущее входное напряжение. Воспользовавшись интегралом Дюамеля, найдем выражение для выходного напряжения, являющегося реакцией на и = at (a — константа):
График этой функции показан на рис. 3.22. Если время мало по сравнению с постоянной времени цепи (t <к т), получаем: ua(t) * at, то есть входное напряжение без искажений проходит на выход цепи. По мере роста времени начинает выполняться обратное неравенство: t» т. И выходное напряжение становится пропорциональным производной входного: ua(t) «ах. Можно считать, что при малых по сравнению с характерным временем процесса значениях х цепь выполняет операцию дифференцирования. Описываемую здесь цепь используют в электронике в обеих ипостасях. Как дифференцирующая она часто применяется для формирования импульсов, совпадающих во времени с наибольшей скоростью изменения входного напряжения. Так из синусоидального напряжения можно сформировать узкие импульсы, отвечающие моментам перехода синусоиды через нулевые значения. Для этого синусоидальное напряжение усиливают, обрезают его «верхушки», формируя тем самым трапецеидальное напряжение, а затем пропускают через RC-цепь с малым по сравнению с периодом синусоиды значением постоянной времени. Другое применение — в качестве неискажающей, или, как иногда говорят, проходной цепи. В этом применении реализуется разрыв цепи протекания постоянного тока на пути следования сигнала. Через проходную цепь сигнал, представляющий собой изменяющееся во времени напряжение, проходит практически без искажений, а напряжение постоянного уровня отсекается «емкостным разрывом».
|