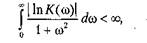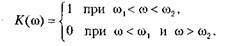ПРИМЕЧАНИЕ. Между временными и частотными характеристиками цепи также существует однозначная связь

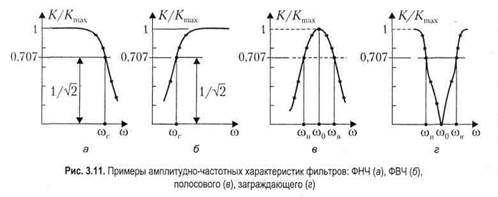
Между временными и частотными характеристиками цепи также существует однозначная связь. Формулы связи вытекают из теории интегральных преобразований Фурье и будут представлены в главе 5.

Анализ пассивных цепей в частотной и временной областях

В этом разделе рассмотрены цепи, которые можно встретить во многих электронных устройствах. Хотя их схемы просты, подходы, используемые здесь для выявления свойств цепей, как и собственно их характеристики, важны для понимания

процессов, протекающих в более сложных устройствах. Некоторые цепи подробно рассмотрены и в частотном, и во временном представлениях. Это позволяет увидеть, каким образом специфика схем проявляется в характеристиках, полученных при одном и другом описании. Важно научиться выявлять параметры одного представления по результатам, известным для другого представления.

Предваряя изложение, уместно заметить, что рассматриваемые в этом разделе схемы в основном составлены из сопротивлений и емкостей. Предпочтение емкостей индуктивностям в фильтрующих схемах отчасти связано с тем, что катушки индуктивности, как элементы, по физической сути своей предполагающие объемность конструкции, трудно «вписываются» в технологический процесс создания интегральных микросхем. Цепи интегральных микросхем формируются на поверхности кристалла и в узком слое вблизи этой поверхности. Создать «объемную» катушку в таких условиях весьма затруднительно, а другие решения, например скручивание проводника в плоскую спираль, поглощают дефицитное пространство, на котором можно было разместить немалое количество интегральных транзисторов. На современной технологической основе в ряде случаев рациональнее достигать эффектов, свойственных катушкам индуктивности, альтернативным способом — посредством транзисторных электронных цепей, содержащих КС-цепи.

Разновидности фильтрующих цепей

Цепи, выделяющие (пропускающие) сигналы определенных частотных диапазонов и подавляющие сигналы на частотах, находящихся за пределами данных диапазонов, называют фильтрами. Существуют фильтры нижних частот (для их именования используют аббревиатуру ФНЧ), фильтры верхних частот (ФВЧ), полосно-пропускающие (ППФ), полоснозаграждающие фильтры (ПЗФ). Последние разновидности называют также полосовыми и заграждающими фильтрами соответственно. (Заграждающие фильтры еще иногда называют режекторными) На рис. 3.11 приведены примеры АЧХ перечисленных цепей. Также стоит вновь взглянуть на рис. 3.2, изображающий АЧХ и ФЧХ фильтра нижних частот, и на рис. 3.3, на котором приведена диаграмма Боде, построенная для этого фильтра.

Область частот, присущих тем колебаниям, что пропускаются фильтром, именуют полосой пропускания (полосой прозрачности). Частоты, характеризующие колебания, которые фильтром подавляются, попадают в полосу подавления (заграждения). Для четкого выделения полосы пропускания используют понятие граничных частот, или частот среза АЧХ. Граничной называют частоту, на которой модуль коэффициента передачи уменьшается в определенной пропорции по отношению к максимальному значению. Обычно за граничную принимают частоту, на которой модуль коэффициента передачи уменьшается в V2 раз или (если при вычислениях пользуются логарифмической шкалой) на 3 дБ. В соответствии с тем, по какую сторону полосы пропускания проходит граничная частота, ее называют верхней или нижней граничной частотой, а также верхней или нижней частотой среза.

При построении цепи, призванной выполнять фильтрующие свойства, стараются сделать полосу пропускания «идеально прозрачной», а в полосе подавления реализовать нулевой коэффициент передачи. Отсюда следует, что АЧХ идеального полосового фильтра должна быть П-образной. Однако вот какой возникает вопрос: а можно ли произвольно задать график АЧХ (частотную функцию модуля коэффициента передачи) или есть ограничения на осуществимость цепей, обладающих заданными частотными характеристиками? Ответом является критерий Палея—Винера [13]. Приводим здесь без доказательства его формулировку: чтобы положительная функция К(&) могла быть модулем коэффициента передачи пассивной электрической цепи, необходимо выполнение условия:

то есть данный интеграл должен сходиться. Функции, не отвечающие критерию Палея—Винера, не могут рассматриваться как модули коэффициента передачи пассивной электрической цепи. В качестве примера выясним, можно ли построить идеальный полосовой фильтр. Его амплитудно-частотная характеристика, как указывалось, должна быть П-образной, то есть иметь вид:

ПРИМЕЧАНИЕ

Критерий Палея—Винера основан на теореме Палея—Винера, относящейся к теории интегральных преобразований Фурье.

Надо заметить, что практически любая цепь, строго говоря, является частотным фильтром. Конечно, коэффициент передачи в схеме обычного делителя на сопротивлениях, показанного рис. 3.12, а, от частоты не зависит. Он равен:

К =UjE=uJe = i?₂/(i?! + R₂) = const(co).

He зависит от частоты и передаточная функция делителя, схема замещения которого содержит комплексные сопротивления Z_l и Z₂, находящиеся в соотношении: Z₂ = Z,y, где у — постоянное число (рис. 3.12, б):

K=UJE = yZJ(Z_i + yZ_t) = Y/(l + y) = const(co).

Однако для реальных цепей всегда можно указать границу на оси частот, за пределами которой цепь начнет подавлять сигнал. Например, в цепи делителя на резисторах по мере увеличения частоты начинают проявляться эффекты, которые учитывают, добавляя в схемы замещения резисторов паразитные элементы. И поэтому АЧХ делителя на резисторах по мере увеличения частоты «заваливается». Но если сигнал таков, что область частот, представляющих практический интерес, расположена в полосе пропускания и, к тому же, на значительном удалении от частоты среза, тогда сигнал подавляться не будет. И в таких случаях рассматриваемые цепи к фильтрам не относят.

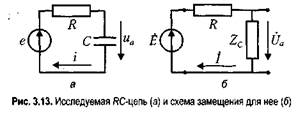
ПРИМЕЧАНИЕ

Появление слова «фильтр» в словесной характеристике цепи косвенно означает, что цепь рассматривают в частотном представлении. Применительно к некоторым цепям можно, однако, услышать фразы из другого словесного ряда. Например, об одних говорят: «интегрирующая цепь», о других: «дифференцирующая цепь». Почему это так, станет ясно из дальнейшего. В основном эти обороты используют при описании свойств цепи во временном представлении.

Частотные свойства простой /?С-цепи

Выясним фильтрующие свойства цепи, схема которой состоит из сопротивления R и емкости С (рис. 3.13, а). Под выходным напряжением цепи будем понимать напряжение и_а между полюсами емкости. Такая цепь, образованная резистором и конденсатором, встречается во многих устройствах. Но схемой, представленной на рис. 3.13, а, можно также моделировать реакцию входных полюсов какой-либо аппаратуры. В частности, входную проводимость измерительных приборов (вольтметров, осциллографов) стремятся делать исчезающе малой. Однако межэлектродная емкость проводников и входная емкость первого блока приборов как некие паразитные элементы всегда в реальности присутствуют. На очень высоких частотах их влияние неизбежно начнет проявляться. Каким образом? Ответ на этот вопрос можно получить, анализируя характеристики схемы, показанной на рис. 3.13, а.

Для изучения фильтрующих свойств цепи надлежит рассматривать ее характеристики в частотном представлении, и, следовательно, в качестве тестового сигнала нужно использовать гармоническое напряжение источника ЭДС: e{t) = £cos(co£). Частоте источника можно задавать любые значения.

Поскольку цепь линейная, воспользуемся методом комплексных амплитуд. Сопоставим всем гармоническим колебаниям комплексные амплитуды. В частности, для ЭДС имеем: Ё = Е. Перейдем далее к рассмотрению схемы замещения (рис. 3.13, б), которая структурно представляет собой делитель на сопротивлениях. Коэффици­ент передачи (передаточная функция) этой цепи находится по формуле:

K=U_a/E = Z_c/(R + Z_c) = 1/(1 + J<*RC).

Модуль коэффициента передачи К и его аргумент а имеют вид:

Отсюда видно, что при со -> 0 выходное напряжение не ослабляется (К «1) и не сдвигается по фазе (а «0). Зато при со -» оо получаем: К(<х>) * l/(a>RC), а -> - л/2.

Это означает, что по мере увеличения частоты К(оз) -» 0. Таким образом, данная цепь пропускает без ослабления колебания малых (низких) частот и подавляет колебания высоких частот. Следовательно, цепь является фильтром нижних частот. Границу (частоту среза со_с), разделяющую полосы пропускания и подавления, найдем на основании формулы:

К(ю_с) = Я_тах/л/2=1Л/2* 0,707.

Из нее вытекает: со_с = \/{RC). Заметим, что на этой частоте a = arctg(-l) = = -л/4, и значит, фазовый сдвиг выходного напряжения по отношению к входному на частоте среза со_с составляет -я/4.

Перепишем полученные ранее выражения, введя в них со_с:

Теперь можно построить АЧХ — график функции К(ю), и ФЧХ — график функции сх(со). Отметим характер асимптотического поведения АЧХ и ФЧХ в полосе прозрачности (при со/©,. «1) и в полосе подавления (при со/со,.» 1):

К «О, а ~ О при со/ со₍. <зс 1;

K^-j(i)_c/a, К ж со_с/со, а ж -л/2 при со/ со_с» 1.

Видно, что в полосе подавления модуль коэффициента передачи уменьшается обратно пропорционально частоте. На рис. 3.14 построены диаграмма Боде (сверху) и ФЧХ данной цепи (снизу).

Отметим, что в полосе пропускания асимптота коэффициента передачи проходит по оси абсцисс, а в полосе подавления асимптотой является прямая с наклоном, составляющим 20 дБ на декаду (декада — десятикратное изменение значения) или 6 дБ на октаву (октава — изменение значения вдвое). Пересекаются асимптоты на частоте среза, на которой К_д = -3 дБ. Уместно заметить, что наклон в 20 дБ на декаду характерен для простейших частотных фильтров — фильтров первого рода. Чтобы увеличить наклон графика Боде в полосе подавления, приходится усложнять схему, добавляя элементы, обладающие реактивным сопротивлением, — емкости, индуктивности.