Базис и размерность ЛП, разложение вектора по векторам базиса
В линейном пространстве можно найти такую систему векторов, через которую можно единственным образом выразить любой вектор этого пространства. Она называется базисом линейного пространства. Определение 1.9. Базисом 1) система векторов 2) система векторов Рассмотрим простейшие свойства базиса. Теорема 1.1. Если
□ Предположим, что вектор
Вычитая из первого равенства второе, получим
Так как система векторов Определение 1.10. Коэффициенты Координаты
(нижний индекс у вектор-столбца означает привязку координат к базису Разложение (1.9) удобно записывать в условном матричном виде
Отметим, что базис – это упорядоченная система векторов. Если поменять местами два разных вектора в базисе Базис линейного пространства определяется неоднозначно. Если Теорема 1.2. При сложении любых двух векторов в линейном пространстве их координаты в одном и том же базисе складываются, а при умножении вектора на число его координаты умножаются на это число. □ Действительно, пусть два вектора
где
то есть вектору Следующая теорема является непосредственным следствием определения базиса линейного пространства. Теорема 1.3. Базис является минимальной порождающей системой векторов. Базис является максимальной линейно независимой системой векторов. Первое утверждение теоремы означает, что базис порождает линейное пространство, и любая система векторов, являющаяся частью базиса, не является порождающей это пространство. Если из базиса удалить хотя бы один вектор, то полученная система не будет являться порождающей пространство. Второе утверждение означает, что если дополнить базис любым вектором этого пространства, то полученная система (которая будет являться линейно зависимой), не является базисом пространства. Определение 1.11. Размерностью Если Отметим также следующие очевидные свойства базиса линейного пространства. 1) Если 2) Пусть
|

 в линейном пространстве
в линейном пространстве 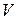 называется упорядоченная система векторов
называется упорядоченная система векторов 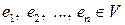 , удовлетворяющая условиям:
, удовлетворяющая условиям: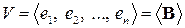 .
.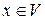 может быть единственным образом разложен по векторам базиса
может быть единственным образом разложен по векторам базиса 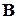 , то есть существуют и однозначно определены числа
, то есть существуют и однозначно определены числа 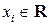
 такие, что:
такие, что: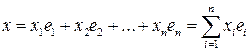 . (1.9)
. (1.9)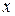 в базисе
в базисе 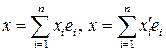 .
. .
.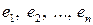 является линейно независимой, то последнее равенство возможно только в том случае, когда все коэффициенты
является линейно независимой, то последнее равенство возможно только в том случае, когда все коэффициенты 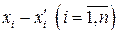 линейной комбинации в левой части равны нулю, то есть
линейной комбинации в левой части равны нулю, то есть 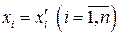 , что и доказывает единственность разложения (1.9) для вектора
, что и доказывает единственность разложения (1.9) для вектора 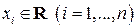 в разложении (1.9) называются координатами вектора
в разложении (1.9) называются координатами вектора 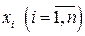 вектора
вектора  или
или 
 . (1.10)
. (1.10)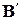 . Порядок векторов в базисе фиксируют для того, чтобы задать определенный порядок коэффициентов разложения произвольного вектора. Это позволяет заменить линейную комбинацию, представляющую вектор, упорядоченным набором ее коэффициентов и тем самым упростить запись. Порядок векторов в базисе определяется их нумерацией.
. Порядок векторов в базисе фиксируют для того, чтобы задать определенный порядок коэффициентов разложения произвольного вектора. Это позволяет заменить линейную комбинацию, представляющую вектор, упорядоченным набором ее коэффициентов и тем самым упростить запись. Порядок векторов в базисе определяется их нумерацией.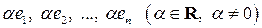 также образуют базис этого же линейного пространства.
также образуют базис этого же линейного пространства.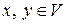 в базисе
в базисе 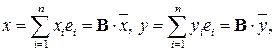
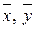 – координатные вектор-столбцы векторов
– координатные вектор-столбцы векторов  . Тогда
. Тогда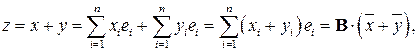
 в базисе
в базисе 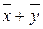 . ■
. ■ пространства
пространства 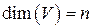 . При этом
. При этом 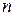 - мерным (конечномерным) линейным пространством.
- мерным (конечномерным) линейным пространством.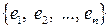 – линейно независимая система векторов пространства
– линейно независимая система векторов пространства  – некоторая система векторов, причем
– некоторая система векторов, причем 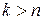 . Тогда система векторов
. Тогда система векторов 


