ЛЕКЦИИ ПО ДИСЦИПЛИНЕ
«ЛИНЕЙНАЯ АЛГЕБРА»
Направление 080100
«Экономика»
Очная форма обучения
Рязань 2012
Тема 7. Линейные (векторные) пространства
1. Линейные пространства: определение (аксиомы).
Примеры линейных пространств.
Линейная зависимость, независимость системы векторов в ЛП.
Основные теоремы (свойства).
Базис и размерность ЛП, разложение вектора по векторам базиса.
Примеры базисов. Базис и размерность ЛП решений ОСЛАУ.
Переход от базиса к базису, свойства матрицы перехода.
Понятие линейного пространства
Центральное место среди всех понятий линейной алгебры занимает понятие линейного пространства.
Определение 1.1. Непустое множество  элементов (векторов)
элементов (векторов) 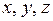 , …,над которыми определены операции сложения двух векторов (при всех
, …,над которыми определены операции сложения двух векторов (при всех  :
: 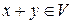 ) и умножения вектора на число (при всех
) и умножения вектора на число (при всех  ,
,  :
:  ) так, что выполняются условия (аксиомы):
) так, что выполняются условия (аксиомы):
 : при всех
: при всех 
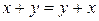 ;
;
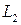 : при всех
: при всех 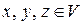
 ;
;
 : существует вектор
: существует вектор  такой, что для каждого
такой, что для каждого 
 ;
;
 : для каждого
: для каждого  существует вектор
существует вектор 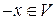 такой, что
такой, что  ;
;
 : для каждого
: для каждого 
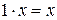 ;
;
 : для каждого
: для каждого  , при всех
, при всех 
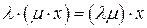 ;
;
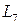 : для каждого
: для каждого  , при всех
, при всех 
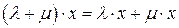 ;
;
 : при всех
: при всех  , для каждого
, для каждого 
 ,
,
называется линейным пространством.
Согласно определению линейного пространства  сумма определена для любых элементов из
сумма определена для любых элементов из  и всегда является элементом множества
и всегда является элементом множества  . При этом говорят, что множество
. При этом говорят, что множество  замкнуто относительно операции сложения. Аналогично, согласно тому же определению, множество
замкнуто относительно операции сложения. Аналогично, согласно тому же определению, множество  замкнуто относительно операции умножения его элементов на действительные числа.
замкнуто относительно операции умножения его элементов на действительные числа.
Прокомментируем аксиомы линейного пространства. Условия  ,
, 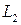 называются соответственно аксиомами коммутативности и ассоциативности относительно сложения векторов. Условие
называются соответственно аксиомами коммутативности и ассоциативности относительно сложения векторов. Условие  есть аксиома существования нулевого вектора в пространстве. Условие
есть аксиома существования нулевого вектора в пространстве. Условие  есть аксиома существования противоположного вектора для каждого вектора пространства. Условие
есть аксиома существования противоположного вектора для каждого вектора пространства. Условие  означает, что число 1 есть нейтральный элемент относительно умножения его на вектор пространства. Условие
означает, что число 1 есть нейтральный элемент относительно умножения его на вектор пространства. Условие  означает ассоциативность умножения на число. Условия
означает ассоциативность умножения на число. Условия 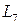 и
и  означают, что умножение на число и сложение связаны законом дистрибутивности по числам и векторам соответственно.
означают, что умножение на число и сложение связаны законом дистрибутивности по числам и векторам соответственно.
В определении линейного пространства важно не только то, из каких элементов состоит базовое множество  , но и как введены операции над элементами этого множества. Одно и то же множество при одних операциях может быть линейным пространством, а при других – нет.
, но и как введены операции над элементами этого множества. Одно и то же множество при одних операциях может быть линейным пространством, а при других – нет.
Сформулируем простейшие свойства линейного пространства, непосредственно следующие из аксиом линейного пространства.
1) Линейное пространство имеет только один нулевой вектор  .
.
2) Каждый вектор линейного пространства имеет только один единственный противоположный. Противоположным к нулевому вектору является сам нулевой вектор.
3) Если 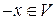 есть противоположный к элементу
есть противоположный к элементу  линейного пространства, то вектор
линейного пространства, то вектор 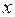 является противоположным к вектору
является противоположным к вектору  , то есть
, то есть
 .
.
4) Произведение произвольного элемента  линейного пространства на число 0 равно нулевому вектору:
линейного пространства на число 0 равно нулевому вектору:
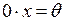
5) Вектор 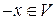 , противоположный данному вектору
, противоположный данному вектору  , равен произведению вектора
, равен произведению вектора 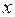 на число
на число 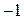 :
:
 .
.

 элементов (векторов)
элементов (векторов) 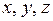 , …,над которыми определены операции сложения двух векторов (при всех
, …,над которыми определены операции сложения двух векторов (при всех  :
: 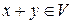 ) и умножения вектора на число (при всех
) и умножения вектора на число (при всех  ,
,  :
:  ) так, что выполняются условия (аксиомы):
) так, что выполняются условия (аксиомы): : при всех
: при всех 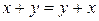 ;
;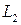 : при всех
: при всех 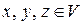
 ;
; : существует вектор
: существует вектор  такой, что для каждого
такой, что для каждого  ;
; : для каждого
: для каждого 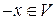 такой, что
такой, что  ;
; : для каждого
: для каждого 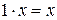 ;
; : для каждого
: для каждого 
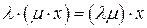 ;
;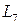 : для каждого
: для каждого 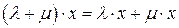 ;
; : при всех
: при всех  ,
,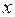 является противоположным к вектору
является противоположным к вектору  , то есть
, то есть .
.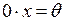
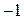 :
: .
.


