- При a = b = 0 параллельный перенос совпадает с тождественным преобразованием. При этом каждая точка плоскости – неподвижная точка преобразования;
- При a 2 + b 2 > 0 параллельный перенос не имеет неподвижных точек.
 Теорема 12.7.
Теорема 12.7.
Каковы бы ни были две точки A и  существует один и только один параллельный перенос, при котором точка A переходит в точку
существует один и только один параллельный перенос, при котором точка A переходит в точку 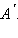
Доказательство
 Теорема 12.8.
Теорема 12.8.
Параллельный перенос есть движение.
Доказательство
Действительно, две произвольные точки 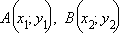 переходят при параллельном переносе в точки переходят при параллельном переносе в точки  Поэтому Поэтому 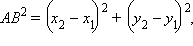  Отсюда Отсюда 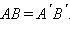 Таким образом, параллельный перенос сохраняет расстояние, а значит, является движением. Теорема доказана. Таким образом, параллельный перенос сохраняет расстояние, а значит, является движением. Теорема доказана.
|
 Теорема 12.9.
Теорема 12.9.
Движение, сохраняющее направление, является параллельным переносом.
Доказательство
Пусть f – движение, переводящее точку A в точку 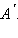 Пусть Пусть 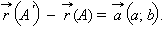 Выберем произвольную отличную от A точку B, и пусть Выберем произвольную отличную от A точку B, и пусть 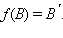 По условию По условию  По теореме 12.8 имеем По теореме 12.8 имеем 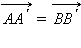 или, следовательно, или, следовательно, 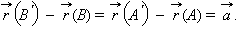 Отсюда Отсюда  Ввиду произвольности выбора точки B теорема доказана. Ввиду произвольности выбора точки B теорема доказана.
|
| Свойства параллельного переноса в пространстве
| факт
|
Параллельный перенос есть движение.
При параллельном переносе прямая переходит либо в себя, либо в параллельную ей прямую.
При параллельном переносе плоскость переходит либо в себя, либо в параллельную ей плоскость.
Параллельный перенос задается парой соответствующих точек, т.е. каковы бы ни были точки 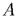 и
и 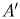 , существует единственный параллельный перенос, при котором точка
, существует единственный параллельный перенос, при котором точка 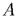 переходит в точку
переходит в точку 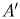 .
.
Редактор [Редактор]

 Теорема 12.7.
Теорема 12.7. существует один и только один параллельный перенос, при котором точка A переходит в точку
существует один и только один параллельный перенос, при котором точка A переходит в точку 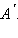
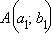 и
и 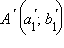 – заданные точки. Определим параллельный перенос f равенствами
– заданные точки. Определим параллельный перенос f равенствами 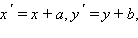 где
где 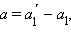
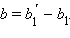 Тогда данный параллельный перенос действительно переводит точку A в
Тогда данный параллельный перенос действительно переводит точку A в 

 По определению φ:
По определению φ:
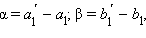 т. е.
т. е. 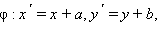 что совпадает с f, а это противоречит предположению. Теорема доказана.
что совпадает с f, а это противоречит предположению. Теорема доказана.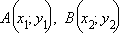 переходят при параллельном переносе в точки
переходят при параллельном переносе в точки  Поэтому
Поэтому 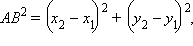
 Отсюда
Отсюда 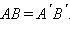 Таким образом, параллельный перенос сохраняет расстояние, а значит, является движением. Теорема доказана.
Таким образом, параллельный перенос сохраняет расстояние, а значит, является движением. Теорема доказана.
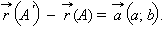 Выберем произвольную отличную от A точку B, и пусть
Выберем произвольную отличную от A точку B, и пусть 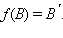 По условию
По условию  По теореме 12.8 имеем
По теореме 12.8 имеем 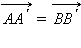 или, следовательно,
или, следовательно, 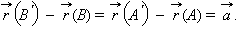 Отсюда
Отсюда  Ввиду произвольности выбора точки B теорема доказана.
Ввиду произвольности выбора точки B теорема доказана.
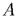 и
и 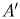 , существует единственный параллельный перенос, при котором точка
, существует единственный параллельный перенос, при котором точка 


