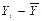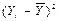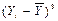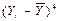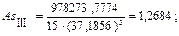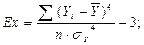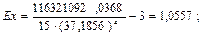Особенности оценки параметров нелинейных моделей
Соотношение между социально-экономическими явлениями и процессами далеко не всегда можно выразить линейными функциями. Так, нелинейными оказываются производственные функции (зависимости между объемом произведенной продукции и основными факторами производства – трудом, капиталом и т. д.), функции спроса (зависимость между спросом на товары, услуги и их ценами или доходом) и др. Если между экономическими явлениями существуют нелинейные соотношения, то они выражаются с помощью соответствующих нелинейных функций. Нелинейность может проявляться как относительно переменных, так и относительно входящих в функцию коэффициентов (параметров). Различают два класса нелинейных регрессий
Для оценки параметров нелинейных моделей используются два подхода. Первый подход основан на линеаризации модели и заключается в том, что с помощью подходящих преобразований исходных переменных исследуемую зависимость представляют в виде линейного соотношения между преобразованными переменными. Второй подход обычно применяют в случаях, когда подобрать соответствующее линеаризующее преобразование не удается. Тогда использует методы нелинейной оптимизации на основе исходных переменных. Применяемые чаще всего в экономическом анализе виды нелинейных регрессий следующие: полином второго порядка, гипербола, степенная функция и показательная функция. Однако параметров нелинейной регрессии по переменным, включенным в анализ, но линейным по оцениваемым параметрам, проводиться с помощью МНК путем решения нормальных уравнений. Регрессии, нелинейные по переменным, но линейные по оцениваемым параметрам: 1. полином второго порядка ŷx = a0 + a1xi + a2xi2 (3.25) Нормальные уравнения:
2. гипербола ŷx = a0 + a1 Нормальные уравнения
Или заменим 1/ xi на новую переменную X. В результате получим линейное уравнение: Ŷx = a0 +a1X. (3.29) Параметры определяются из следующих формул:
Линеаризация регрессий, нелинейных по оцениваемым параметрам: 1. степенная функция ŷx Для определения параметров степенной функции с помощью МНК необходимо привести ее к линейному виду путем логарифмирования обеих частей уравнения:
Это уравнение представляет собой прямую линию на графике, по осям которого откладываются не сами числа, а их логарифмы (так называемая логарифмическая школа или логарифмическая сетка). Пусть Y=ln ŷx, X=ln xi, A=ln a0. Тогда уравнение примет вид Y = A + a1X (3.33) Параметры модели определяются по следующим формулам:
2. показательная функция ŷx Линеаризацию переменных проведем путем логарифмирования обеих частей уравнения: ln ŷx = Уравнение изображается прямой линией на полулогарифмической сетке, которая получается как сочетание натуральной шкалы для значения независимой переменной х и логарифмической шкалы – для значения зависимой переменной у. Пусть Y = ln ŷx, A = ln a0, B =ln a1. Тогда уравнение примет вид
Параметры модели определяются по следующим формулам:
При использовании любой формы криволинейной корреляционной зависимости теснота связи между переменными может быть измерена с помощью индекса корреляции, который определяется аналогично коэффициенту корреляции для линейной формы связи. Уравнение корреляционной связи должно быть по возможности более простым, чтобы сущность изучаемой зависимости между переменными проявлялась достаточно четко, а параметры уравнения поддавались определенному экономическому толкованию. Вопрос выбора соответствующего уравнения связи решается в каждом случае отдельно. 3. Методика построения модели парной регрессии По пятнадцати сельскохозяйственным предприятиям Орловской области за 200х г. известны значения двух признаков: Таблица 3.1. – Исходные данные для анализа
Требуется: 1. Вычислить описательные статистики. Проверить характер распределения признаков. При необходимости удалить аномальные наблюдения. 2. Построить поле корреляции. Выдвинуть гипотезу о форме связи признаков. 3. Для характеристики зависимости у от х: а) построить линейное уравнение парной регрессии у от х; б) дать экономическую интерпретацию уравнению регрессии исчислив средний коэффициент эластичности в) оценить полученную модель через среднюю ошибку аппроксимации и F-критерий Фишера и сделать вывод; г) провести статистическую оценку значимости коэффициентов регрессии и корреляции (с помощью t-статистики Стьюдента и путем расчета доверительного интервала каждого из показателей). 4) Рассчитать параметры регрессии, построенной по уравнению равносторонней гиперболы. Оценить полученную модель через среднюю ошибку аппроксимации и F-критерий Фишера, сделать вывод. 5) Рассчитать параметры степенной регрессионной модели. Оценить полученную модель через среднюю ошибку аппроксимации и F-критерий Фишера, сделать вывод. 6). Обосновано выбрать лучшую модель и рассчитать по ней прогнозное значение результата, если прогнозное значение фактора увеличится на 25% от среднего уровня. Определить доверительный интервал прогноза при уровне значимости α = 0,05. Порядок выполнения: Для нашего примера: Y – Валовой доход отрасли растениеводства, приходящийся на 100 га пашни (тыс. руб.) (результативный признак); Х – Затраты труда в растениеводстве на 100 га пашни, тыс. чел.-час./га (факторный признак). Прежде чем приступить непосредственно к анализу, необходимо проверить выполнение трех основных условий применения корреляционно-регрессионного анализа. 1) 1.1.Проверим, насколько для данной совокупности действует Закон больших чисел. В данном случае рекомендуется отобрать из генеральной совокупности с помощью случайной бесповторной выборки как минимум 10 объектов для исследования (число наблюдений должно хотя бы в 10 раз превышать количество факторных признаков в модели). Данное правило соблюдено. Зависимость изучается по данным 15 предприятий. 1.2. Проверим характер распределения. Для этого рассчитаем среднее квадратическое отклонение (σ) и коэффициент вариации (v) для каждого из показателей по формулам:
По исходным данным рассчитаем X2, Y2, ΣX2, ΣY2(таблица 3.2) Рассчитаем среднее квадратическое отклонение для каждого из признаков: Таблица 3.2. - Расчетные величины, необходимые для определения среднего квадратического отклонения и коэффициента вариации
Рассчитаем среднее квадратическое отклонение по получившимся данным для каждого из признаков
Рассчитаем коэффициент вариации для каждого из признаков:
Поскольку коэффициенты вариации по каждому из признаков не превышают значения 0,35, то может сделать вывод об однородности изучаемой совокупности. 1.3. Для применения метода наименьших квадратов при нахождении параметров уравнения регрессии необходимо, чтобы распределение по результативному признаку подчинялось нормальному закону. Проверить распределение на нормальность можно путем расчета показателей асимметрии первого, второго и третьего порядков и показатель эксцесса. При нормальном распределении вариационный укладывается в границы
Rу =211,15-64,82 = 146,33 ц/га; Rу < 223,14. Mo=111,03 тыс. руб.; Me=111,03 тыс. руб.; Рассчитаем асимметрию первого порядка:
Таблица 3.3. – Расчетные величины
Асимметрия второго порядка рассчитывается по формулам:
Рассчитаем асимметрию третьего порядка:
Найдем значение эксцесса:
Полученные данные позволяют сделать следующий вывод. Значения асимметрии первого, второго, третьего порядков и эксцесса достаточно малы, мода, медиана и среднее значение результативного признака приближенно равны, следовательно, совокупность подчиняется нормальному закону и для нахождения параметров уравнения регрессии применим Метод наименьших квадратов (МНК).
|



 ;
; ; (3.26)
; (3.26)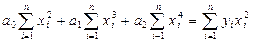 .
.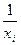 (3.27)
(3.27)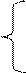
 ;
; . (3.28)
. (3.28)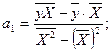 a0 =
a0 = 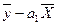 (3.30)
(3.30)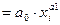 (3.31)
(3.31) ln ŷx
ln ŷx 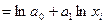 (3.32)
(3.32)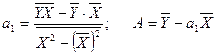 (3.34)
(3.34) (3.35)
(3.35) (3.36)
(3.36) (3.37)
(3.37) (3.38)
(3.38)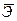 , парный линейный коэффициент корреляции – r, коэффициент детерминации – D;
, парный линейный коэффициент корреляции – r, коэффициент детерминации – D;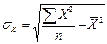 (1)
(1) (2)
(2)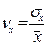
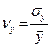 (3)
(3)




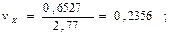
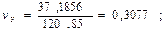
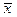 ± 3σ; размах вариации R = 6σ. Это означает, что при нормальном распределении вероятность попадания единичного наблюдения в интервал ± 3σ равна 0,997. Величину 3σ считают максимально допустимой ошибкой и отбрасывают результаты экспериментов, для которых величина отклонения от среднего превышает это значение («правило 3 сигм»).
± 3σ; размах вариации R = 6σ. Это означает, что при нормальном распределении вероятность попадания единичного наблюдения в интервал ± 3σ равна 0,997. Величину 3σ считают максимально допустимой ошибкой и отбрасывают результаты экспериментов, для которых величина отклонения от среднего превышает это значение («правило 3 сигм»).