Степенная модель.
Уравнение степенной модели имеет вид:
Данная функция нелинейна относительно параметров, но линейна по переменным. Прежде, чем проводить анализ необходимо перейти от нелинейной формы к линейной. В регрессиях нелинейных относительно параметров процедура линеаризации (аноморфоза) производится путем логарифмирования обеих частей уравнения:
Введем замену: Вновь полученное уравнение будет иметь вид: Найдем среднее квадратическое отклонение по L:
Таблица 3.7. – Расчетные величины, необходимые для определения параметров уравнения
Для расчета параметров уравнения регрессии воспользуемся готовыми формулами:
Уравнение принимает вид: Проведем потенцирование полученного уравнения:
Коэффициент эластичности рассчитывается по формуле:
С увеличением затрат труда в растениеводстве на 1 % от своего среднего значения валовой доход отрасли увеличивается в среднем на 0,56 %.
Рисунок 3.3. – Влияние затрат труда в растениеводстве на валовой доход отрасли (степенная модель) Для расчета индекса корреляции выполним вспомогательные расчеты (таблица 3.8).
Индекс корреляции показывает, что связь между затратами труда в растениеводстве и валовым доходом отрасли заметная. По индексу корреляции нельзя судить о направлении связи. Коэффициент детерминации рассчитаем по формуле:
Таблица 3.8. – Расчетные величины, необходимые для расчета индекса корреляции и определения показателей аппроксимации
Следовательно, вариация валового дохода отрасли растениеводства на 30% объясняется вариацией затрат труда в растениеводстве, а остальные 70% вариации валового дохода отрасли обусловлены изменением других, не учтенных в модели факторов. Средняя ошибка аппроксимации равна 18,7%. т.е. в среднем расчетные значения валового дохода отрасли растениеводства, приходящийся на 100 га пашни, отличаются от фактических на 18,7%, что не входит в допустимый предел. Данная модель имеет наименьшую ошибку аппроксимации. Оценим модель через F-критерий Фишера. Выдвинем H0 о статистической незначимости полученного уравнения регрессии и показателя тесноты связи.
Сравним фактическое значение F-критерия с табличным. Для этого выпишем из таблицы «Значения F-Фишера при уровне значимости α=0,05» табличное значение. Так как Fфакт>Fтабл,то при заданном уровне вероятности α=0,05 следует отвергнуть нулевую гипотезу о статистической незначимости уравнения регрессии и показателя тесноты связи. Полученные оценки позволяют использовать данное уравнение для прогноза. 8. Выберем наиболее подходящую для прогнозирования модель. Линейная модель имеет наибольшее значение коэффициента детерминации. Кроме того, данная модель значима по F-критерию Фишера. Выполним прогнозирование размера величины валового дохода отрасли растениеводства по уравнению прямой линии. Найдем прогнозное значение факторного признака, составляющего 125% от его среднего уровня:
Выполним прогноз значения результативного признака (точечный прогноз):
Оценим точность прогноза. Рассчитаем случайную ошибку прогноза:
Предельная ошибка прогноза, которая в 95% случаев не будет превышена, рассчитывается следующим образом:
С вероятностью 95% можно утверждать, что прогнозируемое значение результативного признаканаходится в пределах: 22,8786< Yp <266,2452 Выполненный прогноз Валового дохода оказался надежным (p = 1-α = 1-0,005 = 0,95), но неточным, так как диапазон верхней и нижней границ доверительного интервала составляет 11,6 раза: Вопросы для самоконтроля: 1. Раскройте методику вычисления параметров парного линейного уравнения регрессии. 2. Поясните смысл коэффициента регрессии, назовите способы его оценивания, покажите, как он используется для расчета мультипликатора в функции потребления. 3. Что такое число степеней свободы и как оно определяется для факторной и остаточной сумм квадратов? 4. Какова концепция F-критерия Фишера? 5. Как оценивается значимость параметров уравнения регрессии? 6. В чем отличие стандартной ошибки положения линии регрессии от средней ошибки прогнозируемого индивидуального значения результативного признака при заданном значении фактора? 7. Какой нелинейной функцией может быть заменена парабола второй степени, если не наблюдается смена направленности связи признаков? 8. Запишите все виды моделей, нелинейных относительно: 9. В чем отличие применения МНК к моделям, нелинейным относительно включаемых переменных и оцениваемых параметров? 10. Как определяются коэффициенты эластичности по разным видам регрессионных моделей? 11. Назовите показатели корреляции, используемые при нелинейных соотношениях рассматриваемых признаков. 12. Перечислите особенности сельскохозяйственного производства, его анализа и моделирования. 13. Назовите основные типы нелинейных регрессионных моделей, применяемые в сельскохозяйственном производстве. 14. Возможность применение регрессионных моделей в прогнозировании и в анализе хозяйственной деятельности
|



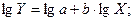
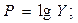


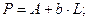

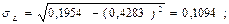










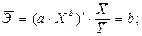



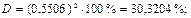




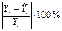

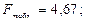
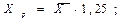




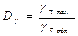 = 233.35/162.15=11,6.
= 233.35/162.15=11,6.


