Парная регрессия и корреляция в эконометрических исследованиях
ТЕМА 3. ОДНОФАКТОРНЫЕ КОРРЕЛЯЦИОННО - РЕГРЕССИОННЫЕ МОДЕЛИ И ВОЗМОЖНОСТИ ИХ ПРИМЕНЕНИЯ ДЛЯ АНАЛИЗА И ПРОГНОЗА Парная регрессия и корреляция в эконометрических исследованиях Особенности оценки параметров нелинейных моделей 3. Методика построения модели парной регрессии Литература: 1, 2, 3, 4, 5,11, 16, 20, 22, 23,24,25, 29. Парная регрессия и корреляция в эконометрических исследованиях Простая (парная) регрессия представляет собой регрессию между двумя переменными – у и х, т.е. модель вида y = f(x), (3.1) где у – зависимая переменная (результативный признак); х – независимая, или объясняющая, переменная (признак-фактор). Различают линейные и нелинейные регрессии. Линейная регрессия: y = a+b*x+e. Нелинейные регрессии делятся на два класса: регрессии, нелинейные относительно включенных в анализ объясняющих переменных, но линейные по оцениваемым параметрам: · полиномы разных степеней y = a+b1x+b2x2+b3x3+ e · равносторонняя гипербола y = a+b/x+ e · степенная y = axb * e · показательная y = a bx e · экспоненциальная y = e a+b*x * e Простейшей системой связи является линейная связь между двумя признаками – парная линейная регрессия. Уравнение парной линейной корреляционной связи называется уравнением парной регрессии и имеет вид: Ŷ = a+bx, (3.2) где ŷ – среднее значение результативного признака у при определенном значении факторного признака х; а – свободный член уравнения; b – коэффициент регрессии, измеряющий среднее отношение отклонения результативного признака от его средней величины к отклонению факторного признака от его средней величины на одну единицу его измерения – вариация у, приходящаяся на единицу вариации х. Построение уравнения регрессии сводится к оценке ее параметров. Для оценки параметров регрессий, линейных по параметрам, используют Метод наименьших квадратов (МНК) МНК позволяет получить такие оценки параметров, при которых сумма квадратов отклонений фактических значений результативного признака у от теоретических ŷ минимальна, т.е.
na + bå x = å y aå x + bå x2 = å xy (3.3) Можно решить эту систему уравнений по исходным данным или использовать формулы, вытекающие из этой системы: a = b= Тесноту связи изучаемых явлений оценивает линейный коэффициент парной корреляции rxy= Знак коэффициента корреляции показывает направление связи: «+» – связь прямая, «–» – связь обратная. Абсолютная величина характеризует степень тесноты связи. В соответствии со шкалой Чеддока:
Если r= 0, то связь между факторами х и у отсутствует.
Индекс корреляции ρ;xy характеризует силу связи в нелинейной регрессии. (0 ρxy= Средний коэффициент эластичности
Для линейной регрессии
Задача дисперсионного анализа состоит в анализе дисперсии зависимой переменной: Правило сложения дисперсий: å(yi - где å(yi - å(ŷx - å(yi - ŷx)2 – остаточная сумма квадратов отклонений.
Долю дисперсии, объясняемую регрессией, в общей дисперсии результативного признака y характеризует коэффициент (индекс) детерминации R2;
Для практического использования корреляционно-регрессионных моделей большое значение имеет их адекватность, т.е. соответствие фактическим статистическим данным. Корреляционно-регрессионный анализ проводится обычно по ограниченному объему статистической совокупности. Поэтому показатели регрессии и корреляции – параметры уравнения регрессии, коэффициенты корреляции и детерминации могут быть искажены действием случайных факторов. Чтобы проверить насколько эти показатели характерны для генеральной совокупности, не являются ли они результатом действия случайных величин, необходимо проверить адекватность построенных статистических моделей. Необходимо оценить модель через среднюю ошибку аппроксимации и F-критерий Фишера. Средняя ошибка аппроксимации – среднее отклонение расчетных значений от фактических:
Допустимый предел значений F-тест – оценивание качества уравнения регрессии – состоит в проверке гипотезы Но о статистической незначимости уравнения регрессии и показателя тесноты связи. Для этого выполняется сравнение фактического F факт и критического (табличного) F табл значений F-критерия Фишера. Любая сумма квадратов отклонений связана с числом степеней свободы, которое зависит от числа единиц совокупности n и числом определяемых по ней констант (переменных при х)(m). Dобщ= å(yi - Dфакт= å(ŷx - Dост= å(yi - ŷx)2 /n-m-1 Определение дисперсии на одну степень свободы приводит дисперсии к сравнимому виду. Сопоставляя факторную и остаточную дисперсии в расчете на одну степень свободы, получим величину F-критерия:
F = Dфакт/Dост = где F-критерий для проверки нулевой гипотезы Но: Dфакт = Dост. Табличное значение F-критерия – это максимальная величина отношения дисперсий, которая может иметь место при случайном их расхождении для данного уровня вероятности (a) наличия нулевой гипотезы (уровень значимости a - вероятность отвергнуть правильную гипотезу при условии, что она верна). Вычисленное значение F-отношения признается достоверным (отличным от единицы), если оно больше табличного. В этом случае нулевая гипотеза об отсутствии связи признаков отклоняется и делается вывод о существенности этой связи: Fфакт > Fтабл – Но отклоняется. Если эта величина окажется меньше табличного, то вероятность нулевой гипотезы выше заданного уровня (например, 0, 05) и она не может быть отклонена без серьезного риска сделать неправильный вывод о наличии связи. В этом случае уравнение регрессии считается статистически незначимым. Но не отклоняется. Для нахождения Fтабл. необходимо определить следующие величины: 1)
2) k1=m (число степеней свободы факторной дисперсии); 3)k2=n-m-1 (число степеней свободы остаточной дисперсии); где m – число параметров при переменных х. n – число единиц совокупности. Замечание: Fфактич. должен быть обязательно больше 1, в противном случае необходимо рассматривать F-1. При этом k1= n - m - 1 и k2 = m = 1.
Для оценки статистической значимости коэффициентов регрессии и корреляции рассчитываются t-критерий Стьюдента и доверительные интервалы каждого из показателей, т.е. о незначимом их отличии от нуля. Оценка значимости коэффициентов регрессии и корреляции с помощью t-критерия Стьюдента проводится путем сопоставления их значений с величиной ошибки:
Случайные ошибки параметров линейной регрессии и коэффициента корреляции определяются по формулам:
где S2 ост – остаточная дисперсия на одну степень свободы.
Сравнивая фактическое и критическое (табличное) значения t-статистики принимаем или отвергаем гипотезу Но. Если t табл < t факт , то Но отклоняется, т.е. a, b, r не случайно отличаются от нуля и сформировались под влиянием систематически действующего фактора x. Если t табл > t факт , то гипотеза Но не отклоняется и признается случайная природа формирования a, b, r. Для расчета доверительного интервала определяем предельную ошибку ∆ для каждого показателя: ∆a = tтабл ma, ∆b = tтабл mb (3.19) Доверительные интервалы рассчитываются следующим образом:
Если в границы доверительного интервала попадает ноль, т.е. нижняя граница отрицательна, а верхняя положительна, то оцениваемый параметр принимается нулевым, так как он не может одновременно принимать и положительное, и отрицательное значение. Прогнозное значение результативного признака yp определяется путем подстановки в уравнение регрессии соответствующего прогнозного значения xp. Вычисляется средняя стандартная ошибка прогноза
где Далее строится доверительный интервал прогноза:
где
|

 å(y – ŷ)2 min
å(y – ŷ)2 min Система нормальных уравнений:
Система нормальных уравнений: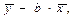 (3.4)
(3.4) ,или
,или 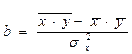 (3.5)
(3.5) rxy (для линейной регрессии)
rxy (для линейной регрессии) 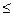 rxy
rxy 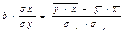 , (3.6)
, (3.6)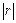
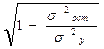 =
=  . (3.7)
. (3.7)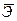 показывает, на сколько процентов в среднем по совокупности изменится результат y от своей средней величины при изменении фактора x на 1% от своего среднего значения:
показывает, на сколько процентов в среднем по совокупности изменится результат y от своей средней величины при изменении фактора x на 1% от своего среднего значения: . (3.8)
. (3.8)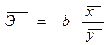 (3.9)
(3.9)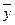 )2 = å(ŷx -
)2 = å(ŷx - 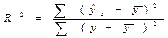 . (3.11)
. (3.11) =
= 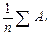 (3.12)
(3.12)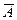 - не более 8 – 10%.
- не более 8 – 10%.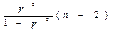 (3.14)
(3.14)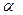 - уровень вероятности отвергнуть верную гипотезу;
- уровень вероятности отвергнуть верную гипотезу; = 0,05; 0,01; 0,1 (можно брать любое из предложенных значений, но оговаривая "с вероятностью…").
= 0,05; 0,01; 0,1 (можно брать любое из предложенных значений, но оговаривая "с вероятностью…").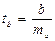 ;
;  ;
; 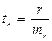 (3.15)
(3.15)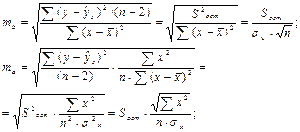 (3.16)
(3.16)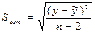 (3.17)
(3.17)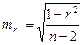 (3.18)
(3.18)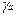 =a ± Da
=a ± Da 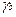 =b ± Db; (3.20)
=b ± Db; (3.20)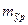 =
= 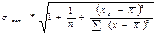 , (3.21)
, (3.21)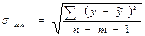 . (3.22)
. (3.22)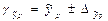 ; (3.23)
; (3.23)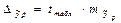 (3.24)
(3.24)


