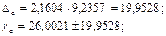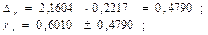Линейная модель.
3. Уравнение однофакторной (парной) линейной регрессии имеет вид:
Для нашего примера: Y – Валовой доход отрасли растениеводства, приходящийся на 100 га пашни (тыс. руб.) (результативный признак); Х – Затраты труда в растениеводстве на 100 га пашни, тыс. чел.-час./га (факторный признак). Для нахождения параметров a и b линейной регрессии можно решить систему нормальных уравнений относительно a и b.
Для расчета параметров уравнения регрессии можно также воспользоваться готовыми формулами, полученными путем преобразования уравнений системы:
Уравнение принимает вид:
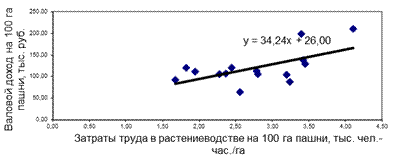
Рисунок 3.1.– Влияние затрат труда в растениеводстве на валовой доход отрасли (линейная модель) Полученное уравнение называется уравнением регрессии, которое характеризует зависимость Валового дохода (у) от затрат труда (х). Коэффициент 34,2 стоящий перед х, называется коэффициентом регрессии. По знаку этого коэффициента судят о направлении связи. Если знак «+» – связь прямая; «-» – связь обратная. Величина коэффициента регрессии показывает, на сколько в среднем изменится величина результативного признака у при изменении факторного признака х на единицу. В данном случае с увеличением затрат труда на 1 чел.-час./га валовой доход увеличивается в среднем на 34,2 тыс. руб.
Подставляя в полученное уравнение регрессии значения xi из исходных данных определяем теоретические (выровненные) значения результативного признака:
Результаты занесем в табл.3.4. Контроль правильности расчетов: 4) Коэффициент регрессии применяется для расчета среднего коэффициента эластичности, который показывает: на сколько процентов в среднем по совокупности изменится результат Y от своей средней величины при изменении фактора X на 1% от своего среднего значения. Формула среднего коэффициента эластичности для парной линейной регрессии принимает вид:
С увеличением затрат труда в растениеводстве на 1 % от своего среднего значения валовой доход увеличивается в среднем на 0,78%.
При линейной корреляции между Х и У исчисляют парный линейный коэффициент корреляции r.
Линейный коэффициент парной корреляции показывает, что связь между затратами труда в растениеводстве и валовым доходом отрасли прямая, умеренная.
Изменение результативного признака У обусловлено вариацией факторного признака Х.
Следовательно, вариация валового дохода на 36% объясняется вариацией затрат труда, а остальные 64% вариации валового дохода обусловлены изменением других, не учтенных в модели факторов.
5) Поверим адекватность построенной статистической модели (т.е. ее соответствие фактическим данным). Оценим модель через среднюю ошибку аппроксимации и F-критерий Фишера. Выполним вспомогательные расчеты (таблица 3.4).
Таблица 3.4. – Расчетные величины
Средняя ошибка аппроксимации равна 20,9%, т.е. в среднем расчетные значения валового дохода отрасли растениеводства, приходящийся на 100 га пашни, отличаются от фактических на 21%, что не входит в допустимый предел. Таким образом, можно сделать вывод, что аппроксимирующая функция подобрана не достаточно удачно.
Проверим модель с помощью F-критерий Фишера. Выдвигаем нулевую гипотезу Но о статистической незначимости уравнения регрессии и показателя тесноты связи (r).
Сравним фактическое значение критерия Фишера с табличным. Для этого выпишем значения критерия Фишера из таблицы «Значения F-критерия Фишера при уровне значимости a=0,05» (приложение5). В нашем примере k1=1; k2=15-1-1=13. Таким образом. Fтабл.=4,67 при a=0,05. Т.к. Fфакт.> Fтабл., то при заданном уровне вероятности a=0,05 следует отвергнуть нулевую гипотезу о статистической незначимости уравнения регрессии и показателя тесноты связи; необходимо признать закономерный характер их формирования. 6. Выдвинем нулевую гипотезу о незначимости коэффициентов корреляции и регрессии. Рассчитаем случайные ошибки параметров линейной регрессии и коэффициента корреляции:
tтабл при уровне значимости α=0,05 и числе степеней свободы, равном 13, равно 2,1604. (приложение 4)
Взаимосвязь между t-статистикой и F-статистикой:
Рассчитаем доверительные интервалы для каждого показателя. Для этого определим предельную ошибку D для каждого из показателей.
С вероятностью 95% можно утверждать, что показатель a находится в пределах: 6,0493< a <45,9549 Так как в пределы доверительного интервала не входит 0, то с вероятностью 95% можно судить о значимости параметра а.
С вероятностью 95% можно утверждать, что коэффициент регрессиинаходится в пределах: 7,9030< b <60,5792 Так как в пределы доверительного интервала не входит 0, то с вероятностью 95% можно судить о значимости коэффициента регрессии.
С вероятностью 95% можно утверждать, что коэффициент корреляциинаходится в пределах: 0,1220< r <1,0000 Так как в пределы доверительного интервала не входит 0, то с вероятностью 95% можно судить о статистической значимости коэффициента корреляции. Полученные оценки уравнения регрессии позволяют использовать его для прогноза.
|

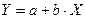


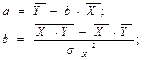


 26+34,24·1,94=92,5313, ц/га;
26+34,24·1,94=92,5313, ц/га;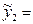 26+34,24·3,45=144,4368, ц/га;
26+34,24·3,45=144,4368, ц/га; 26+34,24·1,83=88,6179, ц/га и т.д.
26+34,24·1,83=88,6179, ц/га и т.д.

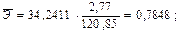
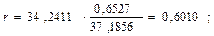
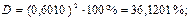


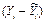
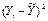
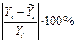

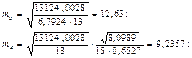
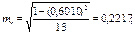

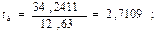

 > tтабл, следовательно нулевая гипотеза о несущественности коэффициентов корреляции и регрессии отвергается, т. е. r и b не случайно отличаются от нуля и сформировались под влиянием систематически действующего фактора х.
> tтабл, следовательно нулевая гипотеза о несущественности коэффициентов корреляции и регрессии отвергается, т. е. r и b не случайно отличаются от нуля и сформировались под влиянием систематически действующего фактора х.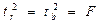 7,35=7,35=7,35
7,35=7,35=7,35