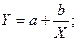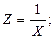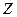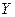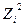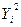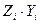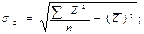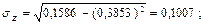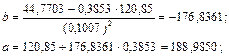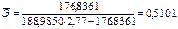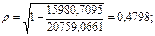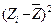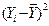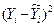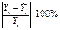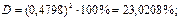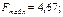Равносторонняя гипербола.

Уравнение равносторонней гиперболы имеет вид:

Данная функция нелинейна относительно переменной, но линейна по параметрам. Прежде, чем проводить анализ необходимо перейти от нелинейной формы к линейной. В регрессиях нелинейных относительно переменных процедура лианеризации (анаморфоза) производится путем замены переменных.

Введем замену:

Вновь полученное уравнение будет иметь вид:

Таблица 3.5. – Расчетные величины, необходимые для определения параметров уравнения

№ хозяйства
	0,5147	111,03	0,2649	12327,8885	57,1452
	0,2901	128,90	0,0842	16614,7449	37,3925
	0,5477	120,31	0,3000	14473,8934	65,8947
	0,3592	112,54	0,1291	12666,1621	40,4304
…	…	…	…	…	…
	0,4398	105,62	0,1934	11156,0468	46,4505
Итого	5,7797	1812,68	2,3784	239812,3499	671,5538
Среднее	0,3853	120,85	0,1586	15987,4900	44,7703

Найдем среднее квадратическое отклонение по Z:

Для расчета параметров уравнения регрессии воспользуемся готовыми формулами:

Уравнение принимает вид:

Коэффициент эластичности рассчитывается по формуле:

С увеличением затрат труда в растениеводстве на 1 % от своего среднего значения валовой доход отрасли растениеводства увеличивается в среднем на 0,5 %.

Для нелинейной модели рассчитывается индекс корреляции:

Для его нахождения выполним вспомогательные расчеты (таблица 3.6).

Индекс корреляции показывает, что связь между затратами труда в растениеводстве и валовым доходом отрасли умеренная. По индексу корреляции нельзя судить о направлении связи.

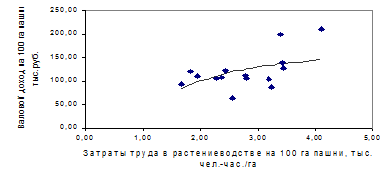
Рисунок 3.2. – Влияние затрат труда в растениеводстве на валовой доход отрасли (гиперболическая модель).

 

Таблица 3.6. – Расчетные величины, необходимые для расчета индекса корреляции и определения показателей аппроксимации

№	Х, тыс. чел.-час./га	У, (тыс. руб.)	Расчетные величины
	1,94	111,03	97,9715	0,0167	96,3172	170,5524	11,7621
	3,45	128,90	137,6860	0,0091	64,8514	77,2256	6,8176
	1,83	120,31	92,1285	0,0264	0,2891	794,0583	23,4225
	2,78	112,54	125,4583	0,0007	68,9085	166,7782	11,4749
…	…	…	…	…	…	…	…
	2,27	105,62	111,2160	0,0030	231,7388	31,2905	5,2960
Итого	41,48	1812,7	1812,712	0,1514	20759,07	15980,71	326,9739
Сред.	2,77	120,85	120,8475	х	х	х	21,7983

Коэффициент детерминации для нелинейных функций рассчитывается следующим образом:

Следовательно, вариация валового дохода отрасли растениеводства, на 23% объясняется вариацией затрат труда в растениеводстве, а остальные 77% вариации валового дохода обусловлены изменением других, не учтенных в модели факторов.

Средняя ошибка аппроксимации равна 21,8%. т.е. в среднем расчетные значения валового дохода отрасли растениеводства, приходящийся на 100 га пашни, отличаются от фактических на 22%, что не входит в допустимый предел. Значит аппроксимирующая функция выбрана неудачно.

Оценим модель через F-критерий Фишера. Выдвинем H₀ о статистической незначимости полученного уравнения регрессии и показателя тесноты связи.

Сравним фактическое значение F-критерия с табличным. Для этого выпишем из таблицы «Значения F-Фишера при уровне значимости α=0,05» табличное значение.

Так как F_факт<F_табл,то при заданном уровне вероятности α=0,05 следует принять нулевую гипотезу о статистической незначимости уравнения регрессии и показателя тесноты связи.

Так как уравнение регрессии является статистически незначимым, расчет прогнозируемого значения валового дохода, приходящегося на 100 га пашни, по данному уравнению не даст достоверного результата.