Зубчатые передачи
5.1.3.1. Цилиндрическая передача Выше была рассмотрена фрикционная передача с гладкими цилиндрическими дисками. Если на этих дисках имеются зубья определенного профиля, расположенные на равном расстоянии один от другого, то передача называется зубчатой цилиндрической (рис. 5.7).
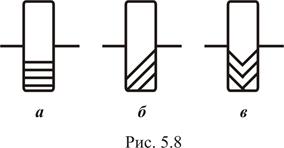
При вращении ведущего зубчатого колеса его зубья взаимодействуют с находящимися с ним в контакте (зацеплении) зубьями ведомого колеса, в результате чего оно также начинает вращаться. Наиболее распространены передачи с эвольвентным зацеплением, при котором профили зубьев выполнены по эвольвенте. Такой профиль позволяет зубьям при вращении колес обкатываться друг по другу, вследствие чего зубчатая передача работает плавно, с небольшими потерями энергии на трение. Зубчатые колеса бывают с прямыми (рис. 5.8, а), косыми (рис. 5.8, б) и шевронными (рис. 5.8, в) зубьями. Косозубые и шевронные колеса обеспечивают более плавный ход передачи, так как в зацеплении находятся одновременно большее число пар зубьев по сравнению с прямозубой передачей. В отличие от ременной и фрикционной передач в зубчатой проскальзывание невозможно, поэтому передаточное отношение, а следовательно и частота вращения ведомого вала всегда постоянны.
Таким образом, для зубчатой передачи передаточное отношение
Однако воспользоваться приведенным соотношением для практического определения передаточного отношения нельзя, так как диаметры воображаемых окружностей (их называют делительные окружности) трудно замерить. Поэтому передаточное отношение необходимо выразить через другие, более удобные для измерений или определений, величины. Зацепление зубчатых колес в передаче требует соблюдения основного условия: зуб одного колеса должен точно входить в соответствующую ему при зацеплении впадину другого колеса. Ширину зуба и впадины, а также другие элементы зацепления рассчитывают по делительным окружностям, на которых основные элементы зубчатого зацепления равны аналогичным элементам зуборезного инструмента (вследствие этого делительные окружности используют при расчетах для настройки зуборезного станка). При изготовлении стандартных зубчатых колес делительная окружность совпадает с начальной окружностью. Таким образом, можно сказать, что зубчатое зацепление возможно лишь при равенстве окружных шагов
Окружной шаг На одном колесе
Передаточное отношение зубчатой передачи выражается через отношение чисел зубьев ведомого и ведущего колес. При наиболее распространенном способе изготовления зубчатых колес – методом обкатки зуборезным инструментом - число зубьев не может быть меньше 17; в противном случае инструмент будет подрезать основание зуба и ослаблять его. Наибольшее число зубьев теоретически не ограничено, однако и здесь есть разумный предел. С учетом этих ограничений установлены оптимальные величины передаточного отношения:
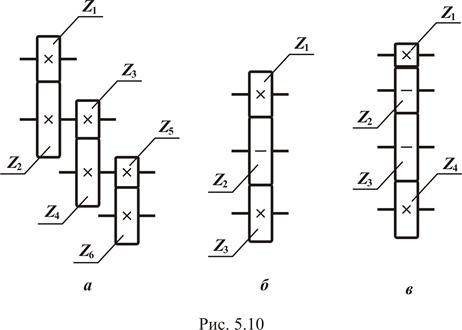
Если иметь в виду наиболее распространенные понижающие передачи (то есть передачи с Например, для трехступенчатой передачи (рис. 5.10, а) общее передаточное отношение равно произведению передаточных отношений отдельных ступеней, то есть
где Кроме простых зубчатых передач, иногда используют передачи с промежуточными зубчатыми колесами. Передачу, показанную на рис. 5.10, б, можно представить как двухступенчатую со ступенями Аналогично передачу, показанную на рис. 5.10, в, будем считать состоящей из трех ступеней: Для нее
Передачи, в которых промежуточные зубчатые колеса не изменяют передаточное отношение, применяют в двух случаях: 1) межосевое расстояние между ведущим и ведомым валами велико для одной пары колес; 2) на ведомом валу необходимо сохранить направление вращения ведущего вала (в этом случае число промежуточных колес должно быть четным). Промежуточное зубчатое колесо, одновременно зацепляющееся с двумя другими так, что по отношению к одному является ведомым, а по отношению к другому - ведущим, называется паразитным; 3) если в одной конструкции объединить рассматриваемые схемы (см. рис 5.10, б и рис 5.10, в), то получится реверсивный механизм, с помощью которого при неизменном направлении вращения ведущего вала ведомый вал будет изменять направление вращения в зависимости от числа включенных колес - четного или нечетного.
|

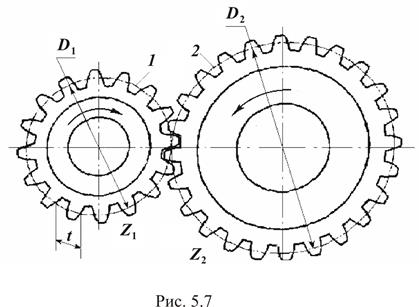
 Если при вращении зубчатых колес представить себе в передаче две касающиеся окружности 1 и 2 диаметрами
Если при вращении зубчатых колес представить себе в передаче две касающиеся окружности 1 и 2 диаметрами 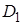 и
и 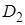 (см. рис. 5.7), которые катятся одна по другой без скольжения, – это позволит распространить на зубчатую передачу основные кинематические закономерности фрикционной передачи.
(см. рис. 5.7), которые катятся одна по другой без скольжения, – это позволит распространить на зубчатую передачу основные кинематические закономерности фрикционной передачи.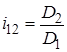 .
.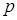 , измеренных по дугам делительных окружностей (см. рис. 5.9).
, измеренных по дугам делительных окружностей (см. рис. 5.9).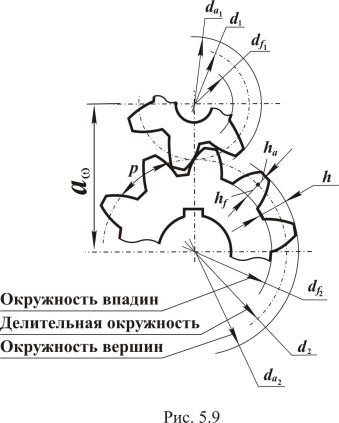
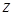 .
. , на другом -
, на другом - 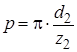 . Следовательно,
. Следовательно,  . Так как
. Так как  , то окончательно можно сделать вывод, что
, то окончательно можно сделать вывод, что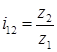 .
.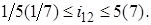
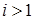 ), то намного увеличить передаточное отношение можно только путем создания многоступенчатых передач.
), то намного увеличить передаточное отношение можно только путем создания многоступенчатых передач.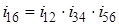 ,
,


 и
и 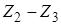 , то есть считать, что колесо Z 2 для первой ступени ведомое, а для второй - ведущее. В этом случае общее передаточное отношение
, то есть считать, что колесо Z 2 для первой ступени ведомое, а для второй - ведущее. В этом случае общее передаточное отношение 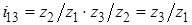 .
. .
.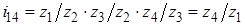 .
.