Геометрические элементы зубчатого зацепления
Шаг зубчатой передачи (расстояние между одноименными сторонами двух соседних зубьев колеса, измеренное по делительной окружности)
Значения модуля, являющегося основной геометрической характеристикой зубчатого колеса, стандартизованы, что облегчает изготовление и подбор зубчатых колес. Расстояние от делительной окружности до вершины зуба называется высотой головки зуба Для цилиндрического зубчатого колеса можно легко определить основные размеры: диаметр делительной окружности диаметр окружности вершин диаметр окружности впадин расстояния между центрами колес Модуль готового колеса легко определить, измерив диаметр окружности вершин и разделив его на число зубьев, увеличенное на два (с последующим округлением до ближайшей стандартной величины), то есть
Приведенные выше зависимости справедливы только для прямозубых колес. Геометрический расчет косозубых и шевронных колес более сложен и здесь не приводится.
|
. Отсюда можно определить диаметр делительной окружности (см. рис. 5.9) 
. Для первого колеса 
, для второго -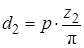 
. Поскольку величина 
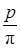, имеющаяся в обоих выражениях, не может быть подсчитана точно, более удобно взамен ее ввести величину 
[мм], называемую модулем зубчатого колеса:
.
(см. рис. 5.9), а от делительной окружности до основания зуба - высотой ножки зуба 
.
;
;
.
.
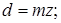
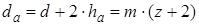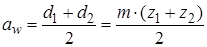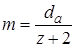