Гл. 5 Поверхности второго порядка.
Всякое уравнение По виду уравнения поверхности разделяются по виду:
10. Алгебраические, где функция
Пример:
20. Трансциндентные поверхности- все остальные.
пример трансциндентной поверхности Поверхности второго порядка в пространстве называется множество точек координаты которых удовлетворяют уравнению Общий вид многочлена:
где Оказывается, что подходящим выбором координат любое уравнение второй степени сложно привести к каноническому уравнению, то есть к одному из следующих видов поверхностей.
|
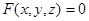между декартовыми координатам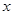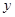и 
, 
и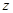 
определяют некоторую поверхность в пространстве.
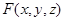- многочлен некоторой степени, относительно 
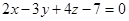- поверхность первого порядка (плоскость).
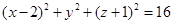- поверхность второго порядка (сфера).
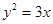- поверхность второго порядка (параболический цилиндр).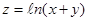
,
, 
, 
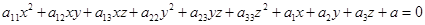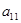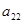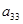- одновременно в ноль не обращаются.
