Симметрии твердых тел

Основы физики твердых тел

Симметрии твердых тел

Твердые тела. Наиболее характерной особенностью твердых тел, отличающих их, как агрегатное состояние вещества от других агрегатных состояний, является сохранение формы и объема. Благодаря этому твердые тела сыграли главную роль при формировании в сознании человека понятий пространства, геометрических образов и соотношений между ними, а также в развитии теории измерения пространства. Движение твердых тел явилось той основой, на которой были выработаны понятия о механическом движении и перемещении материальных объектов.

Место, занимаемое материальным телом, и его форма абстрагируются в нашем понятии в виде самостоятельных геометрических пространственных образов. Благодаря этому приобретает смысл представление о сравнении твердых тел по их форме, размеру и т.д.

Очень важным геометрическим свойством твердых тел является их симметрия. Например, найденный на дороге камень отличается от кирпича в первую очередь тем, что он имеет неправильную форму. Слова «правильная» и «неправильная» форма являются субъективным отражением объективных свойств форм материальных тел, а именно их симметрии.

Мы говорим, что прямой цилиндр более симметричен, чем прямоугольный параллелепипед, а шар более симметричен, чем цилиндр. Мы говорим также, что внешняя форма человеческого тела, я также тела большинства животных симметричны. Задача состоит в том, чтобы дать математическую формулировку понятию симметрии.

Определение симметрии. Под симметрией понимается способность твердого тела совмещаться с самим собой в результате его движения или воображаемых операций над его точками. Чем большим числом способов такое совмещение возможно, тем более симметричной является форма тела.

Например, прямой круглый цилиндр совмещается с самим собой при повороте вокруг своей оси на любой угол. Он также совмещается с самим собой при повороте на угол в 180° вокруг любой оси, перпендикулярной оси цилиндра, проведенной через точку оси на половине высоты цилиндра. Если же взять шар, то он может быть совмещен с самим собой при повороте его на любой угол вокруг любой оси, проходящей через центр шара. Ясно, что возможностей для совмещения шара с самим собой значительно больше, чем для цилиндра. Именно этот факт выражается в утверждении, что шар является телом более симметричным, чем прямой круглый цилиндр.

Однако к совмещениям тела с самим собой только с помощью пространственных движений симметрия не сводится. Например, левая половина человеческого тела никакими пространственными движениями не может быть совмещена с правой. Другими словами, на левую руку нельзя надеть правую перчатку. Под симметрией левой и правой рук понимают не возможность совмещения левой руки с правой в результате пространственного совмещения, а возможность совмещения правой руки с отражением левой руки в плоском зеркале.

Несмотря на кажущееся чрезвычайно большое многообразие возможностей симметрии твердых тел, все они складываются из четырех элементов. Различные комбинации этих четырех элементов симметрии и составляют всевозможные симметрии твердых тел.

Ось симметрии п- го порядка. Если тело совмещается само c собой при повороте вокруг некоторой оси на угол 2p¤ п, то эта ось называется осью симметрии п-го порядка. Например, квадратный цилиндр (рис. 4.1) совмещается с самим собой при повороте на угол p/2 вокруг оси, проходящей через точки пересечения диагоналей квадратов, образующих его основание. Следовательно, эта ось является только осью 4-го порядка. Нет необходимости доказывать, что любая ось тела является осью 1-го порядка.

Плоскость симметрии. Если тело совмещается само с собой в результате зеркального отражения его точек в некоторой плоскости, то эта плоскость называется плоскостью симметрии тела. На рис. 4.2 заштрихованная поверхность – плоскость симметрии.

Рис. 4.2

 

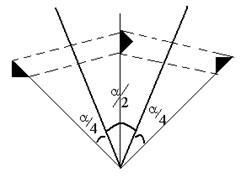
Центр симметрии. Если тело совмещается с самим собой при инверсии относительно некоторой точки, то эти точки называются центром симметрии (т. О на рис. 4.1).

Точечные группы симметрии. Совокупность элементов симметрии тела называется его группой симметрии. Рассмотренные элементы симметрии характерны тем, что они оставляют неподвижной по крайней мере одну точку тела. Соответствующие им группы симметрии называются точечными. Все перечисленные симметрии можно описать с помощью одних только отражений в плоскости. Поворот на угол a можно представить в виде двух последовательных отражений в плоскостях, пересекающихся на оси поворота под углом a/2 (рис.4.3). Инверсия относительно центра симметрии сводится к трем отражениям в трех взаимно перпендикулярных плоскостях, проходящих через центр симметрии.

Рис. 4.3

 

Зеркальные изомеры. Два тела могут быть похожими друг на друга и могут быть совмещены друг с другом с помощью отражения в плоскости, однако, они не могут быть совмещены друг с другом никакими пространственными движениями. В качестве примера укажем на кисти человеческих рук. Такие тела называются зеркальными изомерами. Известны многие молекулы, являющиеся зеркальными изомерами. Они отличаются по своим свойствам в том же смысле, в каком правое отличается от левого. Например, они в разных направлениях вращают плоскость поляризации света, проходящую через них, если только такое вращение вообще имеет место. Химические реакции между одноименными зеркальными изомерами проходят по-другому, чем между разноименными. Например, правый изомер одного вещества с правым изомером другого реагирует иначе, чем правый с левым.