Теплоемкость твердых телКлассическая теория. Моделью является кристаллическое твердое тело, атомы которого колеблются около положений равновесия в узлах кристаллической решетки. Каждый атом может независимо колебаться в трех взаимно перпендикулярных направлениях, являясь относительно этого направления линейным осциллятором. В соответствии с законом о равнораспределении энергии по степеням свободы средняя энергия осциллятора равна kT. Эта энергия состоит из кинетической kT/2 и потенциальной kT/2 энергий. Таким образом, тело, состоящее из n атомов, вследствие теплового движения обладает энергией U=3nkT, (4.8) а теплоемкость этого тела равна Сv =(dU/dT)v=3nk,(4.9) т.е. теплоемкость твердого тела является величиной постоянной. Если взять моль молекул вещества, то n является постоянной Авогадро NA, nk = R (где R - молярная газовая постоянная). Формула (4.9) показывает, что молярная теплоемкость равна 3 R и не зависит от температуры. Это закон Дюлонга и Пти. Этот закон утверждает, что молярная теплоемкость всех химических простых твердых тел одинакова и равна 3 R. Этот закон выполняется достаточно хорошо только при сравнительно высоких температурах. Теплоемкость при низкой температуре. Опыты по измерению теплоемкости при низкой температуре показали, что она зависит от температуры. При приближении температуры к 0 К теплоемкость стремится к нулю по степенному закону Cv ~ T3. Полученная в экспериментах зависимость теплоемкости от температуры изображена на рис. 4.17. Заметим, что такое поведение теплоемкости от температуры наблюдается лишь у неметаллических твердых Модель Эйнштейна. Чтобы объяснить поведение теплоемкости в зависимости от температуры, А. Эйнштейн в 1907 г. предложил воспользоваться соображениями о дискретном характере энергий, которыми могут обладать осцилляторы, образующие твердое тело, подобно тому, как это было сделано ранее М. Планком для вывода формулы излучения абсолютно черного тела. Пусть «элементарная» порция энергии, которой может обладать линейный осциллятор, равна ε. Эту энергию можно считать связанной с некоторой частотой колебаний осциллятора таким же соотношением, каким энергия фотона связана с его частотой ε = Вообще говоря, ниоткуда не следует, что минимальная энергия осциллятора равна нулю. Обозначим ее ε0. Для расчета теплоемкости ее точное значение не играет роли. Поэтому возможные энергии, которыми может обладать осциллятор, представляются в виде εn = ε0 + n ε (n= 0,1,2,…). (4.11) Естественно предположить, что вероятность Pn состояния осциллятора с энергией ε n задается формулой Больцмана. Поэтому можно написать Pn=A exp[ - ε n /(kT)] =A exp[-(ε 0+n ε)/(kT)], (4.12) где А – нормированная постоянная, определяемая условием нормировки вероятности
Теперь можно вычислить среднюю энергию осциллятора
По формуле для геометрической прогрессии
Дифференцируя обе части этого равенства по ε, получаем
Следовательно, выражение (4.14) принимает вид:
(Примечание: Движение совокупности связанных между собой осцилляторов описывается посредством учета нормальных мод колебаний системы, которые далее будут рассмотрены подробно). Носителем энергии при этом является не отдельный осциллятор, а нормальная мода колебаний системы в целом, которая рассматривается как квазичастица, называемая фононом. Фононы и другие квазичастицы, являющиеся нормальными модами соответствующих возбуждений (магноны, поляритоны, экситоны и т.д.), не являются частицами в том же смысле, в каком являются частицами фотоны, хотя математические схемы описания их поведения могут иметь много общего.) Отсюда для энергии колебаний одного моля осцилляторов получаем
Тогда теплоемкость при постоянном объеме
Это формула Эйнштейна для теплоемкости. В качественном смысле поведение теплоемкости в зависимости от температуры по этой формуле согласуется с экспериментами, результаты которых представлены на рис. 4.17. Действительно, из формулы (4.19 а) видно, что при достаточно большой температуре,
Температура Эйнштейна. «Элементарная порция энергии» ε зависит от свойств вещества твердого тела, причем с увеличением «жесткости» вещества эта величина возрастает, поскольку увеличивается частота ω колебаний в формуле (4.10). Эту энергию принято характеризовать посредствам температуры Эйнштейна (Θ э), определяемой соотношением k Θ э = ε. (4.19 б) Формула (4.1 а) может быть переписана:
Недостаточность теории Эйнштейна. Однако в количественном отношении формула (4.19 а) не согласуется с экспериментом, потому что она предсказывает экспоненциальное уменьшение теплоемкости CV ~ exp[-ε/(kT)] при приближении к 0 К, а эксперимент дает лишь степенное уменьшение Таким образом, модель Эйнштейна для расчета теплоемкости не точна и должна быть существенно усовершенствована. Наряду с указанным выше количественным несогласием результатов этой теории с экспериментом следует отметить ее другой недостаток, имеющий принципиальный характер. Считается, что твердое тело есть совокупность независимых линейных осцилляторов, энергии которых задаются формулой (4.11), т.е. движения атомов в твердом теле считаются столь же независимыми друг от друга, как движения атомов и молекул в газах. Но это заведомо неправильно, поскольку само удержание атомов около некоторых положений равновесия есть результат взаимодействия атомов между собой. Поэтому в твердом теле нельзя рассматривать атомы как независимые, необходимо принять во внимание их коллективные взаимодействия. Именно учет этого взаимодействия атомов приводит к теории теплоемкости, согласующейся с экспериментом. Элементарные возбуждения. Система атомов, составляющих твердое тело, при 0 К находится в основном состоянии с минимальной энергией. Чтобы проанализировать теплоемкость вблизи 0 К, необходимо найти те энергии, которые может иметь система атомов вблизи 0 К. Предположим, что некоторый атом в результате сообщения ему энергии извне движется из положения равновесия в некотором направлении. Сила, стремящаяся вернуть его в положение равновесия, есть просто сила отталкивания со стороны других атомов решетки. Поэтому, выходя из положения равновесия, атом действует с определенными силами на соседние атомы, которые в свою очередь должны покинуть свои положения равновесия, в результате чего движения атомов приобретают коллективный характер. Такое коллективное движение атомов, когда смещение одного атома передается соседнему, затем следующему соседнему и т.д., есть не что иное, как звуковая волна в твердом теле. Таким образом, элементарными возбуждениями являются звуковые колебания. Нормальные моды. С учетом только что описанного взаимодействия система атомов должна рассматриваться как совокупность связанных осцилляторов. В этом случае любое движение системы атомов может быть представлено как суперпозиция нормальных колебаний или нормальных мод системы. Каждая из нормальных мод кроме прочего характеризуется своей частотой, а энергия этой моды задается формулой (4.10), т.е. мода частоты ω i имеет энергию εi = где постоянная для всех мод энергия ε0 отброшена. В данном твердом теле может быть возбуждено одно, два колебания (и больше) данной моды. Если возбуждено n колебаний данной моды, то полная энергия этих n колебаний, очевидно, равна εin = n Вероятность того, что с данной модой связана полная энергия ε in, считается подчиняющейся распределению Больцмана и, следовательно, Pn = A exp[-ε in /(kT)] = A exp[ n где А – нормировочный множитель. Эта формула аналогична (4.12). С ее помощью можно вычислить среднюю энергию, приходящуюся на рассматриваемую моду, а разделив эту энергию на энергию одного колебания моды, можно сразу же получить среднее число <ni>; колебаний данной моды, которые возбуждены. Вычисления совершенно аналогичны в математическом смысле, которые привели от формулы (4.12) к формуле (4.17), и дают следующий результат:
Теперь вопрос вычисления полной энергии возбуждения свелся к нахождению частот нормальных мод и их числа. Фононы. Выражение (4.20) для энергии, связанной с модой колебаний частоты ω i, по аналогии с соответствующей формулой для энергии фотонов, наводит на мысль рассматривать такую моду, как квазичастицу. Это представление было, в сущности, уже использовано, когда в (4.22) формула Больцмана была применена для определения средней энергии в моде. Такая квазичастица, связанная с модами звуковых колебаний, называется фононом. Введение понятия фононов является плодотворным приемом, значительно облегчающим рассуждения. Оно также весьма эффективно с чисто математической точки зрения, так как формальные математические приемы вычисления различных величин, связанных с фононами, аналогичны соответствующим вычислениям, относящимся к фотонам. Эта аналогия обуславливается тем, что в обоих случаях мы имеем математически одинаковые волновые процессы. Однако физическая сущность этих процессов совершенно различна. Поэтому из факта существования фотонов как частиц, которые обладают соответствующей энергией, обнаруживаемой экспериментально, и могут существовать изолированно, отнюдь не следует, что и фононы являются частицами с аналогичными свойствами. В современной физике имеется большое число других аналогичных квазичастиц, являющихся нормальными модами соответствующих возбуждений (магноны, поляритоны, экситоны и т. д.). Сказанное выше о фононах справедливо также и относительно этих квазичастиц. Модель Дебая. В твердом теле возможно распространение продольных и поперечных волн с различными скоростями. Поперечные волны могут иметь два различных направления поляризации. Таким образом, можно говорить просто о длинноволновых модах звуковых волн с тремя различными поляризациями, каждая из которых, вообще говоря, различна и может зависеть от направления распространения волны. Однако для упрощения будем рассматривать случай изотропного твердого тела. Вычисление числа мод для каждой поляризации совершенно одинаково. Теория теплоемкости Дебая основывается на расчете числа мод звуковых колебаний твердого тела. К сказанному выше следует лишь добавить, что речь идет о достаточно длинноволновых модах, поскольку возбуждения вблизи температуры 0 К и частоты колебаний должны соответствовать достаточно малым энергиям, т.е. быть малыми.
Напишем закон сохранения массы в объеме: изменение массы в объеме, отнесенное ко времени: d(
где последняя величина разложена в ряд Тейлора и сохранен лишь первый член, линейный по
называемое уравнением непрерывности. Сила, которая действует на массу в рассматриваемом объеме, обуславливается разностью давлений p на разные стенки цилиндра. Следовательно, уравнение Ньютона имеет вид:
или
Изменения плотности и давления в среде можно считать малыми:
где Подставляя (4.28) в уравнение (4.25) и (4.27) и сохраняя лишь линейные по
Этих двух уравнений недостаточно для определения трех неизвестных величин p = p (r). (4.30)
Соотношения (4.28) с учетом (4.30) имеют вид:
т.е.
где
Как будет видно из дальнейшего, v является скоростью распространения волн. С помощью (4.32) можно исключить p’ из уравнений (4.29), в результате чего они принимают такой вид:
Продифференцировав первое из уравнений (4.34) по t, а второе – по x, и вычитая первое уравнение из второго, находим
Аналогично, дифференцируя первое из уравнений (4.34) по x, а второе –по t, и вычитая почленно одно из другого, имеем
Уравнения (4.35) и (4.36) описывают волну, распространяющуюся вдоль оси X со скоростью v. Это непосредственно видно из того, что любая функция f(t-x/v) является решением этого уравнения. Поэтому фронт волны f = const задается условием t–x/v = const, (4.37) из которого следует, что (dx/dt) = v, (4.38) т.е. v является действительно скоростью распространения фронта волны. Решение уравнений (4.35) и (4.36) будем искать в следующем виде:
Подставляя (4.39) в (4.34), получаем алгебраические уравнения для определения
откуда
Соотношение (4.42) выражает связь существующую между частотой волны ω = 2π/ T и волновым числом k = 2π/λ, где T и λ – период колебаний и длина волны. Это соотношение называется дисперсионным. В данном случае оно имеет простой вид. Однако в других случаях оно может быть более сложным. Это соотношение позволяет определить частоты колебаний, а следовательно, и энергии соответствующих мод, если известны волновые числа. Определение числа мод. В теле конечного размера возникают стоячие волны. Границы тела свободно колеблются, на них никакие напряжения не возникают. Возьмем тело в виде куба объемом L3 и поместим начало координат в одну из вершин. Рассмотрим плоские стоячие волны по оси X. Обозначим ξ - отклонение колеблющейся точки от положения равновесия. Поскольку поверхность куба свободна, на ней при колебаниях не возникают никакие напряжения, т.е. граничное условие имеет вид:
Решение уравнения (4.36), удовлетворяющее условиям (4.43), имеет вид:
где ω и k связаны равенством (4.42). Для того чтобы удовлетворить (4.43), надо в (4.44) положить A = 0, а на k наложить условие kL = n π, (n= 1, 2 …). Оно определяет дискретный набор волновых чисел, при которых возможно существование стоячих волн. Аналогичные формулы находятся и для других осей координат. Следовательно, получаем следующие наборы волновых чисел, каждому из которых соответствует стоячая волна, составляющая моду колебаний: kx = π nx/L, ky = π ny/L, kz = π nz/L (4.45) (nx=1,2,…), (ny=1,2,…), (nz=1,2,…), Числа nx, ny, nz пробегают все возможные значения независимо. Подсчет числа мод сводится к определению числа различных троек числа (nx, ny, nz) или, другими словами, к подсчету числа точек, декартовы координаты которых равны (nx, ny, nz). Число этих точек в объеме с длинами сторон
Для подсчета dN удобнее перейти к сферическим координатам (рис.4.3), принимая во внимание, что kx, ky, kz имеют лишь положительное значение. Это означает, что в (4.46) надо положить dkxdkrdkz = (4 π /8)k2dk. В результате для числа мод в интервале волновых чисел от k до k+dk (4.39) получаем выражение
где множитель 4π сохранен без сокращения на (2π3) в знаменателе для того, чтобы подчеркнуть произведенный переход к сферическим координатам. Далее воспользуемся соотношением (4.42), из которого следует, что k2dk=(1/v3) ω2 d ω (4.48) и, следовательно, число мод с частотой колебаний между ω; и ω+ d ω равно
Плотность мод. Число мод, отнесенное к интервалу частот, называется плотностью мод ρ(ω) = dN/d ω. (4.50)
Поэтому из (4.9) следует, что
Аналогичные расчеты можно провести для каждой из поперечных мод. В изотропном случае скорости обеих поперечных мод одинаковы. Обозначив скорости продольной и поперечной мод соответственно v при v пп и приняв во внимание, что плотность всех мод равна сумме плотностей отдельных мод, напишем
Чтобы не усложнять обозначения в (4.52), полная плотность мод показана той же буквой, какой раньше в (4.51) была обозначена плотность мод одной из поляризаций. Отметим, что по самому смыслу предшествующих расчетов формула (4.52) не может быть справедливой для очень коротких длин волн, поскольку мы пренебрегли атомной структурой твердого тела и проводили расчет так, как если бы оно состояло из непрерывно распределенной по его объему массы. Для волн, длина которых существенно превосходит среднее расстояние между атомами, а смещение атомов из положения равновесия не очень велики, формула (4.52) является справедливой. Именно этот случай и интересен при рассмотрении теплоемкости при низкой температуре. С другой стороны, поскольку температура и kT очень малы, выражение (4.52) справедливо вплоть до частот, для которых Теплоемкость при низкой температуре. Полная энергия всех мод колебаний, связанная с тепловой энергией, равна Входящий в это выражение интеграл может быть вычислен методами функций комплексного переменного. Он равен Формула (4.53) позволяет вычислить теплоемкость
Такая зависимость теплоемкости от температуры вблизи температуры 0 К согласуется с данными эксперимента. Температура Дебая. Строго говоря, все проведенные расчеты, в частности вывод дисперсионного соотношения, справедливы только для волн с достаточно большой длиной волны. Поэтому полученная на основе дисперсного соотношения формула (4.52) также справедлива лишь для таких же волн, т.к. для не слишком больших частот. Однако из замечаний о вкладе в теплоемкость волн с короткой длиной волны, сказанных в связи с формулой (4.52), следует, что мы не сделаем большой ошибки, если применим эту формулу также и для больших частот, вплоть до максимальной частоты ωмакс, определенной таким образом, чтобы полное число мод при этом было равно фактически имеющемуся числу мод 3 NA. Поэтому
Максимальная частота ωмакс зависит от упругих свойств материала. Вообще говоря, частота ωмакс может быть различной для различных направлений поляризации. Однако для упрощения формулы в (4.55) взята некоторая средняя максимальная частота. Подставив выражение (4.52) в (4.55) и проинтегрировав, получим
где < v>; - средняя скорость звука, определяемая соотношением
Максимальную частоту, определенную в соответствии с условием (4.55), принято выражать через температуру Дебая k Обычно температура Дебая лежит в пределах от 100 до 1000 К. Например, для меди она равна примерно 340 К, а для алмаза – около 2000 К. Теплоемкость при произвольной температуре. При вычислении энергии U в (4.53) не учитывалось наличие максимальной частоты ωмакс, определяемой формулой (4.55). Если это учесть, то интеграл необходимо ограничить частотой ωмакс. Тогда вместо формулы (4.53) получим
где < v > определяется соотношением (4.57). Переходя при интегрировании к безразмерной переменной ξ = и принимая во внимание (4.56) и (4.58), получаем
Теплоемкость CV находим дифференцированием (4.54) по Т. При Т<<;θDверхний предел интегрирования может быть распространен до При Т >>θDверхний предел интегрирования близок к нулю и, следовательно, ξ в подынтегральном выражении очень малая величина, и можно считать, что exp
Следовательно, теплоемкость в этом случае равна CV = (dU/dT) v = 3 R, (4.62) т.е. так и должно быть в соответствии с законом Дюлонга и Пти. При температуре T ~ Вывод формул для теплоемкости, исходя из представления о фононах. Для того чтобы освоиться с представлением о квазичастицах, полезно вывести формулу для теплоемкости твердого тела на основании представления о фононах. Как уже было отмечено в связи с формулой (4.20), моду колебаний, несущую энергию Энергия фонона в соответствии с (4.20) равна ε = а его импульс p связан с волновым числом k обычным соотношением для свободных частиц p = Энергия и импульс фонона связаны соотношением (4.42), которое с учетом (4.63) и (4.64) может быть записано в виде ε = < где учтено наличие нескольких поляризаций фононов и взята их средняя скорость в соответствии с (4.57). Плотность состояний газа, состоящего из фононов как квазичастиц, дается формулой в виде dГ = ρ(ε) d ε = 3V4 π p2dp/(2 π h)3. (4.66) Множитель 3 учитывает три возможных поляризации фононов. Принимая во внимание (4.64), из (4.57) получаем
Для дальнейших вычислений удобно выразить ρ(ε) не через среднюю скорость < v > звука, а через температуру Дебая, воспользовавшись условием, что общее число фононов должно быть равно
Тогда ρ(ε) = 9NA ε 2/(k θ D)3. (4.69) Фононы являются частицами, подчиняющимися статистике Бозе-Эйнштейна, и поэтому среднее число < n>; фононов с энергией ε дается формулой, которая в данном случае записывается виде < n( ε)> = {exp[ε/(kT)-1}-1. (4.70) Для полной энергии фононов в теле получаем выражение
что, как и следовало ожидать, совпадает с формулой (4.60). Приведенный вывод показывает, что представление о квазичастицах, в данном случае фононах, позволяет пользоваться понятиями и математическими приемами, выработанными для реальных частиц. Однако отсюда не следует делать вывод, что квазичастицы существуют в том же смысле, в каком существуют реальные частицы. Например, в приведенном выше выводе формулы теплоемкости мы обращались с фотоном точно так же, как с фотоном при выводе формулы абсолютно черного тела. Тем не менее, нельзя назвать фонон элементарной частицей в том же смысле, в каком фотон является одной из фундаментальных элементарных частиц физики. В этом случае к теплоемкости за счет колебаний кристаллической решетки добавляется теплоемкость за счет свободных электронов металла. При обычной температуре она составляет ничтожную часть решеточной теплоемкости и может не приниматься во внимание. Однако с понижением температуры, поскольку решеточная теплоемкость убывает как ~ T 3, а электронная – как ~ T, ее роль возрастает и при достаточно низкой температуре электронная теплоемкость играет главную роль по сравнению с решетчатой.
|

 тел, у которых единственной энергией, связанной с тепловым движением, является энергия колебаний атомов в узлах кристаллической решетки. У металлических тел имеются свободные электроны, часть которых также участвует в тепловом движении и дает вклад в теплоемкость. Однако этот вклад невелик, поскольку в тепловом движении участвует лишь небольшая доля электронов, энергии которых лежат вблизи энергии поверхности Ферми. Лишь при низкой температуре, когда вклад в теплоемкость, связанный с движением атомов сильно уменьшается, электронная теплоёмкость становится главной.
тел, у которых единственной энергией, связанной с тепловым движением, является энергия колебаний атомов в узлах кристаллической решетки. У металлических тел имеются свободные электроны, часть которых также участвует в тепловом движении и дает вклад в теплоемкость. Однако этот вклад невелик, поскольку в тепловом движении участвует лишь небольшая доля электронов, энергии которых лежат вблизи энергии поверхности Ферми. Лишь при низкой температуре, когда вклад в теплоемкость, связанный с движением атомов сильно уменьшается, электронная теплоёмкость становится главной.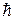 ω. (4.10)
ω. (4.10)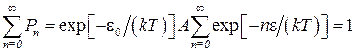 . (4.13)
. (4.13)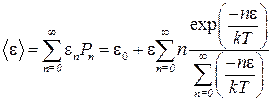 . (4.14)
. (4.14) . (4.15)
. (4.15) . (4.16)
. (4.16) . (4.17)
. (4.17) . (4.18)
. (4.18)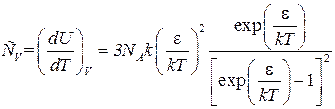 . (4.19 а)
. (4.19 а)
 а при
а при  получаем
получаем
 . (4.19 в)
. (4.19 в) . (4.23)
. (4.23) Дисперсионное соотношение. Прежде всего выведем волновое уравнение, например, для продольных волн, распространяющихся вдоль оси X (рис. 4.18). Пусть имеется тонкий цилиндр, площадь основания которого S и высота
Дисперсионное соотношение. Прежде всего выведем волновое уравнение, например, для продольных волн, распространяющихся вдоль оси X (рис. 4.18). Пусть имеется тонкий цилиндр, площадь основания которого S и высота 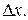 Обозначим:
Обозначим:  (x,t) –плотность вещества, а p(x,t) - давление, которое в нем возникает в результате изменения плотности; u(x, t) – скорость колебаний частиц вещества вдоль оси X. Эта скорость не является скоростью распространения волны, а во много сотен раз меньше ее.
(x,t) –плотность вещества, а p(x,t) - давление, которое в нем возникает в результате изменения плотности; u(x, t) – скорость колебаний частиц вещества вдоль оси X. Эта скорость не является скоростью распространения волны, а во много сотен раз меньше ее. ) /dt, равно разности масс, вошедших в объем и вышедших из него
) /dt, равно разности масс, вошедших в объем и вышедших из него (4.24)
(4.24) Остальные члены можно отбросить, поскольку дальше
Остальные члены можно отбросить, поскольку дальше  , (4.25)
, (4.25)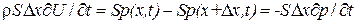 (4.26)
(4.26)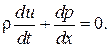 (4.27)
(4.27) (4.28)
(4.28) и
и  - постоянные плотность и давление в среде при отсутствии волны:
- постоянные плотность и давление в среде при отсутствии волны:  и
и 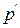 - изменения плотности и давлении, связанные с волной. Обе эти величины являются малыми. Все дальнейшие вычисления проводятся с сохранением величин первого порядка малости по
- изменения плотности и давлении, связанные с волной. Обе эти величины являются малыми. Все дальнейшие вычисления проводятся с сохранением величин первого порядка малости по 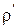 и
и 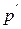 .
.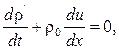
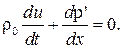 (4.29)
(4.29) и u. Необходимо иметь еще одно уравнение, содержащее эти величины. Им является уравнение состояния, связывающее давление и плотность
и u. Необходимо иметь еще одно уравнение, содержащее эти величины. Им является уравнение состояния, связывающее давление и плотность (4.31)
(4.31) (4.32)
(4.32) (4.33)
(4.33) (4.34)
(4.34)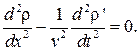 (4.35)
(4.35)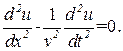 (4.36)
(4.36)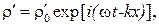
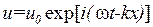 . (4.39)
. (4.39)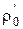 и
и  :
:
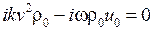 (4.40)
(4.40) ,
,  , (4.41)
, (4.41) . (4.42)
. (4.42) (4.43)
(4.43) (4.44)
(4.44) ,
, 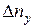 и
и  равно
равно 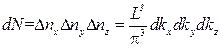 , (4.46)
, (4.46) где
где 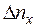 = (L/π)dkx и т.д., как это непосредственно следует из (4.45). В правой части (4.46) написаны дифференциалы dkx, dky, dkz, потому что L много больше длины волн.
= (L/π)dkx и т.д., как это непосредственно следует из (4.45). В правой части (4.46) написаны дифференциалы dkx, dky, dkz, потому что L много больше длины волн.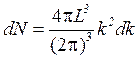 , (4.47)
, (4.47)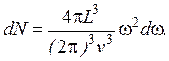 . (4.49)
. (4.49) . (4.51)
. (4.51)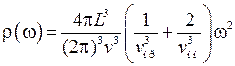 . (4.52)
. (4.52) ω >> kT. В этой области exp[
ω >> kT. В этой области exp[ 
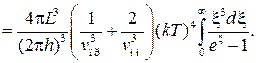 (4.53)
(4.53)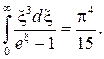
 (4.54)
(4.54)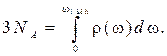 (4.55)
(4.55) , (4.56)
, (4.56)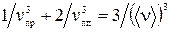 . (4.57)
. (4.57) получаемую из соотношения
получаемую из соотношения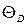 =
= 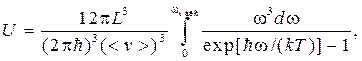 (4.59)
(4.59)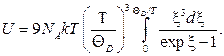 (4.60)
(4.60) , тогда получаем (4.54).
, тогда получаем (4.54). Поэтому формула (4.60) принимает вид:
Поэтому формула (4.60) принимает вид: . (4.61)
. (4.61) интеграл в (4.52) не может быть вычислен аналитически и приходится пользоваться численными методами. Свойства различных материалов учитываются значением температуры Дебая
интеграл в (4.52) не может быть вычислен аналитически и приходится пользоваться численными методами. Свойства различных материалов учитываются значением температуры Дебая 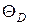 . Поэтому кривая теплоемкости как функция отношения T/
. Поэтому кривая теплоемкости как функция отношения T/  > p, (4.65)
> p, (4.65) (4.67)
(4.67)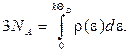 (4.68)
(4.68)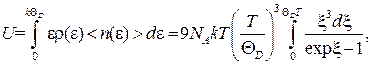 (4.71)
(4.71)


