Кристаллические решетки
Необходимость периодической структуры. Твердое состояние возникает при столь сильном взаимодействии между молекулами (атомами или ионами), что тепловое движение молекул не играет в структуре столь значительную роль, которую оно играет в жидкостях и особенно в газах. В результате этого молекулы располагаются друг относительно друга в некоторых фиксированных с большой точностью положениях, осуществляя небольшие тепловые колебания около положений равновесия. Взаимное расположение точек равновесия определяется условиями равновесия. Ясно, что если эти условия равновесия выполнены в некоторой области пространства и обусловили взаимное расположение молекул в этой области пространства, то они должны быть выполнены в другой области и, следовательно, должны обусловить аналогичное расположение молекул в другой области пространства. А это означает, что взаимное расположение молекул повторяется при переходе из одних областей пространства в другие, т.е. структура твердых тел периодическая. Она реализуется в виде кристаллической решетки, а сами твердые тела являются кристаллами. Точки равновесия составляющих кристаллы атомов, молекул или ионов называются узлами кристаллической решётки. Однако, при такой аргументации возникает вопрос о причинах существования аморфных твёрдых тел, таких, как стекло, пластик, и аналогичных веществ без периодической структуры. Ответ состоит в том, что они не находятся в равновесном состоянии и с течением времени изменяют свою структуру, приближаясь к кристаллическому состоянию. Например, стекло по истечении нескольких сотен лет кристаллизуется. Процесс его кристаллизации может быть значительно ускорен при повышенной температуре, когда оно размягчается. В пластиках процесс кристаллизации сильно затруднён перепутыванием между собой образующих их длинных молекул. Для повышения качества пластиков специальной обработкой добываются того, чтобы практически все молекулы стали различными (физические длины, боковые цепи и т.д.), и для обеспечения стабильности нет необходимости иметь периодическую структуру.
Выбрав начало координат в некотором узле такой решетки, можно радиус-вектор любого другого узла представить в виде где n1, n2, n3 – целые числа (включая нуль). Векторы Конкретная кристаллическая решетка, вообще говоря, не может быть представлена в виде одной решетки Браве, а является совокупностью нескольких решеток Браве. Поэтому она называется сложной.
Как и следовало ожидать, площади элементарных ячеек в обоих случаях равны, хотя базисы различны. Все эти выводы без труда переносятся на трехмерный случай, в котором выбор элементарной кристаллической ячейки также неоднозначен, однако, объем элементарной ячейки при всевозможных выборах базиса является неизменным и по форме для объема параллелепипеда равным Это есть объем, приходящийся в решетке на один атом. Различные примитивные базисы отличаются друг от друга длиной базисных векторов или, что то же самое, основными периодами решетки. Примитивная решетка с минимальными периодами называется приведенной.
Рассмотрим в качестве примера плоскую решетку (рис. 4.6). Если в качестве базисных взять векторы На первый взгляд, кажется, что для учета этих узлов необходима ещё одна примитивная решетка, и, следовательно, исходная решетка является сложной, а не примитивной. Однако такое заключение неправильно. Возьмем в качестве базисных векторы a¢1 и a¢2. В этом базисе вся исходная решетка может быть представлена в виде одной примитивной решетки, т.е. исходная решетка тоже является примитивной. Это очевидно, если посмотреть на систему пунктирных линий (рис. 4.3). Трансляционная система. Ввиду бесконечной протяженности решетка обладает кроме симметрий, характерных для твердых тел, трансляционной симметрией, т.е. способностью совмещаться с собой в результате поступательного перемещения. Например, если примитивную решетку переместить вдоль одного из ребер элементарной ячейки на целое число основных периодов, то решетка совпадёт или совместится с собой. Если сместить решетку на вектор r, определенный в (4.1), то решетка опять совпадёт с собой. Поэтому вектор r называется вектором трансляции. Пользуясь этой терминологией, можно сказать, что вся примитивная решетка может быть получена из любого узла, если его подвергнуть всевозможным трансляциям параллельно базисным векторам. Пространственные группы. Элементы симметрии твердого тела образуют точечные группы симметрии. Если к ним добавить трансляционную симметрию, характерную для периодических бесконечных структур, то совокупность этих симметрий образует пространственную группу. Поэтому можно сказать, что кристаллические решетки характеризуются пространственными группами симметрии. Элементы симметрии решетки. Прежде всего необходимо отметить, что симметрии решетки в целом отличаются от симметрий её элементарной решетки. Это очевидно из того, что элементарная ячейка выбирается неоднозначно, а различные элементарные ячейки могут иметь различную симметрию. Поэтому под симметрией решетки понимается симметрия именно решетки, а не её элементарной ячейки.
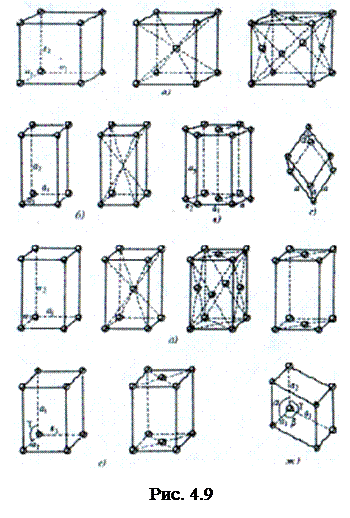
Рассмотрим атомы, лежащие в некоторой плоскости. Они создают плоскую кристаллическую решетку, узлы которой образуют систему правильных многоугольников, переходящих при вращении друг в друга и, следовательно, плотно, без промежутков, покрывающих всю поверхность. Рассмотрим точку О (рис. 4.7), в которой сходятся ребра примыкающих в этой точке правильных многоугольников. Если р – число ребер, сходящихся в этой точке, то угол между ребрами равен 2p/ р. С другой стороны, угол между сторонами правильного п -угольника равен p (п–2)/п. При заполнении плоскости правильными многоугольниками без промежутков эти углы равны: 2 p/ р= p (п–2)/п. (4.3) Отсюда следует, что р=2п/(п–2),(4.4) причем числа р и п должны быть целыми. Решениями этого уравнения в целых числах р и п являются значения п=3, п=4, п=6. (4.5) Таким образом, поверхность без промежутков можно покрыть равносторонними треугольниками, квадратами и правильными шестиугольниками (структура пчелиных сот)
Других правильных многоугольников, способных без промежутков покрыть поверхность, не существует. К ним добавляется, очевидно, возможная ось п=2, соответствующая отражению в плоскости, проходящей через ось, а также тривиальная ось п=1, соответствующая углу поворота на 2 p. Таким образом у кристаллической решетки возможны оси вращения только 2-, 3-, 4- и 6-го порядков. Аналогично показывается, что зеркально-поворотные оси могут быть только тех же порядков. В результате получается, что число элементов точечных групп симметрии у кристаллических решеток конечно, а следовательно, конечно и число возможных симметрий. Кристаллические классы. Поскольку сложная кристаллическая решетка состоит из решеток Браве, то классифицировать кристаллы в первую очередь целесообразно по симметрии решеток Браве, причем под симметрией, как это было только что сказано, понимается точечная симметрия. Такая классификация была произведена Браве. Он сказал, что хотя симметрия решетки не обязательно совпадает с симметрией любой примитивной ячейки, можно всегда найти такую примитивную ячейку, которая имеет те же элементы симметрии, что и решетка в целом. Это возможно для всех решеток, за исключением гексагональных, где примитивная ячейка не содержит всех элементов симметрии, которые имеются у решетки в целом. Наименьшая из примитивных ячеек, включающая в себя все элементы симметрии решетки, называется ячейкой или параллелепипедом Браве.
Таблица 4.1 Характеристики кристаллических систем
Симметрии сложных решеток. Поскольку сложная решетка слагается из примитивных, имеющих различные симметрии, то симметрия сложной решетки существенно отличается от симметрий слагающих её примитивных решеток. Кроме того, для сложной решетки возможны дополнительные элементы симметрии, а именно: винтовая ось и плоскость зеркального скольжения. Винтовой осью п -го порядка называется прямая, перемещение решетки вдоль которой с одновременным вращением на угол 2p¤ п приводит к её совпадению с собой. Винтовые оси одного и того же порядка могут отличаться друг от друга направлением вращения, т.е. быть «левыми» или «правыми». Плоскостью зеркального скольжения называется такая плоскость, при отражении в которой с одновременным смещением на определенное расстояние параллельно плоскости решетка совмещается сама с собой. Таким образом, наряду с элементами точечной симметрии и трансляционной симметрией решетка обладает другими элементами симметрии - винтовыми осями и плоскостями зеркального скольжения. Совокупность всех элементов симметрии называется её пространственной группой. Как было показано Е.С. Фёдоровым, всего может существовать 230 пространственных групп. Эти группы называются группами Фёдорова или фёдоровскими группами. Не все они обнаружены у кристаллов, имеющихся в природе. Найдены пока кристаллы для 177 фёдоровских групп. Более подробно эти вопросы рассматриваются в курсе кристаллографии. Кристаллографические системы координат. В качестве систем координат, в которых задается положение атомов решетки, берут прямолинейные системы координат, оси которых совпадают с ребрами параллелепипеда Браве, а начало находится в одном из узлов кристаллической решетки. В качестве единицы длины по каждой оси принимается длина соответствующего ребра параллелепипеда Браве. Поэтому координаты атомов выражаются целыми числами. Такие системы координат называются кристаллографическими. Выбор осей координат дается в табл. 4.1. В кубических, тетрагональных и ромбических кристаллах системы координат являются прямоугольными, остальные – косоугольными. В гексагональных кристаллах за оси X и Y параллелепипеда Браве принимаются стороны основания правильного шестиугольника (см. рис. 4.9), составляющие угол 120°друг с другом, а ось Z направлена перпендикулярно основанию. Выбор параллелепипеда Браве для моноклинных и триклинных кристаллов не однозначен. Условились, что в моноклинных кристаллах за ось Z берется та, которая образует прямой угол с двумя другими осями (см. табл. 4.1).
Уравнение любой плоскости в прямолинейных (но не обязательно прямоугольных!) координатах имеет вид:
где |ΟΑ|, |ОΒ|, |ΟС| - длины отрезков (в осевых единицах), отсекаемых плоскостью на осях координат (рис. 4.11). Если в точке пересечения оси с плоскостью находится атом, то соответствующая из величин А, В, С является целочисленной. Но, вообще говоря, атомная плоскость может пересекаться с осями координат также и в точках, в которых нет атомов. В этом случае соответствующая из величин |ΟΑ|, |ОΒ|, |ΟС| не будет целочисленной. Однако она всегда выражается рациональным числом (положительным или отрицательным). Чтобы в этом убедиться, достаточно заметить, что для атомов, находящихся в рассматриваемой плоскости, величины x, y, z в уравнении (4.6) являются целочисленными. Поэтому, взяв каких-то три конкретных атома в плоскостях, не лежащих на одной прямой, мы из (4.6) получим три линейных уравнения с целочисленными коэффициентами для определения трех неизвестных (1/|ΟΑ|, 1/|ОΒ|, 1/|ΟС|). Ясно, что решение этих уравнений дается рациональными числами, а следовательно, и величины |ΟΑ|, |ОΒ|, |ΟС| являются рациональными числами. Поэтому уравнение (4.6) может быть переписано в виде
где h, k, l – целые числа, причем можно считать, что они не имеют общего множителя, поскольку в противном случае на этот общий множитель можно было бы сократить все члены уравнения. Целые числа h, k, l однозначно определяют положение плоскости. Они называются миллеровскими числами и записываются в виде последовательности чисел, заключенной в скобки: (h k l). Если индекс отрицательный, то знак минус ставится над соответствующим числом, например, ( Обозначение направлений. Направление, перпендикулярное плоскости, характеризуемой миллеровскими индексами (h k l), обозначается теми же числами, но заключенными в квадратные скобки [ h k l ].
|

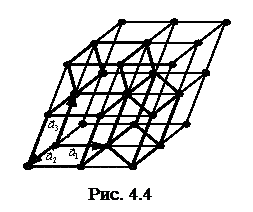 Примитивная решетка. В результате периодичности структуры кристаллической решетки должна существовать некоторая элементарная совокупность атомов, повторением которой во всех направлениях можно исчерпать всю не ограниченную в пространстве решетку. Как элементарная совокупность атомов (для простоты выражений мы говорим об атомах, хотя это могут быть и молекулы, ионы), так и порождаемая её повторением решетка, являются, вообще говоря, очень сложными образованиями. Поэтому всю решетку целесообразно разбить на некоторые, более простые подрешетки, каждая из которых была бы достаточно простой. Ясно, что эта подрешетка сама является решеткой. Наиболее простой решеткой является решетка, состоящая из параллелепипедов как элементарной совокупности атомов, повторением которой исчерпывается вся решетка (рис. 4.4 ).
Примитивная решетка. В результате периодичности структуры кристаллической решетки должна существовать некоторая элементарная совокупность атомов, повторением которой во всех направлениях можно исчерпать всю не ограниченную в пространстве решетку. Как элементарная совокупность атомов (для простоты выражений мы говорим об атомах, хотя это могут быть и молекулы, ионы), так и порождаемая её повторением решетка, являются, вообще говоря, очень сложными образованиями. Поэтому всю решетку целесообразно разбить на некоторые, более простые подрешетки, каждая из которых была бы достаточно простой. Ясно, что эта подрешетка сама является решеткой. Наиболее простой решеткой является решетка, состоящая из параллелепипедов как элементарной совокупности атомов, повторением которой исчерпывается вся решетка (рис. 4.4 ).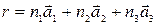 , (4.1)
, (4.1)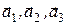 называются базисными, а их совокупность – базисом решетки. Длины ребер
называются базисными, а их совокупность – базисом решетки. Длины ребер 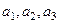 называются основными периодами решетки. Параллелепипед с ребрами
называются основными периодами решетки. Параллелепипед с ребрами 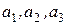 вместе с атомами в его вершинах называется элементарной ячейкой кристаллической решетки. Если в формуле (4.1) числа n1, n2, n3 пробегают всевозможные независимые целочисленные значения от -¥; до +¥;, то радиус-вектор r проходит все узлы решетки и нет никаких узлов решетки, которые не охватывались бы формулой (4.1). Такая решетка называется примитивной или решеткой Браве, а её элементарная ячейка – примитивной ячейкой.
вместе с атомами в его вершинах называется элементарной ячейкой кристаллической решетки. Если в формуле (4.1) числа n1, n2, n3 пробегают всевозможные независимые целочисленные значения от -¥; до +¥;, то радиус-вектор r проходит все узлы решетки и нет никаких узлов решетки, которые не охватывались бы формулой (4.1). Такая решетка называется примитивной или решеткой Браве, а её элементарная ячейка – примитивной ячейкой.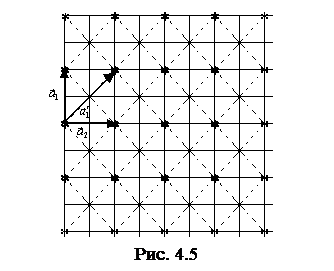 Неоднозначность выбора базиса примитивной решетки. Выбор базиса даже примитивной решетки не является однозначным. В этом легко убедиться по рис. 4.5, где для двумерного случая параллельными пунктирными линиями показаны два возможных построения примитивной решетки с различными базисами. В первом случае базис составлен векторами
Неоднозначность выбора базиса примитивной решетки. Выбор базиса даже примитивной решетки не является однозначным. В этом легко убедиться по рис. 4.5, где для двумерного случая параллельными пунктирными линиями показаны два возможных построения примитивной решетки с различными базисами. В первом случае базис составлен векторами 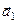 и
и  , во втором – векторами
, во втором – векторами 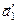 ,
, 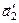 . Элементарная ячейка в первом случае является прямоугольным параллелограммом, во втором – непрямоугольным. Около каждого атома в узле решетки в плоском случае располагаются четыре элементарных ячейки. Следовательно, площадь, занимаемая одним атомом в решетке, равная общей площади, деленной на число атомов, равна площади элементарной ячейки
. Элементарная ячейка в первом случае является прямоугольным параллелограммом, во втором – непрямоугольным. Около каждого атома в узле решетки в плоском случае располагаются четыре элементарных ячейки. Следовательно, площадь, занимаемая одним атомом в решетке, равная общей площади, деленной на число атомов, равна площади элементарной ячейки 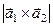 в первом случае и
в первом случае и 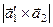 - во втором.
- во втором.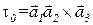 . (4.2)
. (4.2)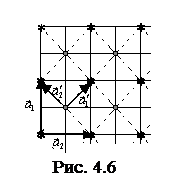 Определить, является некоторая заданная решетка примитивной или сложной, не всегда легко с первого взгляда. Лучше всего это делать, рассматривая всю решетку, а не её небольшую часть, равную элементарной ячейке. Задача сводится к возможности проведения трех систем параллельных плоскостей таким образом, чтобы все атомы решетки оказались в точках пересечения плоскостей и не было бы атомов, не попавших в эти точки пересечения плоскостей.
Определить, является некоторая заданная решетка примитивной или сложной, не всегда легко с первого взгляда. Лучше всего это делать, рассматривая всю решетку, а не её небольшую часть, равную элементарной ячейке. Задача сводится к возможности проведения трех систем параллельных плоскостей таким образом, чтобы все атомы решетки оказались в точках пересечения плоскостей и не было бы атомов, не попавших в эти точки пересечения плоскостей.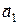 ,
, 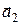 , то решетка представляется сложной, поскольку атомы, находящиеся в центрах квадратов, не попадают в узлы примитивной решетки, построенной на этом базисе.
, то решетка представляется сложной, поскольку атомы, находящиеся в центрах квадратов, не попадают в узлы примитивной решетки, построенной на этом базисе.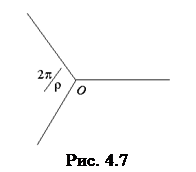 Ясно, что всякая примитивная решетка имеет центр симметрии, которым может быть любой узел примитивного параллелепипеда, середина его ребер и центры его граней. Плоскость симметрии также является элементом симметрии решеток. Что же касается осей, то они могут быть лишь осями 2-, 3-, 4- и 6-го периодов, а оси других порядков невозможны. Для доказательства заметим, что при вращении атомы решетки перемещаются в плоскостях, перпендикулярных оси вращения.
Ясно, что всякая примитивная решетка имеет центр симметрии, которым может быть любой узел примитивного параллелепипеда, середина его ребер и центры его граней. Плоскость симметрии также является элементом симметрии решеток. Что же касается осей, то они могут быть лишь осями 2-, 3-, 4- и 6-го периодов, а оси других порядков невозможны. Для доказательства заметим, что при вращении атомы решетки перемещаются в плоскостях, перпендикулярных оси вращения.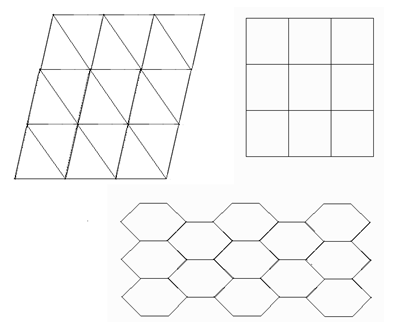
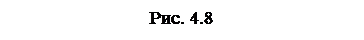
 Имеется шесть типов примитивных параллелепипедов Браве, и поэтому с учетом гексагональной решетки – всего семь типов решеток или семь типов кристаллических систем. Помещение в центрах граней или в центре объёма параллелепипедов Браве новых атомов не изменяет симметрии решетки, но добавляет новые типы решетки. Поэтому всего существует 14 типов решеток Браве, распределенных по семи кристаллическим системам. Подробное описание этих решеток является предметом кристаллографии, а мы здесь ограничимся лишь краткими замечаниями. На рис. 4.9 изображены решетки, принадлежащие семи кристаллическим системам. В каждой из систем, за исключением гексагональной, первым
Имеется шесть типов примитивных параллелепипедов Браве, и поэтому с учетом гексагональной решетки – всего семь типов решеток или семь типов кристаллических систем. Помещение в центрах граней или в центре объёма параллелепипедов Браве новых атомов не изменяет симметрии решетки, но добавляет новые типы решетки. Поэтому всего существует 14 типов решеток Браве, распределенных по семи кристаллическим системам. Подробное описание этих решеток является предметом кристаллографии, а мы здесь ограничимся лишь краткими замечаниями. На рис. 4.9 изображены решетки, принадлежащие семи кристаллическим системам. В каждой из систем, за исключением гексагональной, первым 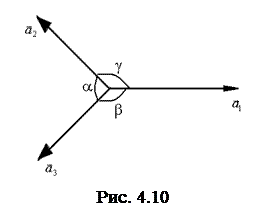 показан основной параллелепипед Браве, а затем указаны решетки, которые получаются центрированием объема и граней основного параллелепипеда. Эта операция не изменяет симметрии решетки, но, конечно, примитивные ячейки получаемой в результате этого решетки уже не совпадают с основным параллелепипедом Браве и имеют симметрии, отличные от симметрии решетки. Что касается гексагональной системы, то у неё элементарная ячейка, имеющая те же элементы симметрии, что и решетка, не является параллелепипедом. Элементарный параллелепипед в этом случае указан на рисунке вместе с элементарной ячейкой. На рис. 4.10 даны обозначения осей и углов основного параллелепипеда Браве различных кристаллических систем, характеристика которых дана в табл. 4.1.
показан основной параллелепипед Браве, а затем указаны решетки, которые получаются центрированием объема и граней основного параллелепипеда. Эта операция не изменяет симметрии решетки, но, конечно, примитивные ячейки получаемой в результате этого решетки уже не совпадают с основным параллелепипедом Браве и имеют симметрии, отличные от симметрии решетки. Что касается гексагональной системы, то у неё элементарная ячейка, имеющая те же элементы симметрии, что и решетка, не является параллелепипедом. Элементарный параллелепипед в этом случае указан на рисунке вместе с элементарной ячейкой. На рис. 4.10 даны обозначения осей и углов основного параллелепипеда Браве различных кристаллических систем, характеристика которых дана в табл. 4.1.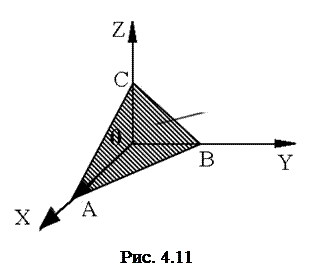 Обозначение атомных плоскостей. В бесконечном кристалле можно провести бесконечное число плоскостей, в каждой из которых лежит бесконечное число атомов. Для того чтобы характеризовать семейство параллельных плоскостей, достаточно определить одну из них, причем без потери общности можно ограничиться примитивными решетками.
Обозначение атомных плоскостей. В бесконечном кристалле можно провести бесконечное число плоскостей, в каждой из которых лежит бесконечное число атомов. Для того чтобы характеризовать семейство параллельных плоскостей, достаточно определить одну из них, причем без потери общности можно ограничиться примитивными решетками.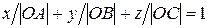 , (4.6)
, (4.6)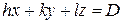 , (4.7)
, (4.7)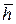
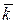
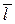 ).
).


