МОДЕЛИРОВАНИЕ СИСТЕМЫ УПРАВЛЕНИЯ ДВИЖЕНИЕМ.
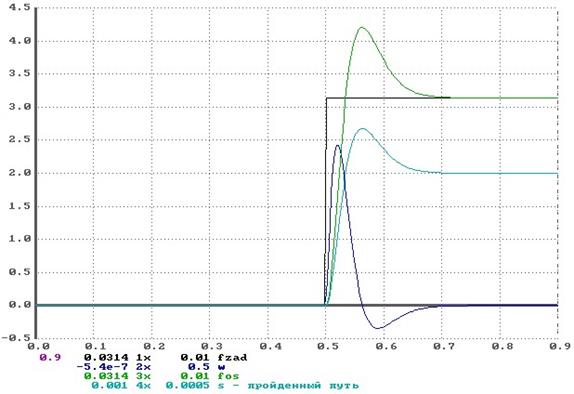
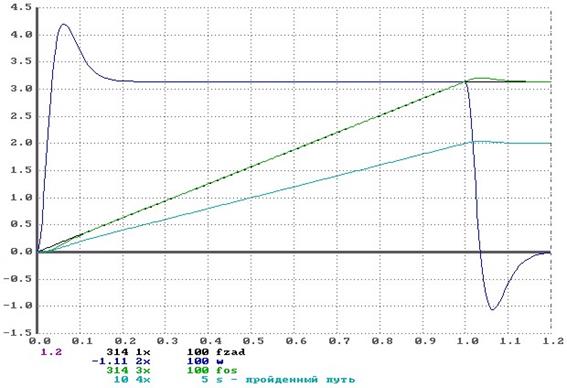
В соответствии со структурной схемой приведенной на рисунке 8.1 с учетом особенностей построения импульсно-фазового СЭП (рисунок 6.4) составлена математическая модель следящего электропривода для моделирования в системе АЛМИК. Тексты модели представлены в приложении А. В соответствии со структурной схемой был смоделирован процесс «в малом» отработки единичного воздействия (без учета компенсации скоростной ошибки и дискретности задания управляющего воздействия). График представлен на рисунке 8.2. Из рисунка видно, что характер переходного процесса монотонный, без перерегулирования, время переходного процесса (время вхождения выходной величины в 5%-ю зону) составляет tпп = 0,123 с, что соответствует выбранной настройке. На рисунках 8.3 и 8.4 представлены графики отработки одного и пяти импульсов. Как видно из графиков, пройденный путь в первом случае равен 0,001мм, что соответствует одной дискрете, в другом 0.005 мм, что в 5 раз больше чем, величина дискреты, следовательно, число импульсов на входе СУД отвечает за перемещение рабочего органа, на заданное количество дискрет. Рассмотрим переходный процесс в режиме равномерной заводки, для номинальной скорости Для устранения скоростной ошибки введем канал компенсации скоростной ошибки. На рисунке 8.6 и 8.7 представлены переходные процессы при отработке 1 и 10 импульсов. Из рисунка 8.6 видно, появляется перерегулирование по пути, что вызвано форсировкой скорости привода, поступающей по каналу компенсации. То же можно увидеть на рисунке 8.7, при отработке приводом 10 дискрет в шаговом режиме. Рассмотрим процесс равномерной заводки, при отработке приводом 10000 дискрет на номинальной скорости
рис. 8.1. Модель автономного СЭП импульсно-фазового типа.
рис. 8.2. Отработка одного импульса задания в непрерывной системе.
рис. 8.3. Отработка одного импульса задания, с учётом дискретности управления.
рис. 8.4. Отработка пяти импульсов задания без канала компенсации скоростной ошибки.
рис. 8.5. Отработка максимального числа импульсов задания без канала компенсации скоростной ошибки.
рис. 8.6. Отработка одного импульса задания, с каналом компенсации скоростной ошибки.
рис. 8.7. Отработка десяти импульсов задания, с каналом компенсации скоростной ошибки.
рис. 8.8. Отработка максимального числа импульсов задания с каналом компенсации скоростной ошибки.
8.1 ИССЛЕДОВАНИЕ КОНТУРНОЙ ОШИБКИ ПРИ ЛИНЕЙНОЙ ИНТЕРПОЛЯЦИИ.
При исследовании контурной ошибки не будем учитывать нелинейности привода (ограничения по скорости и т.д.). Контурная ошибка при линейной интерполяции определяется выражением:
где
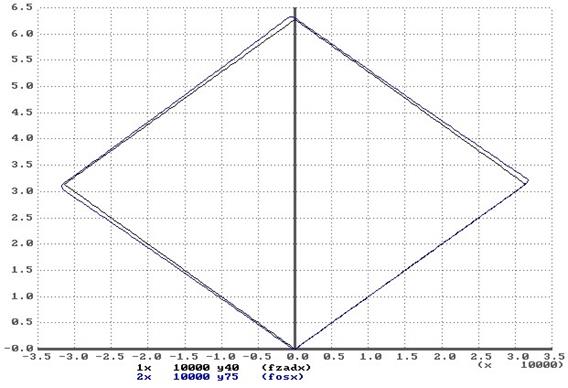
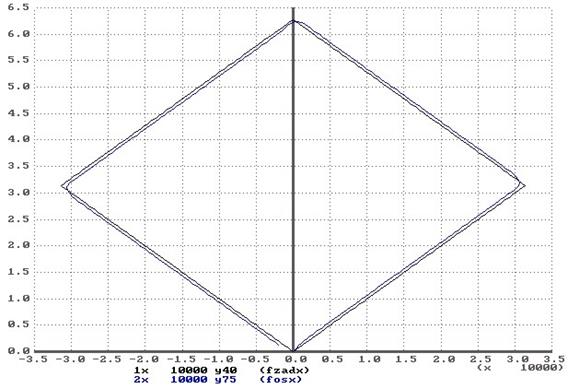
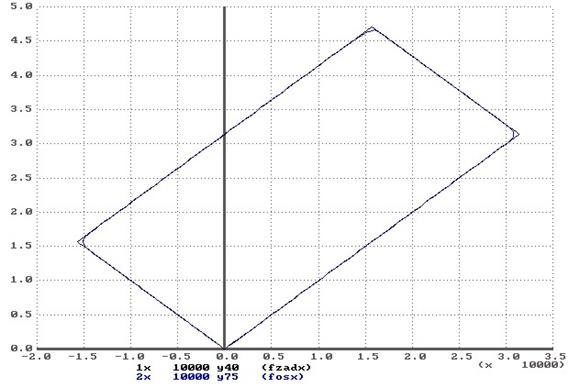
При угле На рисунке 8.9 представлена фазовая траектория привода при отработке траектории в виде квадрата со стороной равной 10000 дискретам, с равными добротностями по обеим координатам X и Y. Из графиках видно, что контурной ошибки нет, привод в точности отрабатывает ту траекторию, которую ему задали. Рассмотрим теперь процесс отработки данной траектории приводами с разными добротностями, например привод по координате Y будет иметь добротность на 25% меньшую, чем добротность по координате X, тогда рассмотрим следующую фазовую траекторию, представленную на рисунке 8.10. Имеет место контурная ошибка, т.е. действительная траектория отличается от заданной. Отработки траектории прямоугольника со сторонами 10000 и 5000 дискрет представлены на рисунках 8.11 и 8.12. На рисунке 8.11 привод отрабатывает траекторию с одинаковой добротностью по обеим координатам, и видим, что действительная траектория совпадает с заданной - контурная ошибка равна нулю. Так как по координате X привод отрабатывает 5000 дискрет, а по Y - 10000, то работа приводов идет на На рисунке 8.13 представлена фазовая траектория при увеличенных в полтора раза добротностях по обеим координатам. Как видно из рисунка, траектории заданная и действительная полностью совпадают, даже на этапах разгона и реверса и торможения координатных приводов. Если же дальше увеличивать добротность, это может привести к неудовлетворительной траектории, что видно из рисунка 8.14. Рассмотрим теперь работу привода с каналом компенсацией скоростной ошибки. На рисунках 8.15 и 8.16 представлены фазовые траектории отработки заданной траектории в виде квадрата со стороной 10000 дискрет для случаев равенства и неравенства добротностей приводов координат X и Y. В первом случае, как видно из графика, привод в точности отрабатывает заданную траекторию, и лишь незначительные путевые перерегулирования искажают траекторию. Во втором случае, также траектория Из всего выше сказанного можно сделать вывод, что для реализации режима линейной интерполяции при нулевой контурной ошибке необходимо обеспечить равенство добротностей координатных приводов. Если же нет возможности уровнять добротности, то необходимо предусмотреть в приводах канал компенсации скоростной ошибки, тогда даже при больших отличиях добротностей, траектория будет отработана достаточно точно.
рис. 8.9. Фазовая траектория 2-х координатного привода при линейной интерполяции с
рис. 8.10. Фазовая траектория 2-х координатного привода при линейной интерполяции с
рис. 8.11. Фазовая траектория 2-х координатного привода при линейной интерполяции с
рис. 8.12. Фазовая траектория 2-х координатного привода при линейной интерполяции с
рис. 8.13. Фазовая траектория 2-х координатного привода при линейной интерполяции с
рис. 8.14. Фазовая траектория 2-х координатного привода при линейной интерполяции с
рис. 8.15. Фазовая траектория 2-х координатного привода при линейной интерполяции с каналом компенсации скоростной ошибки при
рис. 8.16. Фазовая траектория 2-х координатного привода при линейной интерполяции с каналом компенсации скоростной ошибки при
рис. 8.17. Фазовая траектория 2-х координатного привода при линейной интерполяции с каналом компенсации скоростной ошибки при
|

 =314 рад/с, для этого необходимо подать на вход СУД 10000 импульсов (
=314 рад/с, для этого необходимо подать на вход СУД 10000 импульсов (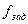 = 10000Гц). Переходный процесс представлен на рисунке 8.5. Как видно, имеет место скоростная ошибка
= 10000Гц). Переходный процесс представлен на рисунке 8.5. Как видно, имеет место скоростная ошибка  = 20 рад. Скорость установилась на уровне
= 20 рад. Скорость установилась на уровне 
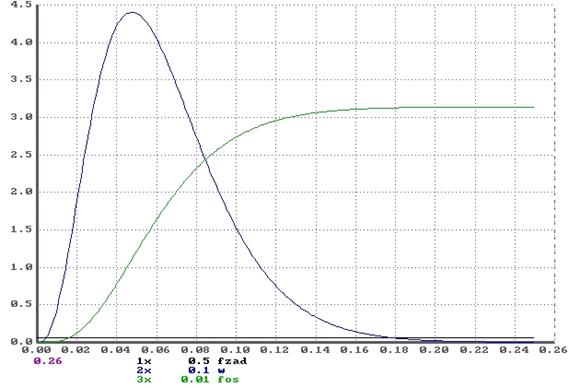




 (7.1)
(7.1) - контурная скорость привода;
- контурная скорость привода; - добротности приводов по координатам X и Y.
- добротности приводов по координатам X и Y. (угол между координатой и траекторией кривой) равном 45 градусам, контурная ошибка максимальна, следовательно, исследуем ее на примере отработки приводами квадратной траектории.
(угол между координатой и траекторией кривой) равном 45 градусам, контурная ошибка максимальна, следовательно, исследуем ее на примере отработки приводами квадратной траектории.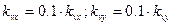 . Из нее видно, что даже при таких добротностях траектория отрабатывается достаточно точно, имеет место лишь динамическая ошибка при разгоне приводов.
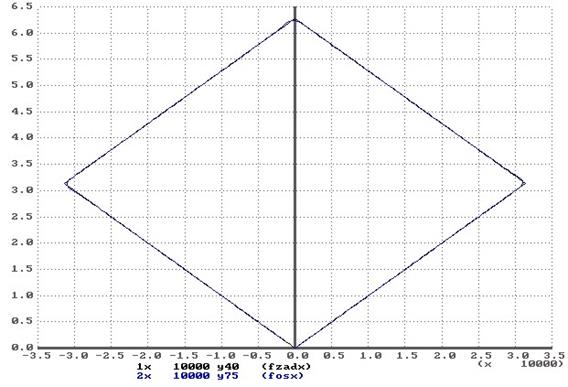
. Из нее видно, что даже при таких добротностях траектория отрабатывается достаточно точно, имеет место лишь динамическая ошибка при разгоне приводов.
 .
.
 .
.

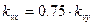 .
.
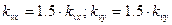 .
.
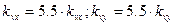 .
.