Капиллярные явления в насыщенных пористых средах.
Явление поверхностного натяжения приводит не только к искривлению поверхности раздела фаз на границе "жидкость – газ" или на границе двух несмешивающихся жидкостей, но проявляется в виде капиллярных сил, если эти системы находятся в ограниченном пространстве тонких трубок или капилляров. Как известно, на искривленной поверхности двух фаз давление претерпевает скачок (давление внутри капли жидкости или газа всегда больше, чем снаружи). Разность внутреннего и внешнего давлений на искривленной поверхности называется капиллярным давлением и всегда направлено внутрь жидкости в системе "жидкость – газ" или под вогнутую поверхность в системе "жидкость-жидкость" (рис. 2.4.12).
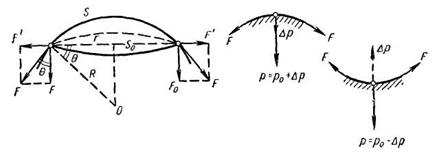
Рис.2.4.12. Капиллярное давление на искривленной поверхности раздела фаз. Как видно из рисунка 2.4.12, в зависимости от выпуклости или вогнутости поверхности, дополнительное давление, создаваемое силами поверхностного натяжения давление может либо прибавляться к первоначальному давлению (в случае плоской поверхности), либо отниматься от него. При этом поверхность жидкость может быть и не сферической. Поэтому в общем случае выберем на поверхности участок, ограниченный бесконечно малым прямоугольником (рис. 2.4.13.)
Рис.2.4.13. Графическое пояснение формулы Лапласа. Исходя из определения поверхностного натяжения и рис. 2.4.13, можно показать, что дополнительное капиллярное давление определяется выражением, известным как формула Лапласа:
где R1 и R2 – радиусы кривизны двух взаимно перпендикулярных нормальных сечений к поверхности жидкости (на рис.2.4.13: R1 -радиус кривизны дуги АВ, R2 - радиус кривизны дуги AD); знак в правой части означает выпуклость или вогнутость поверхности. В случае сферической поверхности получим:
если поверхность плоская:
где Одним из проявлений капиллярных сил является поднятие или опускание столбика жидкости в капилляре в зависимости от порядка смачивания его стенок (рис.2.4.14).
Рис.2.4.14. Действие капиллярных сил в вертикальных капиллярах. Высота поднятия (опускания) жидкости в сферическом капилляре со смачивающимися (не смачивающимися) ею стенками определяется соотношением:
и равна:
В пористой среде аналогичным образом происходит процесс капиллярной пропитки смачивающей фазой. Скорость пропитки можно рассчитать по формуле:
где μ; – вязкость жидкости, t – время пропитки. В случае избирательного смачивания в горизонтальном капилляре, и если смачивающая жидкость вытесняет несмачивающую, скорость пропитки можно найти из уравнения:
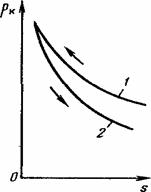
где l0 – общая длина пористой среды; Итак, если пористая среда первоначально заполнена несмачивающей фазой, а затем заполняется смачивающей - это пропитка; если же первоначально пористая среда насыщена смачивающей фазой, которая замещается несмачивающей – это процесс вытеснения. В обоих случаях капиллярное давление будет меняться по мере изменения соотношения фаз. На рис. 2.4.15 показано изменение капиллярного давления в двух рассматриваемых процессах – вытеснения (1) и пропитки (2). Причем эти кривые, как правило, не совпадают. Это явление называется капиллярным гистерезисом.
Пусть гидрофобная поверхность, насыщенная нефтью (тогда s на рис. 2.4.15 относится к нефти), заполняется водой (вытеснение). В процессе пропитки (кривая 2) нефть заполнит самые мелкие поры (в которых капиллярное давление максимально), а вода – крупные, и общее капиллярное давление будет уменьшаться. При обратном процессе – вытеснении нефти водой, последняя постепенно будет заполнять поры, занятые нефтью (сначала, разумеется, более крупные), уменьшая ее насыщенность (по стрелке на кривой 1). Таким образом, количество пор, занятых двухфазной системой, будет больше, и капиллярное давление системы – увеличится. Однако самые мелкие поры, а главное, поры, имеющие узкие перемычки, останутся насыщенными нефтью. Это и приводит к появлению капиллярного гистерезиса.
|


 , (2.4.6)
, (2.4.6)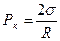 , (2.4.7)
, (2.4.7) , (2.4.8)
, (2.4.8)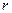 - радиус капилляра.
- радиус капилляра.


 . (2.4.9)
. (2.4.9)