Работа адгезии и теплота смачивания
При взаимодействии жидких и твердых тел важное значение имеют еще две определяемые характеристики: работа адгезии и теплота смачивания. Работа адгезии (прилипания) – это работа, необходимая для отрыва жидкости от твердой поверхности в направлении, перпендикулярном к границе раздела, и отнесенная к единице площади поверхности. Единица измерения работы адгезии - [Дж/м2] или [эрг/см2]. Известна также работа когезии (слипания),которая определяет аналогичным образом разрыв однородной фазы. Работа адгезии для рассмотренной схемы можно записать в виде уравнения:
Уравнение (2.4.3) называется уравнением Дюпрe. Если учесть уравнение Юнга (2.4.1), получим:
Или для системы «вода – нефть»:
Уравнение (2.4.4) называется уравнением Дюпре – Юнга. Если жидкость полностью не смачивает твердую поверхность, т. е. q = 1800 и cosq = -1, то Wа = 0 (что с формальной точки зрения справедливо: нет смачивания – не требуется совершения работы, хотя с физической точки зрения в реальном ограниченном пространстве пор среды условие невыполнимо, т.к. межмолекулярное взаимодействие двух сред при их контакте всегда имеется, и Wа > 0 в любом случае). Если имеет место полное смачивание, т.е. q = 00 и cosq=1, тогда Wк = 2sвн – эта работа, необходимая для образования двух жидких поверхностей, следовательно, при полном смачивании жидкость отрывается не от поверхности, а происходит разрыв самой жидкости (работа когезии). Подставляя в уравнение (2.4.4) выражение для работы когезии, получим:
Полученное выражение позволяет оценить степень смачивания твердой поверхности жидкостью в зависимости от соотношения сил межмолекулярного взаимодействия внутри жидкости (работа когезии) и способности ее взаимодействия с твердой поверхностью (работа адгезии). Так, например, непременным условием смачивания, т.е. cosθ > 0, будет С другой стороны, в уравнения (2.4.5) входят слагаемые, вполне поддающиеся экспериментальному определению, что также делает их весьма полезными.
|

 (2.4.3)
(2.4.3) ,
, . (2.4.4)
. (2.4.4) или
или 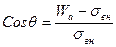 . (2.4.5)
. (2.4.5)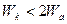 .
.


