Теорема о смещении аргумента
Если то
Проведя z -преобразование с уравнением (20) получим:
Из (22) согласно 2-му определению передаточной функции, как отношение изображения выходного сигнала ко входному, получим передаточную функцию фильтра:
Существуют цифровые фильтры, в которых выходной сигнал формируется только по выборке входного сигнала. Уравнение их работы выглядит:
Если с (25) провести дискретное z -преобразование, то с учетом теории о смещении аргумента получим:
Такой фильтр имеет полюс z = 0 кратности Оказывается, передаточную функцию (23) можно записать в форме (26), но с бесконечным верхним пределом:
где (V) называется рекурсивным соотношением, когда величина выражается через обращение к своим предыдущим значениям. В соответствии с рекурсивным соотношением цифровые фильтры, описываемые математическими зависимостями: (19), (20), (22), (23), (27), называются рекурсивными, а также фильтрами с бесконечной памятью из-за верхнего предела (27) – “ Цифровые фильтры описываемые (25) и (26) называются нерекурсивными, трансверсальными, а также фильтрами с конечной памятью.
|

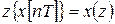 ,
,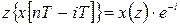

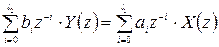 (22)
(22)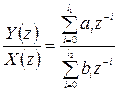 (23)
(23)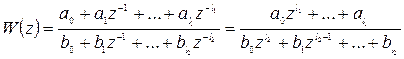 (24)
(24)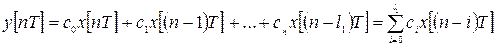 (25)
(25)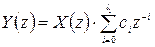
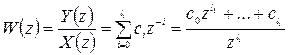 (26)
(26)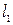 и нули числителя.
и нули числителя.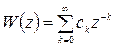 , (27)
, (27)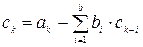 (V)
(V) ”.
”.


