Интерполяционный многочлен Лагранжа
Формула (7) в точности описывает табличные значения. А в промежутках между дискретными отсчетами возникает погрешность, которая оценивается остаточным членом интерполяционного ряда Ньютона, выражающегося следующим образом:
Преобразуем формулу (9) следующим образом: пусть во временном интервале
Тогда:
………………………………..
В итоге (9) преобразуется:
А также потребуем, чтобы максимальная погрешность была не больше допускаемой:
Частота дискретизации:
Пример. Линейная аппроксимация (отрезками с постоянным наклоном).
При ступенчатой аппроксимации n = 0.
|

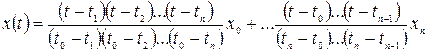 (7)
(7) (8)
(8) (9)
(9)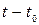 укладывается число квантов
укладывается число квантов 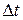 равное
равное  :
:
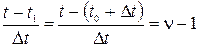
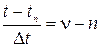
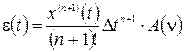 (10)
(10)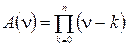 (11)
(11)
 (12)
(12)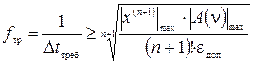 (13)
(13)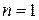

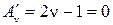
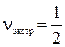
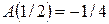
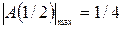
 (14)
(14)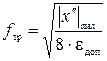
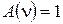
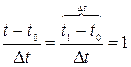
 (15)
(15)


