Построение ортогонального и аксонометрического чертежей правильной шестиугольной пирамиды
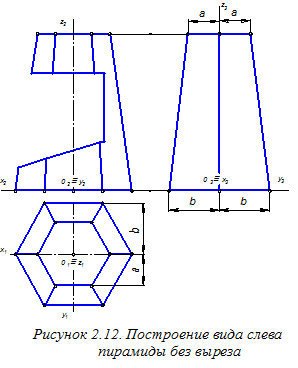
Для построения видов сверху и слева, а также аксонометрического изображения данной пирамиды осуществим привязку этой фигуры к прямоугольной системе координат Оxyz (рисунок 2.12). В качестве горизонтальной координатной плоскости выберем плоскость нижнего основания пирамиды. Сначала выполним построение вида слева пирамиды, не содержащей выреза (см. рисунок 2.12). Для этого построим профильные проекции вершин верхнего и нижнего оснований пирамиды и соединим их между собой. Для построения некоторых из этих вершин используем перенос их ординат с вида сверху на вид слева (см. отрезки а и b на рисунке 2.12). Точки граничных линий выреза, расположенные на боковых рёбрах пирамиды, строим на виде сверху по линиям связи на горизонтальных проекциях соответствующих рёбер (рисунок 2.13).Точки граничных линий выреза, расположенные на боковых гранях пирамиды, например точки 1 и 1, строим с помощью вспомогательной горизонтальной плоскости a¢;. Такая плоскость пересекает боковую поверхность пирамиды по правильному шестиугольнику, одна из вершин которого (точка М) принадлежит правому боковому ребру пирамиды (см. проекции М2 и М1 на рисунке 2.13).
Построение на виде слева точек граничных линий выреза, расположенных на боковых рёбрах пирамиды, осуществляем по линиям связи на профильных проекциях соответствующих рёбер, а точек 1(1) и 2(2), расположенных на боковых гранях пирамиды, строим переносом ординат m и n этих точек с вида сверху на вид слева (см. соответствующие размеры на рисунке 2. 13). Для завершения построений видов сверху и слева последовательно соединяем найденные точки, удаляем лишние участки боковых рёбер пирамиды и показываем невидимые участки линий чертежа. Окончательное оформление ортогонального чертежа сводится к обводке его изображений линиями, соответствующими ГОСТ 2.303-68 [1], нанесению необходимых Далее выполняем построение аксонометрической проекции рассматриваемой пирамиды с учётом привязки её к прямоугольной системе координат Охуz (см. рисунок 2.13). На отдельном листе формата А3 или А4 строим аксонометрические оси (см. рисунок 2.4) и правильный шестиугольник - нижнее основание пирамиды (см. рисунок 2.5). При этом длины обозначенных отрезков измеряем на ортогональном чертеже пирамиды и откладываем на аксонометрическом чертеже по координатным осям или на отрезках, параллельных этим осям. Из центра основания – точки О¢;, вверх, по оси О¢z¢; откладываем высоту h пирамиды и получаем центр верхнего основания пирамиды – точку О ¢; (рисунок 2. 14). Строим аксонометрию верхнего основания пирамиды аналогично нижнему основанию, используя его ортогональные изображения.
 Соединяя соответствующие вершины верхнего и нижнего оснований пирамиды, строим её изображение, не содержащее выреза. Далее необходимо построить вырез. Для этого сначала изобразим его фронтальную вторичную проекцию - ломаную 42¢- 12¢-22¢- 32¢ (рисунок 2.15), используя размеры a, b, c, d, e, перенося их с главного вида ортогонального чертежа (см. Соединяя соответствующие вершины верхнего и нижнего оснований пирамиды, строим её изображение, не содержащее выреза. Далее необходимо построить вырез. Для этого сначала изобразим его фронтальную вторичную проекцию - ломаную 42¢- 12¢-22¢- 32¢ (рисунок 2.15), используя размеры a, b, c, d, e, перенося их с главного вида ортогонального чертежа (см.
соответствующие размеры на рисунке 2. 13) на аксонометрический чертёж параллельно соответствующим координатным осям. Построенная вторичная проекция выреза условно показана утолщённой линией. Далее на указанной ломаной необходимо найти фронтальные вторичные проекции точек, принадлежащих граничным линиям выреза и расположенным на боковых рёбрах пирамиды. Для этого сначала на оси О¢х¢ строим вторичные фронтальные проекции вершин нижнего основания пирамиды (рисунок 2.16). Последовательность построения показана стрелками, а сами проекции показаны точками. Здесь же приведены аналогичные построения для вершин верхнего основания пирамиды. Соединяя соответствующие точки нижнего и верхнего оснований пирамиды, строим фронтальные вторичные проекции боковых рёбер пирамиды (рисунок 2. 17) и на них находим искомые вторичные проекции точек. Эти проекции помечены стрелками. Через найденные точки проводим прямые, параллельные оси О¢у¢;, до пересечения с соответствующими рёбрами (рисунок 2.18). Направление этих прямых показано стрелками. Найденные точки принадлежат граничным линиям выреза на пирамиде.
пирамиды (см. рисунок 2.13). Последовательно соединяя построенные точки, принадлежащие граничным линиям выреза, и удаляя ненужные отрезки боковых рёбер, получаем окончательный аксонометрический чертёж рассматриваемой пирамиды (рисунок 2.19).
|

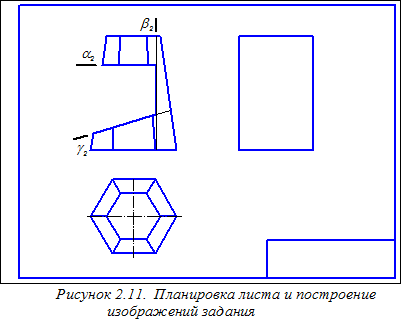 Планировка листа и построение изображений чертежа по размерам, нанесённым на эти изображения в индивидуальном задании, показаны на рисунке 2.11. Изображения включают в себя главный вид, частично вид сверху и габаритный прямоугольник для дальнейшего построения вида слева. Рассматриваемая правильная шестиугольная пирамида имеет вырез, образованный тремя плоскостями: горизонтальной (a), профильной (b) и фронтально проецирующей (g). На виде сверху отсутствует изображение линий пересечения плоскостей a и b, b и g, определяющих границы выреза, а также линии пересечения этих плоскостей с боковыми гранями пирамиды (граничные линии выреза).
Планировка листа и построение изображений чертежа по размерам, нанесённым на эти изображения в индивидуальном задании, показаны на рисунке 2.11. Изображения включают в себя главный вид, частично вид сверху и габаритный прямоугольник для дальнейшего построения вида слева. Рассматриваемая правильная шестиугольная пирамида имеет вырез, образованный тремя плоскостями: горизонтальной (a), профильной (b) и фронтально проецирующей (g). На виде сверху отсутствует изображение линий пересечения плоскостей a и b, b и g, определяющих границы выреза, а также линии пересечения этих плоскостей с боковыми гранями пирамиды (граничные линии выреза).

 размеров [2] и заполнению основной надписи чертежа.
размеров [2] и заполнению основной надписи чертежа.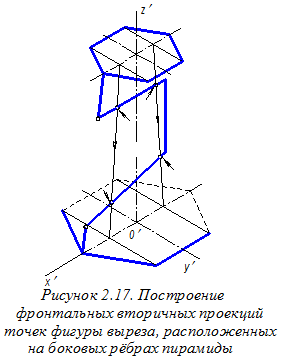

 Для построения аксонометрических проекций 1¢(1 ¢) точек, принадлежащих граничным линиям выреза и расположенных на боковых гранях пирамиды, через фронтальную вторичную проекцию 12¢ º 1 2¢ этих точек проводим прямую, параллельную оси О¢у¢ иоткладываем на ней в обе стороны от указанных точек их ординату m (см. отрезки, помеченные двумя чёрточками). Отрезок 1¢ - 1 ¢; - является нижней границей выреза. Аналогично строим отрезок 2¢ - 2 ¢; - верхнюю границу выреза, используя при этом ординату n этих точек, перенеся её из ортогонального чертежа
Для построения аксонометрических проекций 1¢(1 ¢) точек, принадлежащих граничным линиям выреза и расположенных на боковых гранях пирамиды, через фронтальную вторичную проекцию 12¢ º 1 2¢ этих точек проводим прямую, параллельную оси О¢у¢ иоткладываем на ней в обе стороны от указанных точек их ординату m (см. отрезки, помеченные двумя чёрточками). Отрезок 1¢ - 1 ¢; - является нижней границей выреза. Аналогично строим отрезок 2¢ - 2 ¢; - верхнюю границу выреза, используя при этом ординату n этих точек, перенеся её из ортогонального чертежа


