Построение ортогонального и аксонометрического чертежей правильной шестиугольной призмы

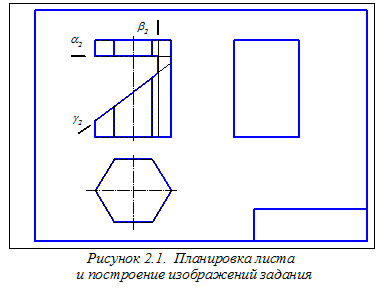
Планировка листа и построение изображений чертежа по размерам, нанесённым на эти изображения в индивидуальном задании, показаны на рисунке 2.1. Изображения включают в себя главный вид, частично вид сверху и габаритный прямоугольник для дальнейшего построения вида слева. Рассматриваемая правильная шестиугольная призма имеет вырез, образованный тремя плоскостями: горизонтальной (a), профильной (b) и фронтально проецирующей (g). На виде сверху отсутствует изображение линий пересечения указанных плоскостей, показывающее границу выреза.

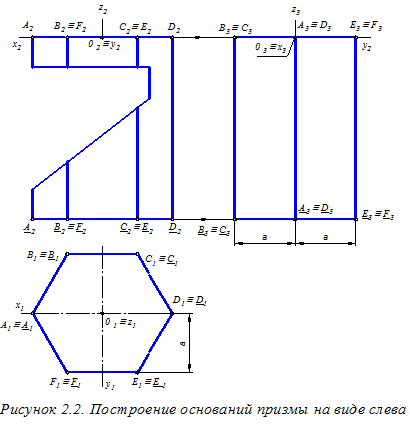Для построения видов сверху и слева, а также аксонометрического изображения данной призмы осуществим привязку этой фигуры к прямоугольной системе координат Оxyz (рисунок 2.2). В качестве горизонтальной координатной плоскости выберем плоскость верхнего основания призмы. На рисунке 2.2 выполнено построение вида слева призмы, не имеющей выреза. При этом используем перенос с вида сверху на вид слева ординаты а некоторых точек нижнего и верхнего оснований призмы. Соединяя соответствующие точки верхнего и нижнего оснований, получаем указанное изображение призмы.

Построим недостающие проекции граничных линий выреза (рисунок 2.3). Граничными линиями выреза (отверстия) будем называть линии пересечения боковых граней призмы с плоскостями a, b и g, формирующими вырез (отверстие). Линии пересечения указанных плоскостей между собой назовём границами выреза (отверстия). На виде сверху по линии проекционной связи строим горизонтальные проекции прямой 1 - 1 пересечения плоскостей a и b, а также прямой 2 – 2 пересечения плоскостей b и g. Проекции указанных прямых на виде сверху совпадают. Изображаем их штриховой линией, т.к. они не видны.

Чтобы не загромождать чертёж, точки, расположенные на боковых рёбрах призмы, не обозначены, так как их построение на видах сверху и слева не вызывает затруднений.

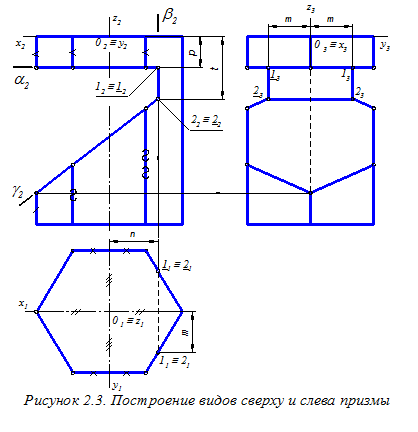Построение обозначенных точек на виде слева выполним переносом с вида сверху на вид слева ординаты m этих точек (см. размер m на рисунке 2.2).

Найденные точки соединяем отрезками прямых, а лишние участки боковых рёбер призмы удаляем. Выполняем обводку построенных изображений. Толщина и форма линий чертежа должна соответствовать ГОСТ 2.303-68 [ 1 ]. В заключение наносим на чертёж необходимые размеры [2] и заполняем основную надпись.

В случае затруднений в построении вида слева рекомендуем предварительно нарисовать или начертить наглядное изображение - аксонометрическую проекцию призмы, используя для этого два построенных вида (главный и сверху).

Краткая теория аксонометрических проекций изложена в пособии «Прямоугольная изометрическая проекция» [3]. Во всех рассматриваемых примерах настоящего пособия будем использовать только прямоугольную изометрическую проекцию.

На отдельном листе ватмана формата А3 или А4 построим аксонометрические оси, расположенные между собой под углом 120° (рисунок 2.4).

На рисунке 2.5 показаны этапы построения аксонометрии верхнего основания призмы – правильного шестиугольника, с учётом ранее выполненной привязки осей. При этом длины обозначенных отрезков измеряем на ортогональном чертеже (см. рисунок 2.3) и откладываем на аксонометрическом.

Для построения боковых рёбер и нижнего основания призмы через точки A¢, B¢, C¢, D¢, E ¢; и F¢; (см. рисунок 2.5) проводим вертикальные отрезки, длина которых равна высоте призмы и, соединяя полученные точки между собой, получим шестиугольник нижнего основания (рисунок 2.6).

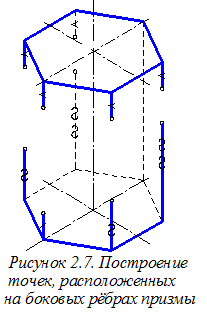
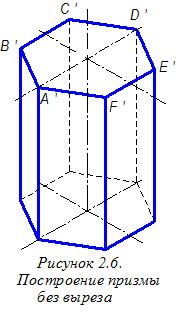
Далее строим точки, принадлежащие граничным линиям выреза и расположенные на боковых рёбрах (рисунок 2.7). Для этого на главном виде (см. рисунок 2.3) измеряем длины соответствующих участков рёбер и откладываем их на аксонометрическом чертеже. Удаляем ненужные отрезки боковых рёбер призмы.

Строим точки граничных линий выреза, расположенные на боковых гранях призмы (рисунок 2.8). Для этого на виде сверху (см. рисунок 2.3) измеряем отрезок «n» и откладываем его на аксонометрическом чертеже по оси О¢х¢; на верхнем основании призмы. Через полученную точку проводим прямую, параллельную оси О¢у¢;, и в пересечении её с линиями верхнего основания призмы находим точки 1₁¢, 1₁ ¢;, 2₁¢, 2 ₁¢;, которые называются вторичными горизонтальными проекциями искомых точек 1, 1, 2, 2.

Из найденных вторичных проекций параллельно оси О¢z, вниз откладываем отрезок длиной р и получаем точки 1¢, 1 ¢; - аксонометрические проекции точек 1 и 1. Соединяя указанные точки между собой, определяем верхнюю границу выреза – линию пересечения плоскостей a и b (см. рисунок 2.3). Откладывая из точек 2₁¢, 2 ₁¢ вниз отрезки длиной t, получаем их аксонометрические проекции. Отрезок 2¢ - 2 ¢ являетсянижней границей выреза. Она образована пересечением плоскостей b и g. Последовательно соединяя найденные аксонометрические проекции точек, лежащих на рёбрах и гранях призмы, завершаем построение аксонометрического чертежа рассматриваемой призмы (рисунок 2.9).

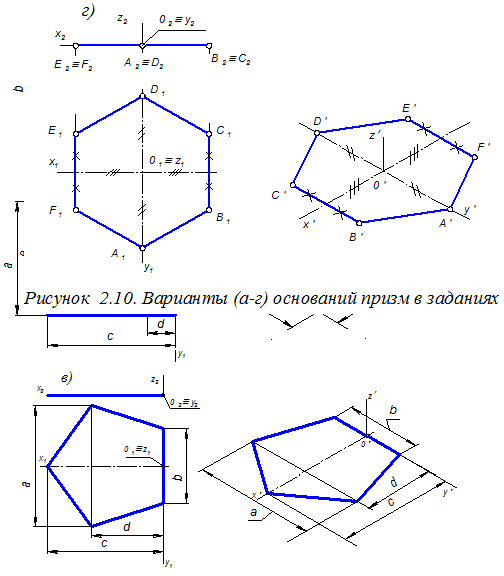
На рисунке 2.10 в качестве примеров показаны варианты построения оснований призм, встречающихся в заданиях по проекционному черчению: а) основание в виде трапеции; б) основание, содержащее элементы прямоугольника и трапеции; в) основание в виде правильного пятиугольника; г) основание в виде правильного шестиугольника, две вершины которого располагаются на координатной оси О¢у¢;.

Аксонометрические проекции указанных плоских фигур построены на основе их ортогональных чертежей. Эти чертежи изображены слева от аксонометрии соответствующей фигуры. Там же даны рекомендуемые варианты привязки основания призмы к прямоугольной системе координат. Возможны иные варианты привязки.

Подчеркнём, что все размеры, нанесённые на изображения ортогонального чертежа основания призмы, переносятся на аксонометрический чертеж параллельно соответствующим аксонометрическим осям. Такой перенос осуществляется измерителем.