Построение аксонометрического чертежа цилиндра вращения
Далее на аксонометрическом чертеже (рисунок 3.8), по «свободной» оси O¢z¢, в обе стороны от начала координат О¢; отложим отрезок t и получим точки B¢; и D¢;, определяющие малую ось эллипса. Для нахождения точек А¢; и С¢;, определяющих большую ось эллипса, из найденных точек B¢; и D¢, как из центров,построим две дуги радиуса R=2t до их взаимного пересечения. Соединяя найденные точки между собой, определим большую ось эллипса.
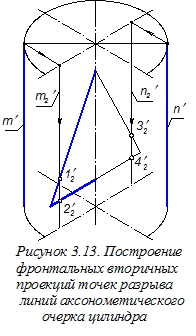
Аксонометрию нижнего основания цилиндра строим смещением вниз на величину h центров О1, О2, О3, О4 дуг овала верхнего основания (рисунок 3.11). Далее строим ¼ часть выреза цилиндра и изображаем фронтальную вторичную проекцию призматического отверстия, образованного плоскостями a, b и g (рисунок 3.12). Размеры a, b и с, необходимые для этого переносим на аксонометрический чертёж из ортогонального чертежа (см. рисунок 3.2) параллельно соответствующим аксонометрическим осям. Обозначим через m¢; и n¢; аксонометрические очерковые образующие цилиндра (рисунок 3.13) и построим их фронтальные вторичные проекции m¢2 и n¢2 (последовательность построений показана стрелками). Далее отметим точки 12¢, 22¢, 32¢, 42¢ - пересечение линий фронтальной вторичной проекции отверстия в цилиндре с фронтальными вторичными проекциями линий аксонометрического очерка и находим точки 1¢, 2¢, 3¢, 4¢ разрыва линий m¢ и n¢ - аксонометрических очерковых образующих конуса граничными линиями отверстия в нём (рисунок 3.14).
Строим овал, определяющий горизонтальную часть призматического отверстия в цилиндре, формируемую плоскостью a (рисунок 3.17). Для этого можно использовать дуги R и r овала верхнего основания конуса, найдя новые центры этих дуг. У построенного овала сохраняем лишь те его участки, которые видны в аксонометрии.
Подчеркнём, что окончательное оформление аксонометрического чертежа рассматриваемого цилиндра требует плавного соединения всех полученных точек при изображении сквозного отверстия и обводку всех видимых линий контура изображения цилиндра. 3.4. Построение ортогонального и аксонометрического чертежей Переходим к рассмотрению в задаче 2 построения ортогонального и аксонометрического чертежей конуса вращения. На рисунке 3.20 показаны изображения: главный вид и частично вид сверху прямого кругового усечённого конуса, а также габаритный прямоугольник для последующего построения вида слева. Рассматриваемый конус имеет сквозное отверстие, образованное тремя плоскостями: горизонтальной плоскостью a, рассекающей коническую поверхность по окружности, и двумя фронтально проецирующими плоскостями b и g, рассекающими его поверхность по эллипсам. Для построения видов сверху и слева, а также аксонометрического изображения данного конуса осуществим привязку этой фигуры к прямоугольной системе координат Оxyz (рисунок 3.21). В качестве горизонтальной координатной плоскости выберем плоскость нижнего основания конуса.
Аналогично определяем горизонтальные проекции точек 4, 5 и 6 граничных линий отверстия, расположенных в плоскости b (рисунок 3.22). Для этого строим окружности радиуса R 1, R 2 и R 3, расположенные в промежуточных горизонтальных плоскостях a 1, a 2, a 3. Аналогично строим на виде сверху точки граничных линий отверстия, расположенных в плоскости g. Последовательно соединяем найденные горизонтальные проекции точек плавными кривыми. Окончательное оформление вида сверху показано на рисунке 3.23. Здесь линиями невидимого контура показаны линии пересечения плоскостей a и b, g и b, a и g. Построение профильных проекций рассматриваемых точек (см. рисунок 3.23) осуществляем как по линиям связи (точки 33 и 63) на линиях профильного очерка конуса, так и переносом отрезков ординат точек с вида сверху на вид слева. Переносимые отрезки показаны одинаковыми символами как на виде сверху, где они измеряются, так и на виде слева, где они откладываются. Последовательно соединяем найденные профильные проекции точек
плавной кривой, а также изображаем линии невидимого контура, определяющие линии пересечения плоскостей a и b, g и b, a и g.
Более подробная информация о правилах построения и обозначения разрезов в соответствии с ГОСТ 2.305 – 68 приведена в разделе 3.2.
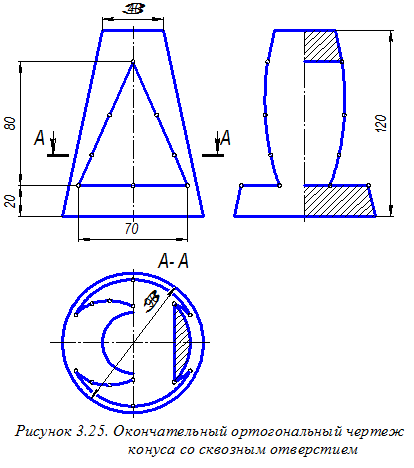
Построим прямоугольную изометрическую проекцию рассматриваемого конуса, используя привязку к нему ортогональной системы координат Оxyz, выполненную ранее (см. рисунок 3.21). На отдельном листе ватмана формата А3 или А4 изобразим аксонометрические оси (см. рисунок 2.4). Далее построим аксонометрические проекции окружностей нижнего и верхнего оснований конуса. Такими проекциями будут два эллипса, центры которых располагаются на координатной оси O¢z¢; и смещены относительно друг друга на расстояние h (рисунок 3.26). Эллипсы имеют следующее соотношение большой и малой осей: Б.о. = 1,22 d, М.о. = 0,71 d, - где d - диаметр изображаемой окружности. Малая ось эллипсов располагается вдоль «свободной» координатной оси O¢z¢;, а её размер равен длине стороны квадрата, вписанного в изображаемую окружность. Для удобства построений вместо эллипсов изображаем овалы (см. рисунки 3.9 и 3.10). При этом используем графическое определение как малых полуосей эллипсов (см. на рисунке 3.20, на виде сверху отрезки t и t¢), так и больших полуосей (см. рисунок 3.8). Далее строим прямые m¢; и n¢, являющиеся аксонометрическим очерком конической поверхности (рисунок 3.27). При этом определяем точки касания этими линиями эллипсов, являющихся основаниями конуса. Для этого удлиняем образующие а¢; и b¢ до точек А¢; и В¢; пересечения этих линий с верхним основанием конуса. Образующие а¢; и b¢ вместе с осевой линией чертежа образуют три прямые, проходящие через вершину конyса. Эта вершина на чертеже недоступна. Указанные три прямые пересекают эллипсы (овалы) оснований в шести точках. Соединяем точки пересечения с
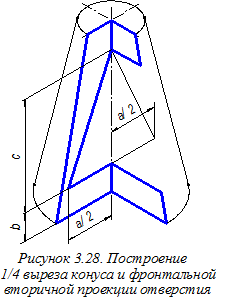
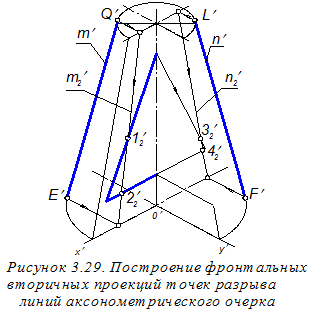
существу строим фронтальные вторичные проекции плоскостей a, b и g, формирующих отверстие в конусе (рисунок 3.28). При этом размеры a, b и c из ортогонального чертежа (см. главный вид на рисунке 3.23) переносим на аксонометрический чертёж параллельно соответствующим аксонометрическим осям. Далее необходимо построить точки 1¢, 2¢, 3¢ и 4¢; разрыва линий аксонометрического очерка конуса граничными линиями отверстия в нём. Однако перед этим предварительно определим их фронтальные вторичные проекции 12¢, 22¢, 32¢, 42¢ (рисунок 3.29). Для этого сначала строим фронтальные вторичные проекции m2¢, n2¢ очерковых образующих конуса и находим точки пересечения этих проекций с линиями вторичной проекции отверстия. Последовательность этих построений показана стрелками. При этом подчеркнём, что построения начинаются не в конечных точках больших осей эллипсов (овалов), а в граничных точках E¢;, F¢, Q¢;, L¢; аксонометрических очерковых образующих, построенных ранее. Далее находим искомые точки 1¢, 2¢, 3¢ и 4¢; (рисунок 3.30). Строим аксонометрические проекции промежуточных точек граничных линий отверстия. Для этого сначала на линиях фронтальной вторичной проекции отверстия намечаем промежуточные точки (рисунок 3.31). При этом используем размеры g и f, перенося их из ортогонального чертежа (см. рисунок 3.23). Далее через найденные вторичные проекции проводим прямые, параллельные оси О¢у¢;, и откладыванием на них в обе стороны ординаты искомых
Выполняем штриховку участков конуса, расположенных в координатных плоскостях хОz и уОz. Определение направлений линий штриховки в прямоугольной изометрии показано на рисунке 3.19. Окончательное оформление аксонометрического чертежа конуса со сквозным отверстием (рисунок 3.34) требует тщательной обводки всех линий изображения: дуги овалов обводятся циркулем, а другие кривые – с помощью лекала. 4. Построение ортогонального и аксонометрического чертежей детали Планировка листа и построение изображений детали по размерам, нанесённым на эти изображения в индивидуальном задании, показаны на рисунке 4.1. Изображения включают в себя: главный вид, вид сверху, а также габаритный прямоугольник для дальнейшего построения вида слева. Для построения вида слева и аксонометрического чертежа детали осуществим привязку детали к прямоугольной системе координат О xyz (рисунок 4.2). За горизонтальную координатную плоскость примем плоскость верхнего основания цилиндрической плиты, срезанной по бокам двумя фронтальными плоскостями, и имеющей два полуовальных выреза. На этой плите расположен цилиндр вращения, ось которого совпадает с координатной осью Оz. Его подкрепляют два ребра жёсткости – призматические элементы треугольной формы. Внутренняя форма детали состоит из сквозного ступенчатого цилиндрического отверстия.
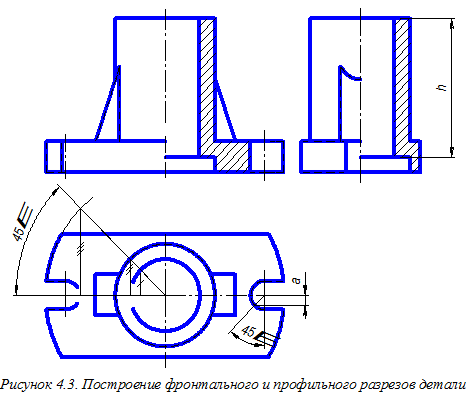
Обращаем внимание на условность, принятую в машиностроительном черчении, - при продольном разрезе ребра жёсткости его контур не заштриховывается. Более подробная информация о разрезах приведена в подразделе 3.2.
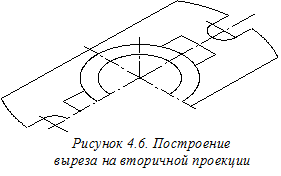
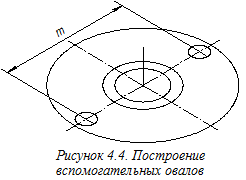
Напомним, что круглое основание любого цилиндрического или конического элемента детали, расположенное в координатной плоскости или параллельно такой плоскости, в прямоугольной изометрии изображается эллипсом, имеющим следующее соотношение большой и малой осей: Б.о. = 1,22 d, М.о. = 0,71 d, - где d - диаметр изображаемой окружности. Малая ось эллипсов располагается вдоль «свободной» координатной оси, - оси, перпендикулярной плоскости, в которой расположена изображаемая окружность,а размер малой оси равен длине стороны квадрата, вписанного в изображаемую окружность. Для удобства построения и получения лучшего качества изображения на аксонометрическом чертеже вместо эллипсов строим овалы – циркульные кривые (см. рисунки 3.9 и 3.10). Поэтому сначала строим овалы, определяющие горизонтальные вторичные проекции всех цилиндрических элементов детали (рисунок 4.4). Для графического определения малых полуосей эллипсов используем построения, показанные на рисунке 4.3 (см. размер а и отрезки, помеченные штрихами). Размеры b, c, m и n, используемые для построений, переносим с ортогонального чертежа (см. рисунок 4.2).Далее строим прямые, определяющие горизонтальные вторичные проекции плоских элементов детали (рисунок 4.5). На следующем этапе построения аксонометрии удаляем ненужные линии чертежа с учётом выполнения в дальнейшей выреза ¼ детали (рисунок 4.6).
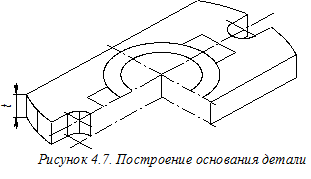
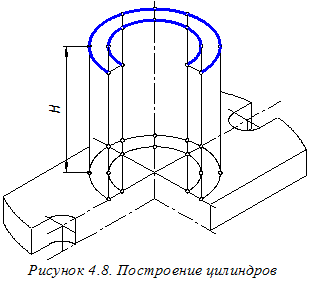
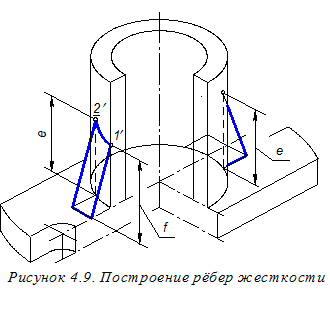
Далее создадим объёмное изображение основания детали (рисунок 4.7). Для этого из точек горизонтальной вторичной проекции основания детали, расположенных ближе к наблюдателю, строим вспомогательные прямые, параллельные оси О¢ z¢, и на них откладываем вниз отрезки длиной t, определяющей толщину плиты основания. Таким образом, определяем точки контура нижней части основания. Изображения плоских участков основания выполняем лишь по их граничным точкам, а для цилиндрических участков строим и промежуточные точки. Длину отрезка t определяем на ортогональном чертеже (см. рисунок 4.2). Соединяя найденные точки нижней плоскости основания прямыми или плавными кривыми и удаляя ненужные вспомогательные вертикальные отрезки, построим основание детали. Аналогично с помощью вспомогательных вертикальных отрезков длиной Н, используя горизонтальные вторичные проекции цилиндрических элементов, можно построить точки верхнего основания этих элементов детали (рисунок 4.8). Найденные точки соединяем плавными кривыми, а вспомогательные вертикальные отрезки и невидимые линии чертежа удаляем. Для построения изображения рёбер жёсткости находим точки 1¢; и 2 ¢; (рисунок 4.9). Для этого из соответствующих точек горизонтальных вторичных проекций рёбер строим вспомогательные вертикальные отрезки длиной е и f. Длины этих отрезков измеряем на ортогональном чертеже (см. рисунок 4.2). Строим лишь видимые элементы рёбер, а невидимые удаляем.
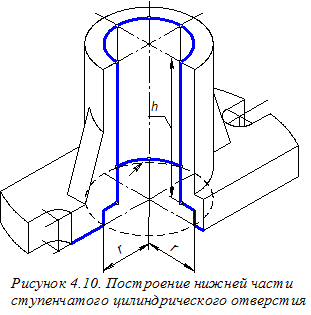
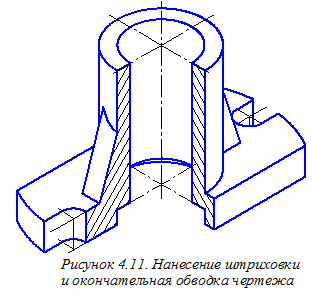
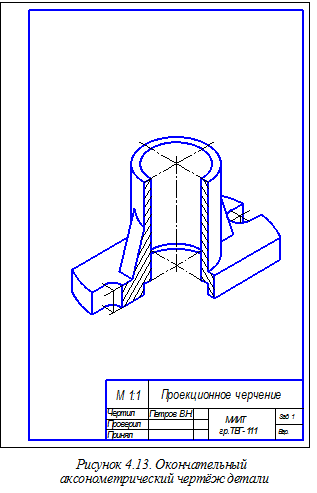
Для изображения в аксонометрии видимой части окружности радиуса r цилиндрического углубления, расположенного в нижней части детали, строим образующие этой цилиндрической поверхности, попадающие в вырез ¼ части детали и овал, соответствующий окружности цилиндрического углубления, расположенной в нижней плоскости основания детали (см. на рисунке 4.10 овал, изображённый штриховой линией). У построенного овала сохраняем В заключение производим обводку чертежа и наносим штриховку (рисунок 4.11). Определение направлений линий штриховки в аксонометрии показано на рисунке 3.19. Окончательное оформление аксонометрического чертежа детали требует плавного (с помощью лекал) соединения построенных точек кривых линий, изображающих как элементы сквозного ступенчатого цилиндрического отверстия в детали, так и элементы её внешней формы. Завершается оформление чертежа заполнением его основной надписи. Окончательно оформленные ортогональный и аксонометрический чертежи детали показаны соответственно на рисунках 4.12 и 4.13. Отметим также, что во всех рассмотренных ранее построениях измерение размеров на ортогональном чертеже и перенос их на аксонометрический чертеж производилось с помощью измерителя. На изображениях ортогонального и аксонометрического чертежей рекомендуется сохранять характерные и вспомогательные точки построенных линий, без обозначения этих точек. Литература 1. Единая система конструкторской документации. Общие правила выполнения чертежей. М., 1991,453 с. 2. Аверин В.Н., Куколева И Ф. Нанесение размеров на чертежах. Методические указания к практическим занятиям по инженерной графике. М.: МИИТ, 2008. 37 с. 3. Аверин В.Н., Пуйческу Ф.И. Прямоугольная изометрическая проекция. Методические указания к практическим занятиям по инженерной графике. М.: МИИТ, 2008. 23 с.
Учебно-методическое издание
|

 Построение прямоугольной изометрической проекции рассматриваемого цилиндра с учётом ранее выполненной привязки этой фигуры к прямоугольной системе координат Оxyz (см. рисунок 3.2) начнём с изображения аксонометрических осей (см. рисунок 2.4) на отдельном листе ватмана формате А3 или А4.
Построение прямоугольной изометрической проекции рассматриваемого цилиндра с учётом ранее выполненной привязки этой фигуры к прямоугольной системе координат Оxyz (см. рисунок 3.2) начнём с изображения аксонометрических осей (см. рисунок 2.4) на отдельном листе ватмана формате А3 или А4.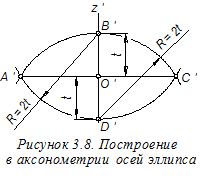 Далее построим аксонометрическую проекцию окружности верхнего основания цилиндра. Такой проекцией является эллипс, имеющий следующее соотношение большой и малой осей: Б.о. = 1,22 d, М.о. = 0,71 d, - где d - диаметр изображаемой окружности. Малая ось эллипса всегда располагается вдоль «свободной» координатной оси. «Свободной» называют координатную ось, перпендикулярную плоскости, в которой расположена изображаемая окружность. В рассматриваемом примере окружности оснований цилиндра располагаются в плоскостях, параллельных П1 и «свободной» является ось Oz.
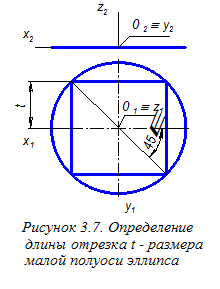
Далее построим аксонометрическую проекцию окружности верхнего основания цилиндра. Такой проекцией является эллипс, имеющий следующее соотношение большой и малой осей: Б.о. = 1,22 d, М.о. = 0,71 d, - где d - диаметр изображаемой окружности. Малая ось эллипса всегда располагается вдоль «свободной» координатной оси. «Свободной» называют координатную ось, перпендикулярную плоскости, в которой расположена изображаемая окружность. В рассматриваемом примере окружности оснований цилиндра располагаются в плоскостях, параллельных П1 и «свободной» является ось Oz.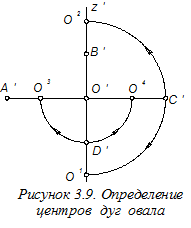 Сначала графически определим размеры осей эллипса. Известно, что в прямоугольной изометрической проекции размер малой оси эллипса равен длине стороны квадрата, вписанного в изображаемую окружность. Поэтому на виде сверху чертежа цилиндра построим такой квадрат (рисунок 3.7) и определим длину отрезка t – половины стороны квадрата. В последующем для упрощения построений при определении на ортогональном чертеже длины отрезка t будет использована лишь линия, расположенная под углом 45° к координатным осям (без изображения квадрата целиком).
Сначала графически определим размеры осей эллипса. Известно, что в прямоугольной изометрической проекции размер малой оси эллипса равен длине стороны квадрата, вписанного в изображаемую окружность. Поэтому на виде сверху чертежа цилиндра построим такой квадрат (рисунок 3.7) и определим длину отрезка t – половины стороны квадрата. В последующем для упрощения построений при определении на ортогональном чертеже длины отрезка t будет использована лишь линия, расположенная под углом 45° к координатным осям (без изображения квадрата целиком).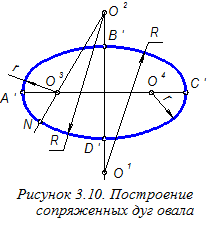 Построим вместо эллипса овал - замкнутую кривую, представляющую собой четыре последовательно сопряжённые дуги окружностей радиуса R и r. Для этого сначала определим центры этих дуг (рисунок 3.9). Центры О1 и О2 дуг радиуса R определим на оси O¢z¢ в точках пересечения её с окружностью радиуса, равного большой полуоси эллипса, а центры О3 и О4 дуг радиуса r определяем в точках пересечения большой оси эллипса с окружностью радиуса, равного малой полуоси эллипса. После этого определяются и радиусы дуг:
Построим вместо эллипса овал - замкнутую кривую, представляющую собой четыре последовательно сопряжённые дуги окружностей радиуса R и r. Для этого сначала определим центры этих дуг (рисунок 3.9). Центры О1 и О2 дуг радиуса R определим на оси O¢z¢ в точках пересечения её с окружностью радиуса, равного большой полуоси эллипса, а центры О3 и О4 дуг радиуса r определяем в точках пересечения большой оси эллипса с окружностью радиуса, равного малой полуоси эллипса. После этого определяются и радиусы дуг: 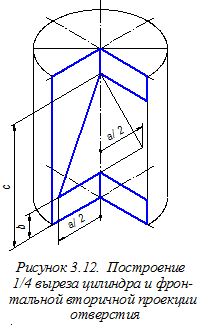
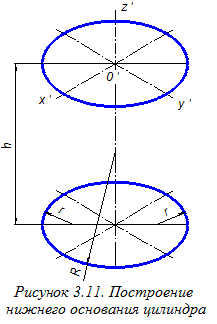
 О2 и О3 рассматриваемых дуг.
О2 и О3 рассматриваемых дуг.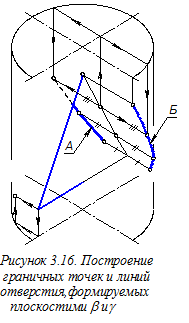
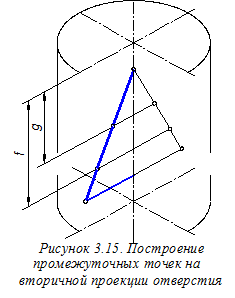 Строим в аксонометрии граничные линии отверстия. Для этого сначала на вторичной фронтальной проекции отверстия находим промежуточные точки (рисунок 3.15), используя размеры g и f, перенесённые из ортогонального чертежа (см. главный вид на рисунке 3.2).С помощью указанных вторичных проекций строим аксонометрические проекции промежуточных точек, расположенных на граничных линиях отверстия в цилиндре. Последовательность построения этих точек показана на рисунке 3.16 стрелками. Отрезки, длины которых использованы при по
Строим в аксонометрии граничные линии отверстия. Для этого сначала на вторичной фронтальной проекции отверстия находим промежуточные точки (рисунок 3.15), используя размеры g и f, перенесённые из ортогонального чертежа (см. главный вид на рисунке 3.2).С помощью указанных вторичных проекций строим аксонометрические проекции промежуточных точек, расположенных на граничных линиях отверстия в цилиндре. Последовательность построения этих точек показана на рисунке 3.16 стрелками. Отрезки, длины которых использованы при по 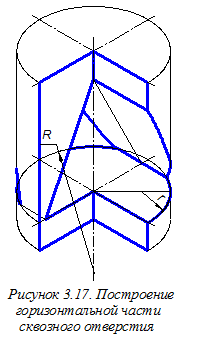 строении аксонометрических
строении аксонометрических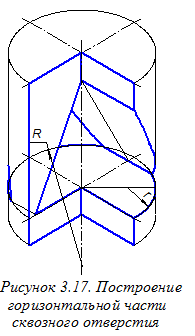 проекций промежуточных точек, помечены штрихами на рисунках 3.2 и 3.16. Соединяя полученные точки, плавной кривой, получим изображения тех граничных линий отверстия в цилиндре, которые формируются плоскостью g. Эти линии помечены на рисунке 3. 16 стрелками А и Б. Аналогично можно построить точки и изображение граничной линии отверстия, формируемой плоскостью b. Однако основная часть этих точек не видна и поэтому не требуется их построение.
проекций промежуточных точек, помечены штрихами на рисунках 3.2 и 3.16. Соединяя полученные точки, плавной кривой, получим изображения тех граничных линий отверстия в цилиндре, которые формируются плоскостью g. Эти линии помечены на рисунке 3. 16 стрелками А и Б. Аналогично можно построить точки и изображение граничной линии отверстия, формируемой плоскостью b. Однако основная часть этих точек не видна и поэтому не требуется их построение.
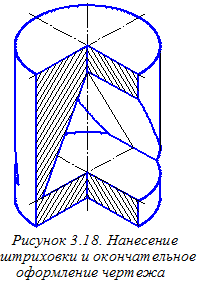 Для окончательного оформления аксонометрического чертежа цилиндра наносим штриховку тех элементов выреза цилиндра, которые располагаются в плоскостях хОz и уОz (рисунок 3.18). Определить направление линий штриховки в аксонометрии по указанным координатным плоскостям можно следующим образом (рис. 3.19). Построим окружность произвольного радиуса с центром в начале координат и соединим между собой точки пересечения этой окружности с координатными осями, определяющими рассматриваемые плоскости. Построенные отрезки и определят направления линий штриховки по указанным плоскостям.
Для окончательного оформления аксонометрического чертежа цилиндра наносим штриховку тех элементов выреза цилиндра, которые располагаются в плоскостях хОz и уОz (рисунок 3.18). Определить направление линий штриховки в аксонометрии по указанным координатным плоскостям можно следующим образом (рис. 3.19). Построим окружность произвольного радиуса с центром в начале координат и соединим между собой точки пересечения этой окружности с координатными осями, определяющими рассматриваемые плоскости. Построенные отрезки и определят направления линий штриховки по указанным плоскостям.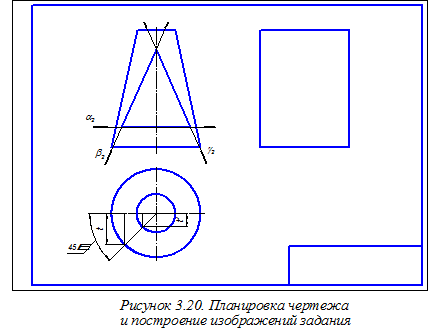 На главном виде отмечаем характерные и промежуточные точки граничных линий отверстия и выполняем их построение на виде сверху.
На главном виде отмечаем характерные и промежуточные точки граничных линий отверстия и выполняем их построение на виде сверху.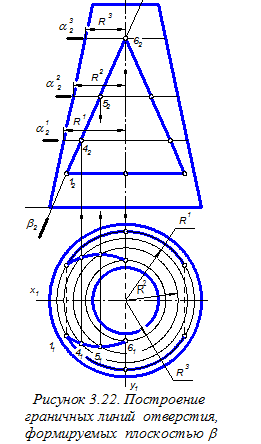
 Сначала рассмотрим точки 1, 2, 3, расположенные на горизонтальных граничных линиях отверстия, формируемых плоскостью a (см. рисунок 3.21). Эти точки (всего их шесть) определяем на виде сверху по линиям связи на окружности радиуса R. Указанный радиус измеряем на главном виде, в плоскости a от оси конуса до его очерковой образующей.
Сначала рассмотрим точки 1, 2, 3, расположенные на горизонтальных граничных линиях отверстия, формируемых плоскостью a (см. рисунок 3.21). Эти точки (всего их шесть) определяем на виде сверху по линиям связи на окружности радиуса R. Указанный радиус измеряем на главном виде, в плоскости a от оси конуса до его очерковой образующей.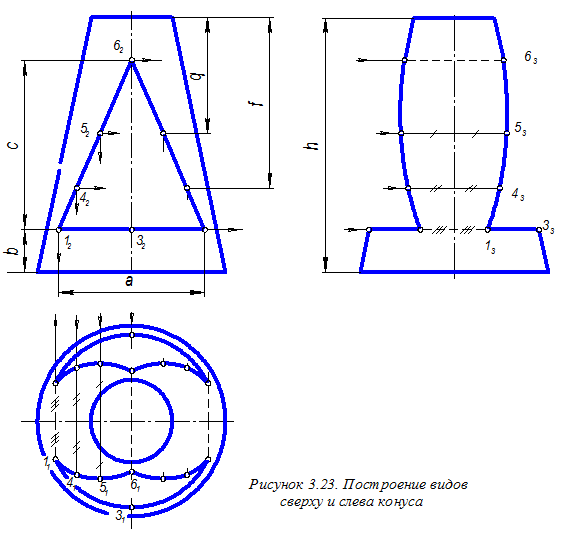
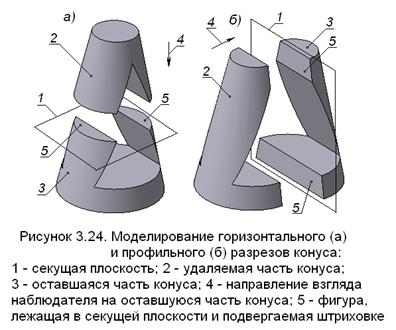 Далее строим горизонтальный и профильный разрезы конуса. Моделирование горизонтального и профильного разрезов конуса, имеющего сквозное отверстие, показано на рисунке 3.24. Изображение горизонтального разреза выполняем на виде сверху, а профильного – на виде слева (рисунок 3.25). В обоих случаях совмещаем половину соответствующего вида с половиной разреза, используя вертикальную осевую линию в качестве границы между этими изображениями. На совместном изображении разрезы располагаем справа от границы, а виды слева от неё. Производим обозначение горизонтального разреза. После построения на чертеже необходимых разрезов на всех его изображениях удаляем линии невидимого контура.
Далее строим горизонтальный и профильный разрезы конуса. Моделирование горизонтального и профильного разрезов конуса, имеющего сквозное отверстие, показано на рисунке 3.24. Изображение горизонтального разреза выполняем на виде сверху, а профильного – на виде слева (рисунок 3.25). В обоих случаях совмещаем половину соответствующего вида с половиной разреза, используя вертикальную осевую линию в качестве границы между этими изображениями. На совместном изображении разрезы располагаем справа от границы, а виды слева от неё. Производим обозначение горизонтального разреза. После построения на чертеже необходимых разрезов на всех его изображениях удаляем линии невидимого контура.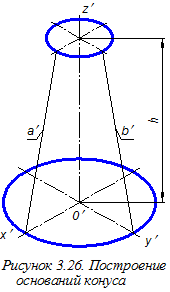
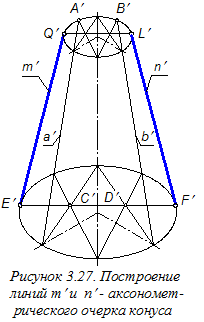
 овалом смежных прямых крест на крест, а через точки их пересечений (см., например точки С¢; и D¢;) проводим прямые до пересечения с эллипсами (см. точки E¢;, F¢, Q¢;, L¢;). Найденные точки нижнего и верхнего оснований конуса соединяем отрезками прямых. Это и будут линии аксонометрического очерка конуса.
овалом смежных прямых крест на крест, а через точки их пересечений (см., например точки С¢; и D¢;) проводим прямые до пересечения с эллипсами (см. точки E¢;, F¢, Q¢;, L¢;). Найденные точки нижнего и верхнего оснований конуса соединяем отрезками прямых. Это и будут линии аксонометрического очерка конуса.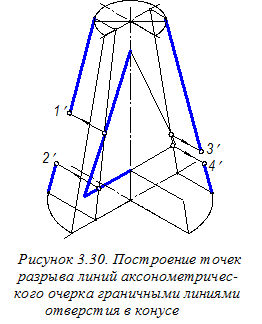
 Затем выполняем вырез ¼ части конуса и строим фронтальную вторичную проекцию призматического отверстия в конусе, т. е. по
Затем выполняем вырез ¼ части конуса и строим фронтальную вторичную проекцию призматического отверстия в конусе, т. е. по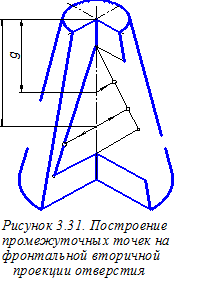 точек (рисунок 3.32). Ординаты промежуточных точек, помеченные штрихами, переносим из
точек (рисунок 3.32). Ординаты промежуточных точек, помеченные штрихами, переносим из 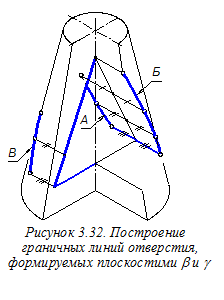 ортогонального чертежа (см. рисунок 3.23) на аксонометрический чертёж. При этом изображаем лишь точки, видимые на аксонометрическом чертеже. Последовательно соединяя найденные точки плавными кривыми (дугами эллипсов), строим видимые участки граничных линий отверстия в конусе, формируемые плоскостью b (см. на рисунке 3.32 линии А и Б) и плоскостью g (см. линию В).
ортогонального чертежа (см. рисунок 3.23) на аксонометрический чертёж. При этом изображаем лишь точки, видимые на аксонометрическом чертеже. Последовательно соединяя найденные точки плавными кривыми (дугами эллипсов), строим видимые участки граничных линий отверстия в конусе, формируемые плоскостью b (см. на рисунке 3.32 линии А и Б) и плоскостью g (см. линию В).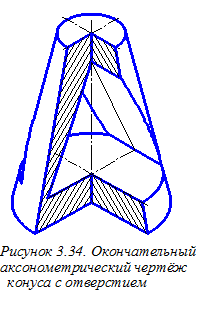
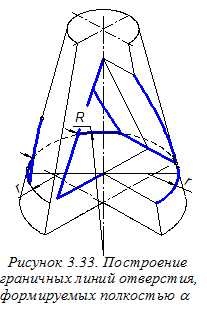 Строим овал, определяющий граничные линии горизонтальной части отверстия в конусе и формируемые плоскостью a (рисунок 3.33). Границы видимости условно показаны стрелками. Изображаем прямую, являющуюся линией пересечением плоскостей a и g.
Строим овал, определяющий граничные линии горизонтальной части отверстия в конусе и формируемые плоскостью a (рисунок 3.33). Границы видимости условно показаны стрелками. Изображаем прямую, являющуюся линией пересечением плоскостей a и g.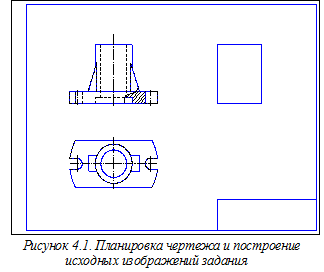 При построении вида слева особый интерес представляет построение дуги эллипса, образованного пересечением цилиндра с наклонной гранью ребра жёсткости. Построение выполнено по трём точкам (1, 2 и 2) путём переноса с вида сверху на вид слева ординаты точек 2 и 2, равной полуширине ребра жёсткости (см. размер b/2). Точка 1 в принятой системе координат имеет нулевую ординату.
При построении вида слева особый интерес представляет построение дуги эллипса, образованного пересечением цилиндра с наклонной гранью ребра жёсткости. Построение выполнено по трём точкам (1, 2 и 2) путём переноса с вида сверху на вид слева ординаты точек 2 и 2, равной полуширине ребра жёсткости (см. размер b/2). Точка 1 в принятой системе координат имеет нулевую ординату.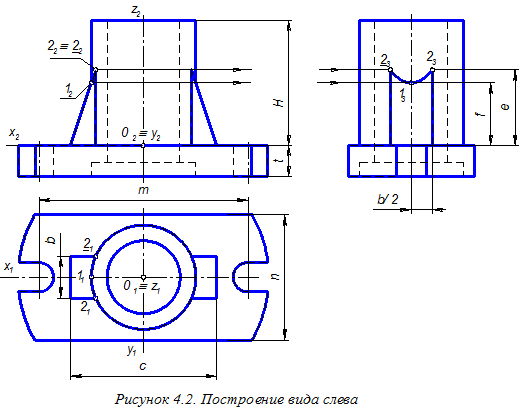
 Построение прямоугольной изометрической проекции рассматриваемой детали с учётом привязки её к прямоугольной системе координат, выполненной ранее (см. рисунок 4.2), начнём с изображения аксонометрических осей (см. рисунок 2.4) на отдельном листе ватмана формата А3 или А4.
Построение прямоугольной изометрической проекции рассматриваемой детали с учётом привязки её к прямоугольной системе координат, выполненной ранее (см. рисунок 4.2), начнём с изображения аксонометрических осей (см. рисунок 2.4) на отдельном листе ватмана формата А3 или А4.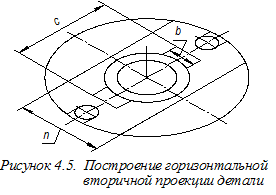
 Удалив все невидимые линии чертежа, включая вторичные проекции цилиндров и рёбер жёсткости, построенные ранее, приступаем к изображению элементов нижней части ступенчатого цилиндрического отверстия (рисунок 4.10). Построение нижней видимой части окружности цилиндрического отверстия меньшего радиуса осуществляем с помощью вспомогательных вертикальных отрезков длиной h, проведенных вниз из пяти точек верхнего основания этого отверстия. Три из пяти построенных точек соединяем плавной кривой.
Удалив все невидимые линии чертежа, включая вторичные проекции цилиндров и рёбер жёсткости, построенные ранее, приступаем к изображению элементов нижней части ступенчатого цилиндрического отверстия (рисунок 4.10). Построение нижней видимой части окружности цилиндрического отверстия меньшего радиуса осуществляем с помощью вспомогательных вертикальных отрезков длиной h, проведенных вниз из пяти точек верхнего основания этого отверстия. Три из пяти построенных точек соединяем плавной кривой.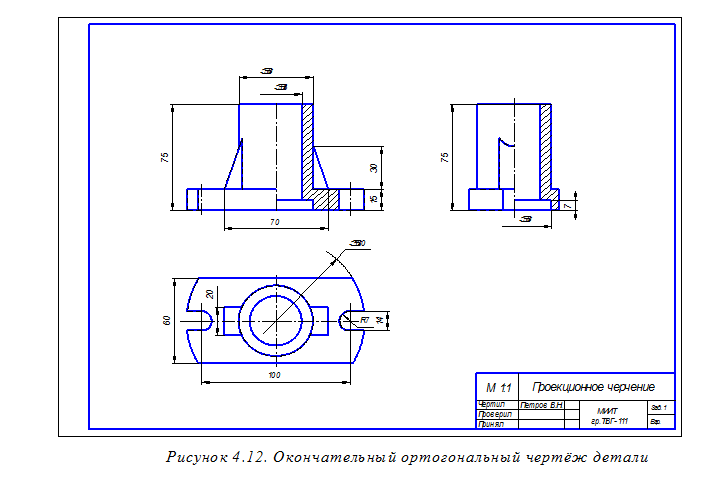
 лишь его видимую часть, показанную на рисунке 4.10 стрелкой.
лишь его видимую часть, показанную на рисунке 4.10 стрелкой.


