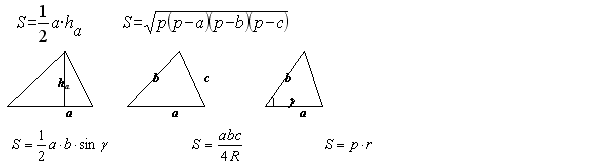Формулы
Обозначения:
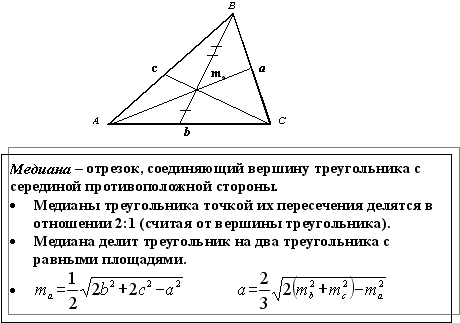
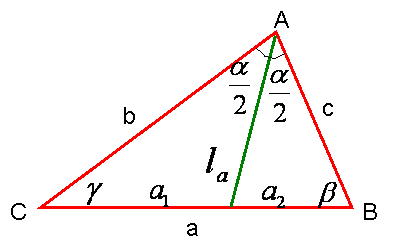
l a — биссектриса, проведенная к стороне a, _______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________ Медиана Медианой треугольника, проведенной из данной вершины, называется отрезок, соединяющий эту вершину с серединой противолежащей стороны треугольника.
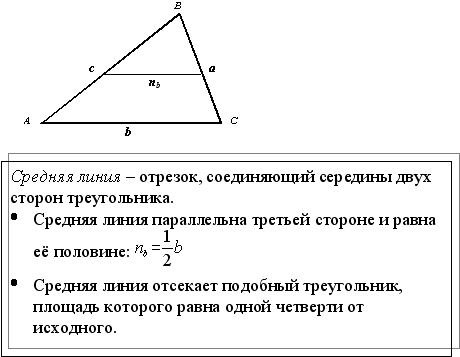
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________ Средняя линия Отрезок, соединяющий середины противолежащих сторон четырехугольника, называется средней линией четырехугольника. Если в выпуклом четырехугольнике прямая, проходящая через середины двух противоположных сторон, образует равные углы с диагоналями четырехугольника, то диагонали равны. Средняя линия треугольника - это отрезок, соединяющий середины двух его сторон. Средняя линия треугольника параллельна третьей стороне, а ее длина равна половине длины этой стороны. Отрезок, соединяющий середины боковых сторон трапеции, называется средней линией трапеции. Теорема. Средняя линия трапеции параллельна основаниям, а длина ее равна полусумме длин оснований. Теорема. Середины сторон равнобедренной трапеции являются вершинами ромба.
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________ Площадь треугольника Обозначения:
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
|

 cb (b + c + a)(b + c − a)
la = c + b 2 b
cb (b + c + a)(b + c − a)
la = c + b 2 b  c
c  la = hacos 2
la = hacos 2  −
−  la =
la = 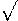 b
b  c − a 1
c − a 1 

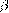
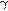 — внутренние углы треугольника при вершинах a, b, c соответственно,
— внутренние углы треугольника при вершинах a, b, c соответственно,