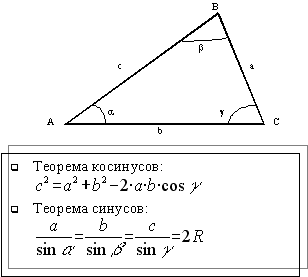
Для решения произвольных треугольников существует теорема косинусов и теорема синусов.
Теорема косинусов. Квадрат стороны треугольника равен сумме квадратов двух других сторон без удвоенного произведения этих сторон на косинус угла между ними.
Формула a 2= b 2+ c 2−2 b  c
c  cos
cos 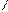 A (или формула b 2= a 2+ c 2−2 a
A (или формула b 2= a 2+ c 2−2 a  c
c  cos
cos 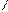 B или формула c 2= b 2+ a 2−2 b
B или формула c 2= b 2+ a 2−2 b  a
a  cos
cos 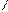 C) позволяет вычислить длину одной из сторон треугольника по данным длинам двух других сторон и величине угла, лежащей против неизвестной стороны.
C) позволяет вычислить длину одной из сторон треугольника по данным длинам двух других сторон и величине угла, лежащей против неизвестной стороны.
Теорема косинусов позволяет также по даннм величинам сторон треугольника вычислить величины его углов:
cos 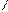 A =2 b
A =2 b  cb 2+ c 2− a 2; cos
cb 2+ c 2− a 2; cos 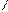 B =2 a
B =2 a  ca 2+ c 2− b 2; cos
ca 2+ c 2− b 2; cos 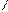 C =2 a
C =2 a  ba 2+ b 2− c 2.
ba 2+ b 2− c 2.
Теорема синусов. Стороны треугольника пропорционально синусам противоположных углов asin 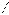 A = bsin
A = bsin 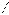 B = csin
B = csin 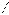 C, где a, b, c - стороны треугольника.
C, где a, b, c - стороны треугольника.
Теорема синусов позволяет по двум сторонам и углу, лежащему против одной из них (или по стороне и двум углам) вычислить остальные элементы треугольника.
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Прямоугольный треугольник
Треугольник называют прямоугольным, если у него есть прямой угол.
Прямоугольный треугольник имеет две взаимно перпендикулярные стороны, называемые катетами; третья его сторона называется гипотенузой.
- По свойствам перпендикуляра и наклонных гипотенуза длиннее каждого из катетов (но меньше их суммы).
- Сумма двух острых углов прямоугольного треугольника равна прямому углу.
- Две высоты прямоугольного треугольника совпадают с его катетами. Поэтому одна из четырех замечательных точек попадает в вершины прямого угла треугольника.
- Центр описанной окружности прямоугольного треугольника лежит в середине гипотенузы.
- Медиана прямоугольного треугольника, проведенная из вершины прямоуго угла на гипотенузу, является радиусом описанной около этого треугольника окружности.
Рассмотрим произвольный прямоугольный треугольник АВС и проведем высоту СD = hc из вершины С его прямого угла.
Она разобьет данный треугольник на два прямоугольных треугольника АСD и ВСD; каждый из этих треугольников имеет с треугольником АВС общий острый угол и потому подобен треугольнику АВС.
Все три треугольника АВС, АСD и ВСD подобны между собой.
Из подобия треугольников определяются соотношения:
- h =
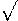 ac
ac  bc = ca
bc = ca  b;
b; - c = ac + bc;
- a =
 ac
ac  c
c  b =
b = 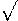 bc
bc  c;
c; - (ab)2= acbc.
Теорема Пифагора — одна из основополагающих теорем евклидовой геометрии, устанавливающая соотношение между сторонами прямоугольного треугольника.
Геометрическая формулировка. В прямоугольном треугольнике площадь квадрата, построенного на гипотенузе, равна сумме площадей квадратов, построенных на катетах.
Алгебраическая формулировка. В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
То есть, обозначив длину гипотенузы треугольника через c, а длины катетов через a и b:
a 2 + b 2 = c 2
Обратная теорема Пифагора. Для всякой тройки положительных чисел a, b и c, такой, что
a 2 + b 2 = c 2,
существует прямоугольный треугольник с катетами a и b и гипотенузой c.
Признаки равенства прямоугольных треугольников:
- по катету и гипотенузе;
- по двум катетам;
- по катету и острому углу;
- по гипотенузе и острому углу.

_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Равнобедренный треугольник
Равнобедренный треугольник — треугольник, в котором две стороны равны между собой.
По определению, правильный треугольник также является равнобедренным, но обратное, вообще говоря, неверно.

| Свойства
- Углы, противолежащие равным сторонам равнобедренного треугольника, равны между собой.
- Также равны биссектрисы, медианы и высоты, проведённые из этих углов.
- Биссектриса, медиана и высота, проведенные к основанию совпадают между собой.
- Центры вписанной и описанной окружностей лежат на этой линии.
- Углы, противолежащие равным сторонам, всегда острые (следует из их равенства).
Признаки
- Два угла треугольника равны.
- Высота совпадает с медианой.
- Высота совпадает с биссектрисой.
- Биссектриса совпадает с медианой.
|
Пусть a — длина двух равных сторон равнобедренного треугольника, b — длина третьей стороны, 

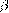 — соответствующие углы, R — радиус описанной окружности, r — радиус вписанной окружности.
— соответствующие углы, R — радиус описанной окружности, r — радиус вписанной окружности.
Соотношения для сторон:
- a =2 R
 sin
sin 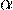
 b =2 R
b =2 R  sin
sin 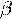 (теорема синусов);
(теорема синусов); - a = b 2 cos
 (следствие теоремы косинусов);
(следствие теоремы косинусов); - b = a
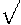 2(1− cos
2(1− cos 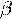 ) (следствие теоремы косинусов);
) (следствие теоремы косинусов); - b =2 a
 cos
cos 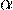 (теорема о проекциях).
(теорема о проекциях).
Соотношения для углов:
-
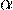 =2
=2  −
− 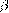 ;
; -
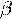 =
= 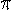 −2
−2 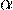 ;
; -
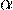 = arcsina 2 R
= arcsina 2 R 
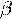 = arcsinb 2 R.
= arcsinb 2 R.
Соотношения для периметра:
- P = 2a + b (по определению);
- P =2 R (2 sin
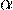 + sin
+ sin 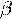 ).
).
Соотношения для площади:
- S =21 a 2 sin
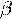 =21 absin
=21 absin 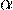 ;
; - S =21 b
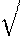 a 2−41 b 2 (формула Герона).
a 2−41 b 2 (формула Герона).
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Равносторонний треугольник
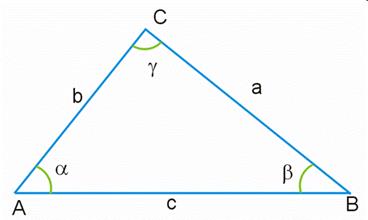
| Треугольник — простейший многоугольник, имеющий 3 вершины и 3 стороны; часть плоскости, ограниченная тремя точками, не лежащими на одной прямой, и тремя отрезками, попарно соединяющими эти точки.
Вершины треугольника обычно обозначаются заглавными латинскими буквами (A, B, C), величины углов при соответственных вершинах — греческими буквами (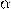  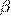  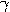 ), а длины противоположных сторон — прописными латинскими буквами (a, b, c). ), а длины противоположных сторон — прописными латинскими буквами (a, b, c).
|
Правильный треугольник или равносторонний треугольник — правильный многоугольник с тремя сторонами. Все стороны равны между собой, и все углы равны 60° (или 3  ).
).
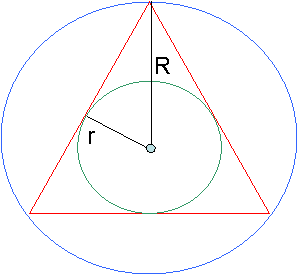
| Пусть t — сторона правильного треугольника, R — радиус описанной окружности, r — радиус вписанной окружности.
- Радиус вписанной окружности правильного треугольника, выраженный через его сторону r =6
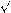 3 3  t. t. - Радиус описанной окружности правильного треугольника, выраженный через его сторону R =3
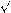 3 3  t. t. - Периметр правильного треугольника равен P =3 t =3
 3 R =6 3 R =6  3 r. 3 r. - Высота правильного треугольника: h =2
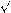 3 t. 3 t. - Площадь правильного треугольника рассчитывается по формулам: S =4
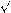 3 t 2=43 3 t 2=43 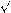 3 R 2=3 3 R 2=3  3 r 2. 3 r 2. |

 c
c  A (или формула b 2= a 2+ c 2−2 a
A (или формула b 2= a 2+ c 2−2 a  cb 2+ c 2− a 2; cos
cb 2+ c 2− a 2; cos  A = bsin
A = bsin 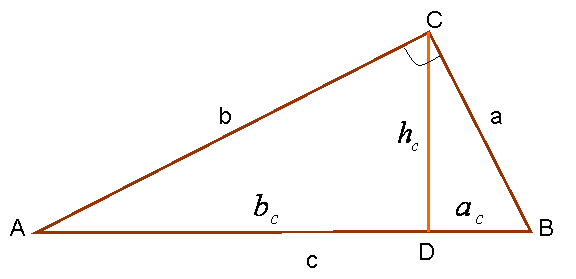
 ac
ac  ac
ac  b =
b = 




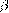 — соответствующие углы, R — радиус описанной окружности, r — радиус вписанной окружности.
— соответствующие углы, R — радиус описанной окружности, r — радиус вписанной окружности. sin
sin 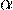
 b =2 R
b =2 R 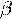 (теорема синусов);
(теорема синусов);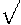 2(1− cos
2(1− cos  −
− 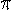 −2
−2 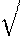 a 2−41 b 2 (формула Герона).
a 2−41 b 2 (формула Герона).
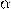
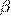
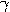 ), а длины противоположных сторон — прописными латинскими буквами (a, b, c).
), а длины противоположных сторон — прописными латинскими буквами (a, b, c).
 ).
).
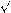 3
3 


