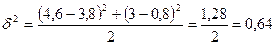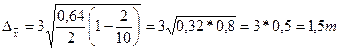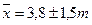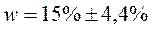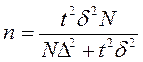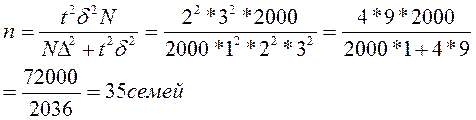Собственно – случайная.
Это такая, при которой отбор единиц в выборочную совокупность производится непосредственно из всей массы единиц генеральной совокупности. При этом количество отобранных единиц обычно определяется исходя из принятой доли выборки. Для выборки есть отношение числа единиц выборочной совокупности и к численности единиц генеральной совокупности N.
Так при 5% выборке из партии товара в 2000 единиц численность выборки n составляет 100 ед. ( ( Важное условие собственно случайной выборки в том, что каждой единице генеральной совокупности предоставляется равная возможность попасть в выборочную совокупность. При случайном отборе предельная ошибка выборки для средней
для доли
n- численность выборки t- коэффициент доверия, который определяется по таблице значений интегральной функции Лапласа при заданной вероятности P. P=0.683 t=1 P=0.954 t=2 P=0.997 t=3 При бесповторном отборе предельная ошибка выборки определяется по формуле для средней
где N –численность генеральной совокупности доли
Пример Для определения зольности угля в порядке случайной выборке было обследовано 100 проб угля. В результате обследования установлено, что средняя зольность угля в выборке 16%, Решение Средняя зольность
определяем предельную ошибку выборки
при p=0.954 t=2
доля угля с зольностью >20%
выборочная доля определяется
где m- доля единиц, обладающих признаком
ошибку выборки для доли
С вероятностью 0,954 можно утверждать, что доля угля с зольностью более 20% в месторождении будет находиться в пределах P= 10%+(-)6% или Механическая выборка. Это разновидность собственно – случайной. В этом случае вся генеральная совокупность делится на n равных частей и затем из каждой части отбирается одна единица.
Все единицы генеральной совокупности должны располагаться в определенном порядке. При этом по отношению к изучаемому показателю единицы генеральной совокупности могут быть упорядочены по существенному, второстепенному или нейтральному признаку. При этом из каждой группы должна отбираться та единица, которая находится в середине каждой группы. Это позволяет избежать систематической ошибки выборки. Применяют: при обследовании покупателей в магазинах, посетителей в поликлиниках, каждый 5,4,3 и т.д Пример механическая выборка Для определения среднего срока пользования краткосрочным кредитом в банке будет произведена 5% механическая выборка, в которую попало 100 счетов. В результате обследования установлено, что средний срок пользования краткосрочным кредитом 30 дней при Решение Ошибка выборки
т.е. с вероятность 0,954 можно утверждать, что срок пользования кредитом колеблется 1 в пределах 30дн.+(-)2дня, т.е. 2 доли кредитов со сроком > 60дней.
выборочная доля составит
ошибку доли определим
с вероятностью 0,954 можно утверждать, что доля кредитов в банке со сроком пользования >60дней будет находиться в пределах Типическая выборка. Генеральная совокупность разделяется на однородные типические группы. Затем из каждой типической группы собственно-случайной или механической выборкой производится индивидуальный отбор единиц в выборочную совокупность Например: пр. тр. работников, состоящих из отдельных групп по квалификации. Важная особенность – дает более точные результаты по сравнению с другими, т.к. в выборке участвует типологическая единица. Отбор единиц наблюдения в выборочную совокупность производится различными методами. Рассмотрим типическую выборку с пропорциональным отбором внутри типических групп. Объем выборки из типической группы при отборе пропорциональном численности типических групп, определяется по формуле
где
Предельная ошибка выборочной средней и доли при бесповторном случайном и механическом способе отбора внутри типических групп рассчитывается по формулам
где Пример: типическая выборка Для определения среднего возраста мужчин, вступающих в брак, в районе была произведена 5% выборка с отбором единиц пропорционально численности типических групп Внутри групп применялся механический отбор
С вероятностью 0,954 определить пределы в которых будут находиться средний возраст мужчин, вступивших в брак, и долю мужчин, вступивших в брак вторично. Решение
средний возраст вступают в брак мужчины в выборочной совокупности
предельная ошибка выборки
с вероятностью 0,954 можно утверждать, что средний возраст мужчин, вступающих в брак, будет находиться в пределах
для мужчин, вступающих во второй брак находиться в пределах
выборочная доля определяется
выборочная дисперсия альтернативного признака равна
с вероятностью 0,954 можно утверждать, что доля вступающих в брак во второй раз находится в пределах
Серийная выборка. При серийной выборке совокупность делят на одинаковые по объему группы – серии. Выборочную совокупность отбираются серии. Внутри серий производится сплошное наблюдение единиц, попавших в серию. При бесповторном отборе
где
где
R- число серий генеральной совокупности r- число отобранных серий Пример: в цехе 10 бригад с целью изучения их производительности труда будет осуществлена 20% серийная выборка, в которую попали 2 бригады. В результате обследования установлено, что Решения
выборочная средняя серийной выборки определяется по формуле
с вероятностью 0,997 можно утверждать, что средняя выработка рабочих цеха находится в пределах Пример. На складе готовой продукции цеха находятся 200 ящиков деталей по 40 штук в каждом ящике. Для проверки качества готовой продукции будет произведена 10% серийная выборка. В результате выборки установлено, что для бракованных деталей составляет 15%. Дисперсия серийной выборки равна 0,0049. С вероятностью 0,997 определить пределы, в которых находится доля бракованной продукции в партии ящиков Решение Доля бракованных деталей будет находиться в пределах
определим предельную ошибку выборки для доли по формуле
с вероятностью 0,997 можно утверждать, что доля бракованных деталей в партии находится в пределах
В практике проектирования выборочного наблюдения возникает потребность нахождении численности выборки, которая необходима для обеспечения определенной точности расчета генеральных характеристик - средней и доли. Предельная ошибка выборки, вероятность ее появления и вариация признака предварительно известны. При случайном повторном отборе численность выборки определяется по формуле
при случайном бесповторном и механическом отборе численность выборки
для типической выборки
для серийной выборки
Пример в районе проживает 2000 семей.
Предполагается провести их выборочное обследование методом случайного бесповторного отбора для нахождения среднего размера семьи. Определить необходимую численность выборки при условии, что с вероятностью 0,954 ошибка выборки не превысит 1 человека при среднем квадратическом отклонении 3 человека. Решение
Пример. В городе проживает 10тыс. семей. С помощью механической выборки предлагается определить долю семей с тремя детьми и более. Какова должна быть численность выборки, чтобы с вероятностью Р=0,954 ошибка выборки не превышала 0,02, если на основе предыдущих обследований известно, что дисперсия равна 0,02? Решение.
|


 ), а при 20% выборке она составит 400 ед.
), а при 20% выборке она составит 400 ед. )
) равна
равна

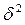 - дисперсия выборочной совокупности
- дисперсия выборочной совокупности

 = 5%. В 10-ти пробах зольность угля составила >20% с вероятностью 0,954 определить пределы, в которых будет находиться средняя зольность угля в месторождении и доля угля с зольность >20%
= 5%. В 10-ти пробах зольность угля составила >20% с вероятностью 0,954 определить пределы, в которых будет находиться средняя зольность угля в месторождении и доля угля с зольность >20%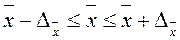
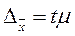
 2*0.5=1%
2*0.5=1%
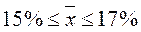

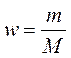
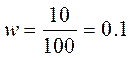
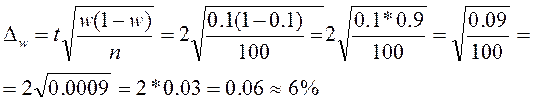

 9дней в 5-ти счетах срок пользования кредитом > 60 дней.
9дней в 5-ти счетах срок пользования кредитом > 60 дней.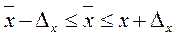
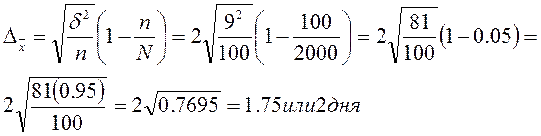

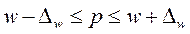
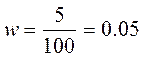
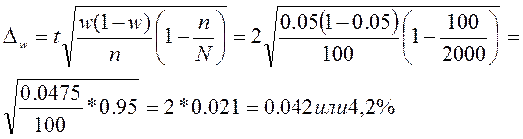

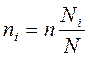
 = V выборки из типической группы
= V выборки из типической группы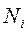 = V типической группы.
= V типической группы.
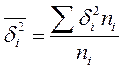

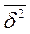 =дисперсия выборочной совокупности
=дисперсия выборочной совокупности

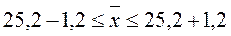




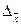 и
и  определяют по формуле
определяют по формуле
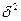 - межсерийная дисперсия
- межсерийная дисперсия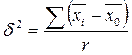
 выборочная средняя серии
выборочная средняя серии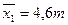
 с вероятностью 0,997 определить пределы, в которых будет находиться средняя выработка рабочих цеха.
с вероятностью 0,997 определить пределы, в которых будет находиться средняя выработка рабочих цеха.