Фундаментальное решение уравнения теплопроводности; его физический смысл.
Нестационарное уравнение теплопроводности в неподвижной среде в декартовой системе координат имеет вид:
Рассмотрим безграничное пространство, заполненное однородной неподвижной средой с плотностью r, теплоемкостью c и коэффициентом температуропроводности a. Пусть в этом пространстве в точке с координатами x', y', z' в момент времени t' сработал (включился и сразу же выключился) мгновенный источник тепла, выделивший количество тепла, равное Q. Тогда температура в любой точке с координатами x, y, z в любой момент времени t > t' может быть определена по формуле
Функция (2) ввиду ее чрезвычайной важности для приложений называется фундаментальным решением уравнения теплопроводности. В том, что эта функция является решением уравнения теплопроводности (1), проще всего убедиться непосредственной проверкой. Продифференцируем фундаментальное решение один раз по t и дважды по x, y, z:
Подставляя эти формулы в уравнение (1), убеждаемся, что при t > t' получается тождество. На первый взгляд может показаться, что практическая польза от фундаментального решения невелика, т.к. мгновенных точечных источников в природе и в технике не существует; любой реальный источник имеет конечные размеры и действует в течение конечного промежутка времени. Однако всегда можно мысленно разбить источник тепла на отдельные элементы, настолько малые, чтобы их можно было считать точечными, и, используя принцип суперпозиции, сложить температуры, создаваемые этими элементами (другими словами, проинтегрировать фундаментальное решение по координатам x', y', z' в пределах реальных размеров источника). Аналогично, отрезок времени, в течение которого действовал источник, можно разбить на множество бесконечно малых интервалов dt' и проинтегрировать фундаментальное решение по t' от момента включения до момента выключения источника. При этом можно учесть, что различные элементы источника могут иметь различную мощность, которая к тому же может меняться со временем, т.е. решить множество практически важных задач. Если источники тепла имеют сложную форму, и (или) их мощность меняется сложным образом, так что получить аналитическое решение не удается, можно применить методы численного интегрирования. Простейшие примеры применения этих идей приведены ниже. Кроме того, в некоторых случаях, когда мощный источник тепла действовал непродолжительное время, на расстояниях, много больших, чем размеры источника, можно непосредственно использовать формулу (2). В качестве примера можно назвать подземный взрыв (обычный или ядерный небольшой мощности), произведенный на большой глубине. Рассмотрим некоторые свойства фундаментального решения. Если начало координат поместить в точку (x', y', z') а отсчет времени начать с момента t', то вид формулы (2) значительно упрощается:
Производная обратится в нуль, когда величина, стоящая в скобках, будет равна нулю, т.е. в момент времени t1 = r2/(6a). В этот момент температура в точке, находящейся на расстоянии r от мгновенного точечного источника достигает максимума.
|

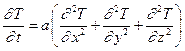 . (1)
. (1)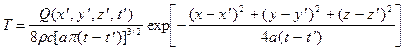 . (2)
. (2)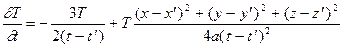 ,
,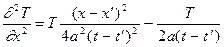 ,
, 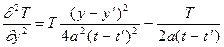 ,
,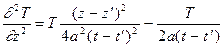 .
.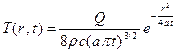 , (3)
, (3) где r2 = x2 + y2 + z2 - квадрат расстояния от источника (от начала координат) до точки наблюдения. Если зафиксировать ряд моментов времени 0 < t1 < t2 < t3 и построить графики зависимости T(r), то получатся кривые, вид которых изображен на рисунке. Как видно из этого рисунка, температура максимальна в начале координат (в точке, где находился источник тепла), и с увеличением r монотонно убывает. Чем ближе момент времени t к моменту срабатывания источника (к началу отсчета времени), тем выше и уже пик кривой T(r). С течением времени тепло постепенно распространяется во все стороны, но если в любой фиксированный момент времени проинтегрировать rcT по всему пространству, то получится величина, равная Q, как и должно быть по закону сохранения энергии.
где r2 = x2 + y2 + z2 - квадрат расстояния от источника (от начала координат) до точки наблюдения. Если зафиксировать ряд моментов времени 0 < t1 < t2 < t3 и построить графики зависимости T(r), то получатся кривые, вид которых изображен на рисунке. Как видно из этого рисунка, температура максимальна в начале координат (в точке, где находился источник тепла), и с увеличением r монотонно убывает. Чем ближе момент времени t к моменту срабатывания источника (к началу отсчета времени), тем выше и уже пик кривой T(r). С течением времени тепло постепенно распространяется во все стороны, но если в любой фиксированный момент времени проинтегрировать rcT по всему пространству, то получится величина, равная Q, как и должно быть по закону сохранения энергии. Если теперь зафиксировать некоторую точку на расстоянии r от источника и проследить за изменением температуры в этой точке со временем, то получится зависимость T(t), вид которой изображен на рисунке. Максимум температуры достигается в некоторый момент времени t1, который можно определить, приравняв производную ¶T/¶t нулю:
Если теперь зафиксировать некоторую точку на расстоянии r от источника и проследить за изменением температуры в этой точке со временем, то получится зависимость T(t), вид которой изображен на рисунке. Максимум температуры достигается в некоторый момент времени t1, который можно определить, приравняв производную ¶T/¶t нулю: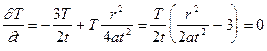 .
.


