Включение трансформатора в сеть
На первичную обмотку трансформатора в момент времени t =0 подается синусоидальное напряжение
а вторичная обмотка трансформатора разомкнута (рис. 1.16, а).
а) б) Рис. 1.16. Включение трансформатора в сеть (а) и КЗ во вторичной обмотке (б)
Так как в трансформаторе имеется стальной сердечник, то индуктивность обмотки является величиной переменной, зависящей от тока, поэтому в уравнении равновесия напряжений вместо тока i следует записать потокосцепление обмотки Y= L 1 i:
где Ψ – полное потокосцепление первичной обмотки; L 1, R 1 – индуктивность и активное сопротивление первичной обмотки. Между L 1 и i имеется зависимость L 1(i), определяемая нелинейной характеристикой намагничивания стали сердечника, поэтому дифференциальное уравнение (1.6) является нелинейным и решение может быть только приближенным. Чтобы перевести это нелинейное уравнение в линейный вид, удобный для приближенного решения, следует выразить второй член через потокосцепление Ψ. Это можно сделать, так как для трансформаторов w L 1>> R 1 и основное падение напряжения имеет место на индуктивном, а не на активном сопротивлении. Следовательно, второй член в дифференциальном уравнении (1.6) имеет малое значение и его можно представить приближенно, выражая ток через индуктивность L 1, которая принимается постоянной величиной, соответствующей прямолинейному участку характеристики намагничивания стали, т. е. i = Ψ/ L. Тогда
Включение трансформатора может произойти в любой момент времени, т. е. при любом значении угла a от нуля до Приближенное решение дифференциального уравнения (1.6) можно получить в виде
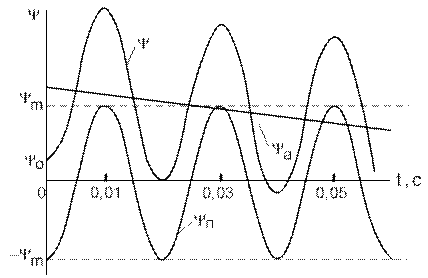
где Т 1= Ym – амплитудное значение потокосцепления. Видно, что решение состоит из двух составляющих – периодической Yп и апериодической Yа, затухающей с постоянной времени Т 1 (рис. 1.17).
Рис. 1.17. Изменение потокосцепления Y первичной обмотки трансформатора
Изменение тока в первичной обмотке трансформатора с учётом характеристики намагничивания можно определить графически (рис. 1.18). Построение начинается с вычерчивания зависимости Ψ(t) в первом квадранте и кривой намагничивания сердечника трансформатора Ψ(i) во втором и четвертом квадрантах. Графическое построение зависимости i (t) на примере двух точек 1 и 2 показано на рис. 1.17. Из рис. 1.18 видно, что вследствие насыщения стали сердечника трансформатора максимальный бросок тока намагничивания i у может значительно превосходить ток намагничивания нормального режима.
Рис. 1.18. Графическое определение изменения тока в первичной обмотке трансформатора
|

 ,
,
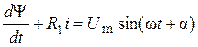 , (1.6)
, (1.6)
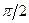 . Из п. 1.1.1 известно, что максимальное значение тока в активно-индуктивной цепи, включаемой на синусоидальное напряжение, наступает при прохождении напряжения через нулевое значение, т. е. при a=0. Именно этот случай и рассмотрим ниже.
. Из п. 1.1.1 известно, что максимальное значение тока в активно-индуктивной цепи, включаемой на синусоидальное напряжение, наступает при прохождении напряжения через нулевое значение, т. е. при a=0. Именно этот случай и рассмотрим ниже. ,
,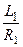 – постоянная времени первичной обмотки трансформатора;
– постоянная времени первичной обмотки трансформатора;