Статическая устойчивость асинхронных двигателей
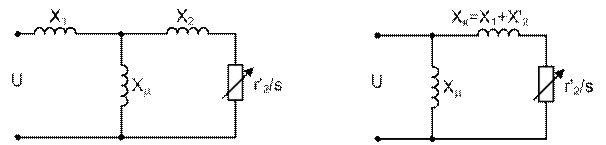
Схема замещения асинхронного двигателя приведена на рис. 2.9, а. Для определения потребляемой асинхронным двигателем активной и реактивной мощности воспользуемся упрощенной схемой замещения (рис. 2.9, б), в которой ветвь намагничивания, потребляющая относительно небольшой ток, вынесена на вход двигателя.
а) б) Рис. 2.9. Схемы замещение асинхронного двигателя, питающегося от мощной системы: а – исходная; б – упрощенная
На упрощенной схеме замещения двигателя приняты следующие обозначения: х к – сумма индуктивного сопротивления обмотки статора х 1 и приведенного к статору индуктивного сопротивления обмотки ротора х’ 2; х μ – сопротивление ветви намагничивания; r’ 2 – активное сопротивление ротора, приведенное к обмотке статора, при стоящем двигателе; s = w0 и w – синхронная частота вращения (частота вращения поля статора) и реальная частота вращения ротора, 1/c; n 0 и n – механическая номинальная и реальная скорости вращения, об/мин. Для схемы замещения рис. 2.9, б активная мощность, потребляемая двигателем, определяется выражением
Определим максимум этой характеристики, для чего приравняем к нулю производную от мощности по скольжению
где s кр – скольжение, соответствующее максимальной мощности (критическое скольжение). Подставляя выражения для P maxи s кр в (2.9), получим известную из теории электрических машин формулу Клосса:
К сожалению, эта формула, полученная в первой половине ХХ века, справедлива для двигателей с однослойной обмоткой, которые сейчас практически не выпускаются. Для современных двигателей более экономичной и, следовательно, более сложной конструкции в эту формулу необходимо вводить ряд поправочных коэффициентов. Реактивная мощность, потребляемая двигателем, определяется выражением
Таким образом, суммарная реактивная мощность, потребляемая двигателем из сети, состоит из двух составляющих: первая Qs отражает зависимость реактивной мощности рассеяния от напряжения и скольжения, вторая Q μ – зависимость реактивной мощности намагничивания от напряжения. Мощность Qs при уменьшении напряжения увеличивается за счет более заметного увеличения скольжения. При скольжении больше критического (s > s кр » 0,2), что имеет место при напряжении (0,6-0,7) U ном, двигатель интенсивно затормаживается и останавливается (опрокидывается). Мощность Q μ при изменении напряжения изменяется по квадратичной зависимости (см. рис. 2.10).
Рис. 2.10. Характеристикиреактивной мощности асинхронногодвигателя
На основании (2.9) или (2.10) построим характеристику мощности (момента) асинхронного двигателя (рис. 2.11). Рассмотрим случай, когда момент сопротивления механизма не зависит от скорости вращения двигателя. В этом случае характеристика механизма будет изображаться прямой, параллельной оси абсцисс. Способность двигателя самостоятельно возвращаться к исходному режиму работы после малых возмущений называют статической устойчивостью двигателя. Определим практические критерии статической устойчивости двигательной нагрузки. Рассмотрим сначала характеристики системы асинхронный двигатель- механизм. В этой системе вращающий электромагнитный момент создаётся двигателем, а механический момент сопротивления – приводимым в движение механизмом. Точки пересечения характеристик двигателя и механизма являются точками, где возможен установившийся режим, так как действующие на валу агрегата моменты уравновешены. Однако только в одной из этих точек режим системы будет устойчив.
Рис. 2.11. Режимы работы асинхронного двигателя: а – устойчивый; б – неустойчивый
Предположим, что при работе системы в точке а двигатель по какой-либо причине притормозился, то есть произошло небольшое увеличение скольжения. Тогда электромагнитная мощность возрастёт, двигатель ускорится, скольжение уменьшится, и система вернется к режиму в точке а. Иное положение создаётся при работе в точке б. Здесь любое малое возмущение вызовет либо торможение вплоть до остановки, либо переход в режим, соответствующий точке а. Из всех режимов, лежащих левее и ниже точки а и левее и выше точки б, двигатель будет стремиться перейти в точку устойчивого равновесия а. Из режимов, лежащих правее и ниже точки б, двигатель будет стремиться в сторону увеличения скольжения (уменьшения скорости) вплоть до полной остановки. Отсюда можно сделать вывод, как и в случае синхронного двигателя, что все режимы, соответствующие точкам, лежащим на восходящей части характеристики двигателя, могут быть реализованы, все режимы на нисходящей части неустойчивы. Условие устойчивой работы можно записать в виде
При Таким образом, режим работы асинхронного двигателя устойчив, если производная от мощности двигателя по скольжению больше нуля. Этот критерий удобно применять для анализа режимов, связанных с увеличением нагрузки двигателя. Однако нарушение статической устойчивости может произойти и при снижении напряжения питания. Характеристики асинхронного двигателя при разных величинах напряжения на его зажимах показаны на рис. 2.12. Приводимый во вращение механизм имеет не зависящую от скорости вращения характеристику.
Рис. 2.12. Характеристики мощности асинхронного двигателя и механизма
При снижении напряжения на зажимах двигателя увеличивается скольжение,двигатель начинает тормозиться, но мощность, развиваемая двигателем, остается неизменной до тех пор, пока максимальная электромагнитная мощность не станет равной мощности механизма (напряжение, соответствующее такому режиму, называют критическим U кp). Как только это случится, двигатель будет тормозиться до полной остановки (опрокинется), поскольку мощность двигателя окажется меньше мощности механизма. Условие нарушения устойчивой работы можно в этом случае записать в виде (см. рис. 2.10)
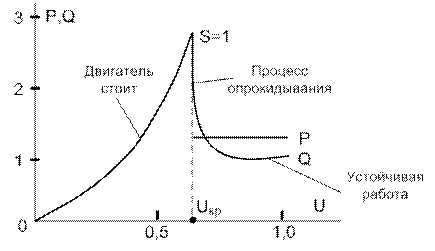
В соответствии с (2.9) зависимость P(U) имеет квадратичный характер, поэтому снижение максимума активной мощности двигателя при снижении напряжения превосходит в относительных единицах снижение напряжения. Изменения активной и реактивной мощностей асинхронного двигателя при снижении напряжения на его зажимах хорошо видны на рис. 2.13. Активная мощность не изменяетсявплоть до момента опрокидывания (при этом незначительно возрастает скольжение). Реактивная мощность в процессе опрокидывания двигателя резко увеличивается. После остановки двигателя суммарная реактивная мощность при снижении напряжения уменьшается.
Рис. 2.13. Изменения активной и реактивной мощностей асинхронного двигателя при изменении напряжения
Рассмотрим режимы работы двигателя на границе устойчивости. При равенстве максимальной мощности двигателя P мах и мощности механизма Р о происходит опрокидывание двигателей, т. е. нарушение их устойчивой работы. Этот процесс начинается при равенстве нулю производной Как было показано выше,
При критическом напряжении Р max= Р 0. Тогда
|

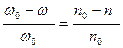 – скольжение ротора относительно поля статора;
– скольжение ротора относительно поля статора;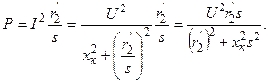 (2.9)
(2.9)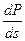 =0. Проведя необходимые преобразования, получим
=0. Проведя необходимые преобразования, получим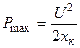 при
при 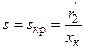 , (2.9 a)
, (2.9 a)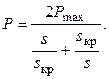 (2.10)
(2.10)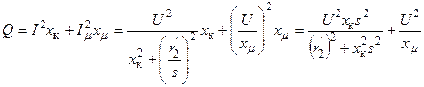
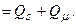 (2.11)
(2.11)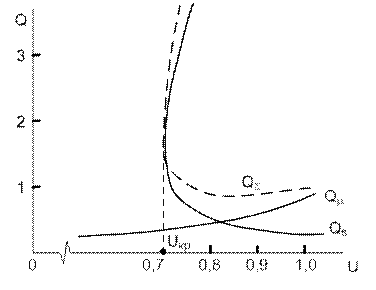

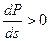 .
. имеем граничный режим, при
имеем граничный режим, при  режим работы будет неустойчивым.
режим работы будет неустойчивым.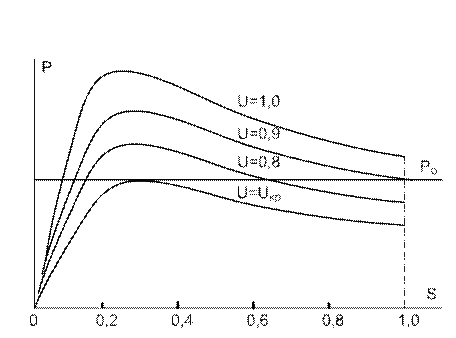
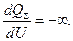
 .
.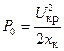 , откуда
, откуда 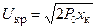 .
.


