Предельное время отключения КЗ
Для практических целей важнее знать не угол dоткл.пр, а время, за которое он будет достигнут. Для схемы рис. 2.5, а рассмотрим трехфазное КЗ в начале линии, для которого Р m2=0 (рис. 2.7). Дифференциальное уравнение движения ротора было получено выше и для трехфазного КЗ имеет вид
Перепишем это уравнение в виде
Взяв интеграл от левой и правой частей, получим
При t =0 относительная скорость ротора w=0 и, следовательно, с1=0.
Рис. 2.7. Трехфазное КЗ в начале линии
Проинтегрировав еще раз последнее выражение, получим
Постоянная интегрирования с2 определяется из условий d=d0, с2=d0 при t =0. Окончательно зависимость угла от времени будет иметь вид
Возрастание угла происходит по квадратичной параболе, а время, отвечающее какому-либо значению угла d, найдется из последнего выражения как
Предельный угол отключения трехфазного КЗ может быть определен из выражения (2.2), записанного для случая Р mII=0, cos dоткл. пр.= Предельное время отключения трехфазного КЗ определится из формулы (2.3):
|

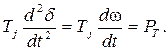
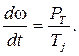




 . (2.3)
. (2.3)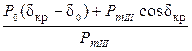 .
.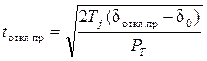 .
.


