Решение уравнения движения ротора
Дифференциальное уравнение движения ротора синхронной машины
решается методами численного интегрирования, одним из которых является метод последовательных интервалов. В соответствии с этим методом весь процесс движения ротора разбивается на ряд интервалов времени D t и для каждого интервала последовательно вычисляется приращение угла Dd. В нормальном установившемся режиме имеет место равенство Р Т= Р msind и угол d остается неизмененным. В момент КЗ отдаваемая генератором мощность Р msind падает, и на валу турбина-генератор возникает некоторый избыток мощности D Р (0), и ротор машины получает ускорение
Здесь принято, что при небольших изменениях скорости приращения момента и мощности в относительных единицах равны между собой. Для малого интервала времени D t можно допустить, что избыток мощности D Р (0) в течение этого интервала остается неизмененным. Интегрируя выражение (2.4), получим в конце первого интервала
где D V – приращение относительной скорости ротора. Относительная скорость ротора в начальный момент КЗ равна нулю (с1=0). Относительная скорость ротора в конце первого интервала равна D V (1). При t =0 угол d=d0, поэтому с2=d0. Приращение угла на первом интервале с учетом (2.5) составит Dd(1)= a(0) Здесь угол и время представлены в радианах. В практических расчетах угол выражают в градусах, а время – в секундах: d(град) = где w0 – синхронная скорость. Используя последние выражения и учитывая, что Т j(c)= d(1)=d0+ где К = Ускорение, создаваемое во втором интервале, пропорционально избытку мощности в конце первого интервала D Р (1). При вычислении приращения угла в течение второго интервала необходимо учесть то, что, кроме действующего в этом интервале ускорения a(1) ротор уже имеет в начале второго интервала скорость V (1): Dd(2)= V (1)D t + где D Р (1)= Р 0 – Р m sind(1). Значение скорости V (1) неточное, так как ускорение a(0) не является постоянным в течение первого интервала времени. По аналогии с (2.5) вычислим ускорение к концу первого интервала:
и предположим, что на первом интервале действует среднее ускорение a(0)ср= Тогда относительная скорость ротора будет выражена формулой V (1) = Подставляя это уравнение в (2.7), получим Dd(2) = или Dd(2) =Dd(1) + К D Р (1). Приращение угла на последующих интервалах рассчитывается аналогично: Dd(n) =Dd(n-1) + К D Р (n-1). Если на некотором интервале времени D t iпроисходит отключение КЗ, то избыток мощности скачкообразно меняется от некоторой величины D Р¢;(i-1) до величины D Р″; (i-1). Приращение угла на первом интервале после отключения КЗ определится как Dd(i) =Dd(i-1) + К Расчет методом последовательных интервалов ведется до тех пор, пока угол d не начнет уменьшаться, либо не будет ясно, что этот угол неограниченно растет и динамическая устойчивость нарушается.
|

 (2.4)
(2.4)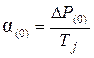 . (2.5)
. (2.5)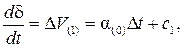 d(1)=a(0)
d(1)=a(0) 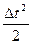 +с2,
+с2,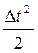 =
= 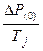
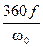 d(рад), t (c)=
d(рад), t (c)=  ,
,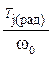 , получим
, получим d0+ K
d0+ K  ,
,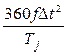 . (2.6)
. (2.6)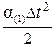 = V (1)Dt + К
= V (1)Dt + К  , (2.7)
, (2.7)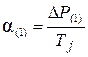 ,
,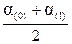 .
. D t 2 +
D t 2 +  =
= 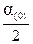 D t 2 + a(1)D t 2,
D t 2 + a(1)D t 2, . (2.8)
. (2.8)


