Понятие о динамической устойчивости системы
Предметом изучения динамической устойчивости является изучение поведения системы после больших возмущений, в частности после КЗ. Для выяснения принципиальных положений динамической устойчивости рассмотрим переходный процесс, вызванный КЗ на одной из линий электропередачи, соединяющих электростанцию с системой бесконечной мощности, с последующим отключением поврежденной линии (рис.2.5). Для более общего случая будем считать, что КЗ несимметричное. Чтобы проследить изменение электромагнитной мощности генератора во время переходного процесса, необходимо построить моментно-угловые характеристики мощности для трёх режимов: - нормального (исходного); - аварийного (во время КЗ); - послеаварийного (при отключённой линии).
Рис. 2.5. Принципиальная схема электропередачи (а) и схемы замещения для нормального (б), аварийного (в) и послеаварийного (г) режимов
С этой целью составим схемы замещения электропередачи для перечисленных режимов (рис. 2.5), замещая генератор переходной ЭДС Е' за переходным сопротивлением Х ¢d, и определим амплитуды характеристик для каждого режима. Амплитуда характеристики мощности для исходного режима
где Амплитуда характеристики мощности для режима КЗ
где D Х – шунт несимметричного КЗ, величина которого зависит от вида КЗ (см. табл. 1.2). Сопротивление Х II определено как сопротивление стороны треугольника, связывающее генератор и систему, после преобразования звезды (рис. 2.5, в) в треугольник. Амплитуда характеристики мощности для послеаварийного режима
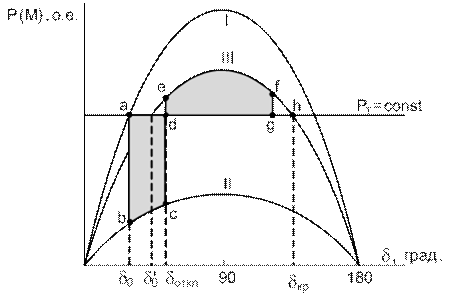
где На рис. 2.6 показаны характеристики I, II, III указанных выше режимов. Рассмотрим, как меняется электромагнитная мощность генератора при переходах от одного режима к другому. В момент, соответствующий началу КЗ, происходит переход из точки а характеристики нормального режима в точку b характеристики аварийного режима, так как вследствие инерции ротора угол δмгновенно измениться не может. В результате на валу системы турбина-генератор возникает избыточный ускоряющий момент, обусловленный разностью моментов (мощностей) турбины РТ и генератора Р. Мощность турбины принимается неизменной за всё время переходного процесса РТ = const, так как регулятор скорости не успевает за это время изменить мощность, развиваемую турбиной.
Рис. 2.6. Моментно-угловые характеристики в нормальном (I), аварийном (II) и послеаварийном (III) режимах
Под влиянием ускоряющего момента ротор генератора начнет перемещаться относительно вектора напряжения приёмной системы, угол δ будет увеличиваться. Этому процессу соответствует движение из точки b в точку c. После отключения КЗ электромагнитная мощность становится больше мощности турбины и на валу агрегата появляется избыточный тормозящий момент (точка e). Несмотря на это, ротор ещё некоторое время будет перемещаться в сторону увеличения угла δ, пока не израсходуется запасенная им за время КЗ кинетическая энергия (точка f). Если эта энергия будет израсходована до достижения ротором генератора точки h, ротор начнет перемещаться в обратном направлении и после нескольких колебаний перейдёт в новый установившийся режим с углом δ¢0.Если же ротор пройдёт точку h, то избыточный момент вновь станет ускоряющим и генератор выйдет из синхронизма. В первом случае считают, что система динамически устойчива, во втором – неустойчива. Приведенный на рис. 2.6 метод оценки динамической устойчивости электроэнергетической системы получил название метода площадей. На рис. 2.6 площадь abcd эквивалентна энергии ускоряющей ротор (площадь ускорения ротора), а площ адь defg эквивалентна энергии, тормозящей ротор (площадь торможения ротора). Для рассматриваемого случая максимально возможная энергия торможения эквивалентна площади defh. Таким образом, если возможная площадь торможения будет больше площади ускорения, то система будет динамически устойчива.
|

 а) б)
а) б) в) г)
в) г) ,
, .
.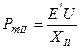 ,
,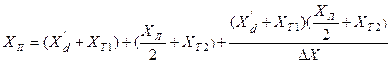 ;
;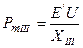 ,
, .
.