Статическая устойчивость простейшей системы. Под простейшей системой понимается такая, в которой синхронная машина G связана с системой С через трансформаторы и линии (рис
Под простейшей системой понимается такая, в которой синхронная машина G связана с системой С через трансформаторы и линии (рис. 2.1, а). Принимается, что: - суммарная мощность генераторов системы во много раз превышает мощность синхронной машины G; это позволяет считать напряжение на шинах системы неизменным (U= const); - скорость вращения постоянна и равна номинальной; это позволяет считать, что в относительных единицах момент равен активной мощности. Синхронная машина может работать в трех режимах: - генераторном; - двигательном; - синхронного компенсатора (синхронного двигателя без нагрузки на валу).
На рис. 2.1, б схематично представлены турбина и генератор. Турбина приводится во вращение энергоносителем (паром, водой, газом и др.). Вращающий момент турбины зависит от количества энергоносителя. В нормальном установившемся режиме вращающий момент турбины постоянный. Турбина вращает генератор. Величина активной мощности, выдаваемой генератором в систему, определяется только количеством энергоносителя, подаваемого в турбину.
б) г)
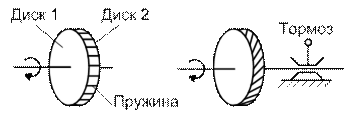
Рис. 2.1. Оценка статической устойчивости простейшей системы: а – принципиальная схема системы; б – блок турбина-генератор; в – векторная диаграмма генератора; г – схема замещения системы; д – механический аналог блока турбина-генератор
Для получения характеристики мощности построена векторная диаграмма электропередачи (рис. 2.1, в). При её построении полный вектор тока I разложен на действительную I a и мнимую I p составляющие. Как следует из схемы замещения передачи (рис. 2.1, г), результирующее сопротивлениепередачи Х dS = Х d + Х Т1 + Х L1 || Х L1+ Х Т2. ЭДС синхронной машины Е есть сумма векторов напряжения системы U и падения напряжения IХ dS на результирующем сопротивлении.
Из векторной диаграммы следует, что I a Х dS = Е sin d, где d – угол между ЭДС синхронной машины Е и напряжением системы U. Умножая обе части этого равенства на U / Х dS, получим
где Р – активная мощность, выдаваемая генератором. Зависимость (2.1) имеет синусоидальный характер и называется характеристикой мощности, или моментно-угловой характеристикой, синхронной машины (мощность и момент синхронной машины пропорциональны, а в относительных единицах равны). При неизменных ЭДС синхронной машины Е, напряжении системы U и сопротивлении x dS угол d определяется: - для генератора только выдаваемой активной мощностью, - для двигателя только потребляемой активной мощностью. Мощность, выдаваемая генератором, имеет максимум Наглядной иллюстрацией зависимости мощности (момента) турбины от угла сдвига δ является система двух дисков, соединенных пружинами (рис. 2.1, д). В режиме холостого хода (без учета трения) ведущий диск (поле ротора, связанного с турбиной) и ведомый диск (поле статора) не образуют угла сдвига относительно друг друга. При появлении тормозящего момента (нагрузки генератора) угол сдвига между дисками будет тем больше, чем больше тормозящий момент. Очевидно, что при увеличении тормозящего момента может произойти проворот одного диска относительно другого, что является нарушением устойчивости рассматриваемой системы.
Рис. 2.2. Характеристика мощности (моментно-угловая характеристика) синхронной машины: P, P Т (М, М Т) – мощности (моменты) генератора и турбины
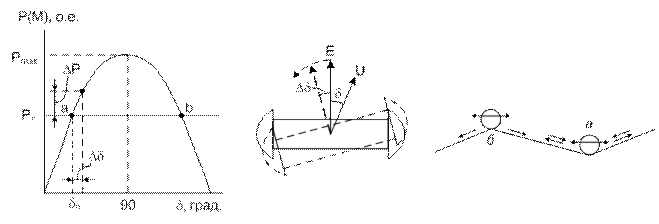
Мощность турбины зависит лишь от количества энергоносителя и в координатах Р,δ изображается прямой линией (рис. 2.2). Заданному значению мощности турбины соответствуют две точки пересечения характеристик турбины и синхронной машины (точки а и b нарис. 2.3, а),в которых мощности генератора и турбины уравновешивают друг друга. Это точки равновесия системы. Рассмотрим режим работы системы в точке а. Допустим, что угол δ получает небольшое приращение Δδ. Мощность генератора, следуя синусоидальной зависимости от угла δ, также изменится на некоторую величину Δ Р, причем положительному приращению угла соответствует положительное приращение мощности (рис. 2.2). В результате изменения мощности генератора равновесие моментов турбины и генератора оказывается нарушенным и на валу машины возникает избыточный момент тормозящего характера, поскольку тормозящий момент генератора преобладает над вращающим моментом турбины. Под влиянием тормозящего момента ротор генератора начинает замедляться, что обусловливает перемещение связанного с ротором вектора ЭДС генератора Е в сторону уменьшения угла δ. В результате уменьшения угла δ вновь восстанавливается исходный режим работы в точке а. Следовательно, режим в точке а будет устойчивым. К аналогичному выводу можно прийти при отрицательном приращении угла δ в точке а.
Рис. 2.3. К определению критерия статической устойчивости: а – моментно-угловая характеристика; б – отклонение вектора ЭДС от состояния равновесия; в – механическая интерпретация устойчивого (а) и неустойчивого (б) равновесия
В точке б положительному приращению угла Dδ соответствует отрицательное приращение мощности генератора D Р. Преобладание момента турбины над моментом генератора обусловит избыточный момент ускоряющего характера, под влиянием которого угол δ начнет возрастать. С ростом угла мощность генератора продолжает падать, что обусловливает дальнейшее увеличение угла δ. Возникает лавинообразный процесс, называемый выпадением из синхронизма. Режим работы в точке б статически неустойчив. Если в точке b угол δ получает отрицательное приращение, на валу машины возникает избыточный момент тормозящего характера, поскольку тормозящий момент генератора преобладает над вращающим моментом турбины. Под действием избыточного момента тормозящего характера рабочая точка системы турбина-генератор переместится в точку а. Таким образом, точка а характеристики мощности является точкой устойчивого равновесия, точка b – точкой неустойчивого равновесия моментов турбины и генератора. Все точки, лежащие на возрастающей части характеристики мощности, являются точками устойчивой работы системы, а точки, лежащие на падающей части характеристики, – точками неустойчивой работы. Границей зон устойчивой и неустойчивой работы является максимум характеристики мощности Механическим аналогом рассматриваемой системы с точки зрения статической устойчивости может служить шарик, помещённый на изогнутую поверхность так, как это показано на рис. 2.3, в. Положение точки а устойчиво, так как любое незначительное перемещение шарика влево или вправо заканчивается его возвращением в исходную точку. Положение b неустойчиво, так как малейшее отклонение от этого положения вызовет переход шарика в новое положение. Из рис. 2.3 видно, что критерием статической устойчивости может служить знак приращения мощности при приращении угла
Полученный признак статической устойчивости носит название практического предела статической устойчивости и формулируется так: если производная электрической мощности по углу положительна, то в данном режиме система статически устойчива. Запас статической устойчивости по мощности определяется как
Запас устойчивости электропередачи, связывающей станцию с шинами энергосистемы, должен быть не менее 20 % в нормальном режиме и 8 % в кратковременном послеаварийном.
|

 а) в)
а) в)
 д)
д)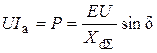 , (2.1)
, (2.1)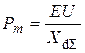 , называемый пределом мощности простейшей электрической системы.
, называемый пределом мощности простейшей электрической системы.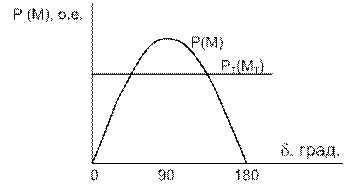
 а) б) в)
а) б) в)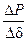 > 0 или, переходя к пределу,
> 0 или, переходя к пределу, 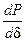 > 0.
> 0.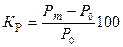 %.
%.


